为了更好地分析电弧的加热作用,这里改变以往把电弧分成两段或三段考虑的传统观点,认为开断电弧对动触头内腔中的气体也有强烈的加热作用。断路器在开断电流过程中,电弧在强烈的气吹作用下,电弧根部弯曲于动触头内部。这里以位于动触头内部一微小段电弧长度lr1作为对Ⅲ部分中气体的热源,以喷口上游一微小段电弧lu作为Ⅱ部分中气体的热源,分别对电弧功率进行分析。......
2025-09-29
对SF6断路器近区故障开断能力进行数值分析,首先应建立开断过程动态数学模型,因为电弧、灭弧室、喷口和动静触头等具有轴对称形状,且以灭弧室中轴线为其对称轴,所建数学模型在空间上为二维轴对称。
1.控制方程
在建立喷口电弧二维数学模型时可以假设如下:
1)电弧等离子体始终满足局部热力学平衡(LTE)条件,可以用统一的热力学温度来描述。
2)忽略等离子体内部的磁场效应以及电极金属蒸气和喷口烧蚀等效应对电弧特性的影响。
这样,圆柱坐标系下电弧数学模型的控制方程可以表述如下:
质量守恒方程为
轴向动量守恒方程为
径向动量守恒方程为
能量守恒方程为
源项为
Q=σE2-Un+Ua
式中 σ、E、Un和Ua——电导率、电位梯度、电弧的辐射功率和吸收功率。
式中 u和V——气流轴向速度和径向速度;
μ=1.550×10-5 N·s/m2,为SF6分子粘性系数。(https://www.chuimin.cn)
另外,补充理想气体状态方程为
p=ρRT (8-79)
和欧姆定律为
以上封闭的偏微分方程组构成了电弧的数学模型。
2.湍流的处理
湍流即在主流流动上叠加无规则的脉动,形成流动中流体间不间断混合或表现为涡流运动。湍流中流体的各种物理参数,如速度、压力、温度等都随时间和空间发生随机的变化。对于管内流动,当雷诺数(Re=pUd/μ)大于2300时,流动一般将从层流状态转化为湍流状态。湍流产生的必要条件是粘性流体中有剪切速度梯度存在。
对双压式灭弧室中SF6气吹电弧的光学测试发现,当电流过零时在电弧等离子体的下游区出现湍流流动,湍流的产生是由于高速流动的等离子体与包裹着它的低速流动的冷气流之间存在着一个较大的速度梯度。
采用K-ε两方程模型来描述湍流效应。确定湍流脉动动能采用K方程,即
式中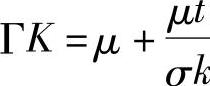 。
。
确定耗散率ε的方程为
式中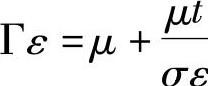 。
。
3.将上述由守恒方程组构成的电弧模型与K-ε方程联立起来构成紊流电弧模型它可以写成矢量形式,即
式中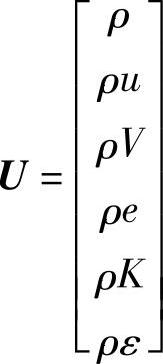 ;
;
下面介绍流体网格法,它是一种气流场数值计算方法。
相关文章

为了更好地分析电弧的加热作用,这里改变以往把电弧分成两段或三段考虑的传统观点,认为开断电弧对动触头内腔中的气体也有强烈的加热作用。断路器在开断电流过程中,电弧在强烈的气吹作用下,电弧根部弯曲于动触头内部。这里以位于动触头内部一微小段电弧长度lr1作为对Ⅲ部分中气体的热源,以喷口上游一微小段电弧lu作为Ⅱ部分中气体的热源,分别对电弧功率进行分析。......
2025-09-29

直流电弧的静态伏安特性是在电弧达到其稳定燃烧状态下得到的。综上所述,在电弧的弧长及电弧散热条件等外界因素不变的情况下,直流电弧的静态伏安特性只有一条,而其动态伏安特性却随着电弧电流Ih变化速度的不同,可能有无数条。......
2025-09-29

游荡型河道是多沙河流最基本的形态之一。最近,作者利用已建立的全动床、不恒定、不平衡和不均匀的水流泥沙数学模型对游荡河道的产生和变化进行了初步的计算研究。并且,在河道变化过程中,游荡河流的一些典型的特性得到展现。在天然河道演变中,控制节点通常是非常重要的因素。......
2025-09-29

简单的尼迈亚模型是一种经验公式类型的电弧数学模型,按图8-1所示,断路器开断过程可分成4个过程,它们是1)瞬动电磁铁动作过程;2)电弧停滞过程;3)电弧运动过程;4)电弧进入电弧栅片熄灭过程。经过停滞阶段后,电弧开始运动,迅速从动触头转移到导弧板,并在磁场力的作用下向栅片运动,计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型,这里介绍尼迈亚模型,它由L.Niemeyer博士于1984年提出[1]。......
2025-09-29

平面二维水流泥沙数学模型有关泥沙部分的主要理论和方法在前面已经有所介绍。数学模型控制方程由水深平均下的浅水方程和泥沙输运方程构成。在小含沙量的条件下,在水中运动的各组粒径的泥沙之间可以认为是相互独立的,在输运方程中可以单独考虑分组泥沙浓度。有关分组挟沙能力或冲刷函数、恢复饱和系数的计算方法已在前面介绍。但是,不恒定模型计算时段较小,处理起来难度相对较小。......
2025-09-29

金属粉芯焊丝有两种类型,一种是适于CO2气体保护焊用的含有一定造渣成分的金属粉焊丝,另一种则是用于富氩保护气体的金属粉焊丝。合适的造渣成分组合使金属粉芯焊丝在CO2气体保护焊条件下获得良好的焊接工艺性。研究金属粉芯焊丝的电弧物理特性有助于加深对金属粉芯焊丝冶金特性和工艺特性的认识,对金属粉芯焊丝产品的研发有现实意义。......
2025-09-29

开关电弧的熄灭,主要是靠对电弧等离子体进行冷却来实现的。电弧等离子体的定压比热容也与固体和液体的情况不同,它是相当复杂的温度函数,随温度的变化,定压比热容有很大的变化。对于断路器中发生的灭弧现象来说,通常考虑在10-6~10-3 s内完成灭弧,因此电弧等离子体在冷却时总是处在游离平衡状态下,电弧等离子体的比热容在游离温度相应处将按Cpe曲线规律变化。......
2025-09-29

在研究都江堰灌区可持续发展状况时,各系统指标体系的选择应注意所研究范围的大小、性质,能满足评价的全面性、代表性要求等。依据综合发展水平,建立可持续协调发展模型,即利用计量经济学中回归分析方法,确定各系统可持续地协调发展的比例关系。进而表明该区域的可持续发展水平,即该区域的发展水平隶属于“可持续发展”的程度。......
2025-09-29
相关推荐