电磁场计算的有限元方法处理过程

2023-07-02 理论教育版权反馈

【摘要】：有限元法计算电磁场的过程中，其步骤如下：1）找出与边值问题相应的泛函及其变分问题。3）求泛函数的极值，导出联立代数方程组，也称为有限元方程。4）用直接法或迭代法计算有限元方程。下面介绍有限元方法的处理过程。图8-40 有限法的场域分割如把场域中所有单元的电位φ按式以各节点电位来表示，则位能X也是φi的函数。

有限元法计算电磁场的过程中，其步骤如下：

1）找出与边值问题相应的泛函及其变分问题。

2）将场域剖分，然后将剖分单元中任意点的未知函数用该剖分单元中形状函数及离散点上的函数值展开，即把连续介质中无限个自由度的问题离散化成有限个自由度的问题。

3）求泛函数的极值，导出联立代数方程组，也称为有限元方程。

4）用直接法或迭代法计算有限元方程。

下面介绍有限元方法的处理过程。

拉普拉斯方程式等效于位能最小原理这点，更一般地可从下面的欧拉原理推导出来。即在某一场域内，如果未知函数φ（x，y，z）满足下列微分方程式：

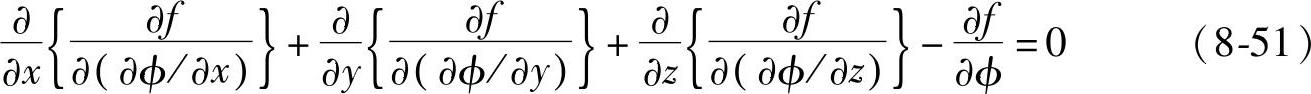
则与下面的积分取最小值完全是等效的：

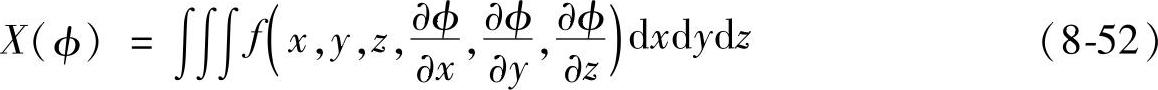
如果把含介电常数ε的场的方程式

div（εgradφ）=0 （8-53）

与式（8-51）相比较，则不难看出对于二维场有

对旋转对称场有

对三维场有

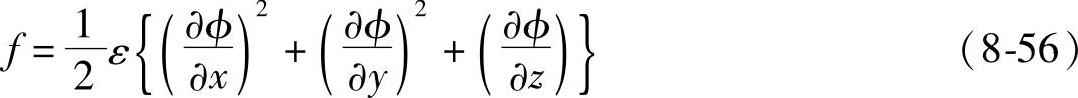
即式（8-53）分别与下列三式取最小是等效：

对二维场有

对旋转对称场有

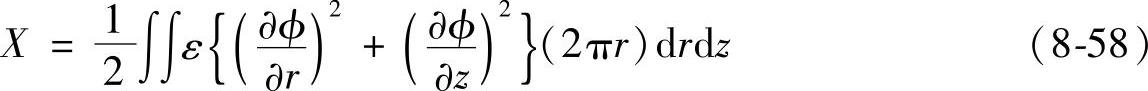
对三维场有

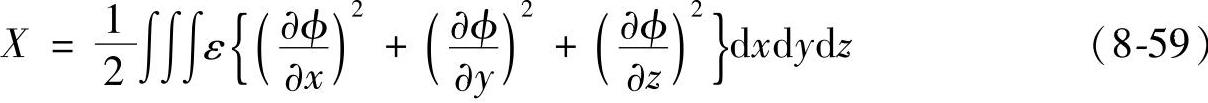
式（8-57）～式（8-59）中的积分项为对应于拉普拉斯方程的泛函。由于X为场域的位能，所以可以说，如果按位能最小来规定电位分布，则它即是所求的静电场。具体的计算步骤如下所述。

现取二维场作为例子，如图8-40所示，把场域按三角形分割，把各三角形单元内的电位φ用坐标x，y的一次式近似表示如下：

φ=a₁+a₂x+a₃y （8-60）

因为电场为-∂φ/∂x，-∂φ/∂y，故式（8-60）的假定是说当单元取得足够小时，在单元内的电场可以看成是不变的，系数a₁～a₃可从三角形单元的3个顶点（把它叫节点）坐标与电位φ_i、φ_j、φ_m（它们是未知量）用下式给出：

从式（8-61）求出a₁～a₃，再代入式（8-60）则有

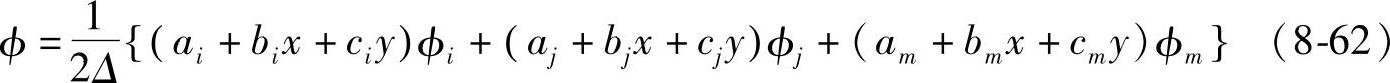
式中 Δ——三角形ijm的面积；

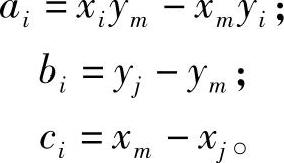
a_i～c_j，am～c_m只要顺次改变i、j、m即可得到。

如用矩阵表示则有

式中N_i=（a_i+b_ix+c_iy）/2Δ；

N_j=（a_j+b_jx+c_jy）/2Δ；

N_m=（a_m+b_mx+c_my）/2Δ。

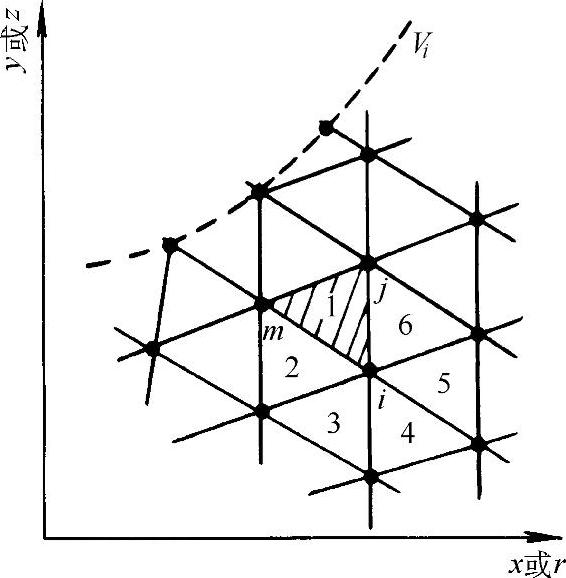
图8-40 有限法的场域分割

如把场域中所有单元的电位φ按式（8-63）以各节点电位（一般取为φ_i）来表示，则位能X也是φ_i的函数。因而，如按X取最小来规定φ_i，则其值是在式（8-60）的假定之下所得出的近似值，如把单元分割得细些，则可期望所得到的值将更接近真正的空间电位。为了把X取为最小值，把节点电位φ_i看作是变量，将对各个φ_i的导数取作零。单元的位能X₁从式（8-57）可得

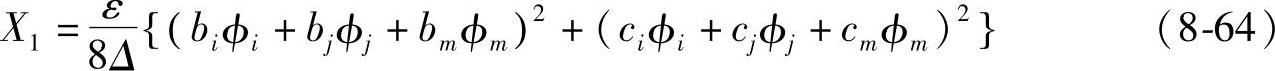
因而整个系统的位能X为

X=∑X_e（场域内的所有单元）（8-65）

如果把X对于φ_i的导数取作零，则如图8-40所示，将只剩下与节点i有关系（包围着）的6个单元，即

如式（8-64）所示，各单元的位能对于节点电位φ_i为二次式。因此，如对φ_i进行微分，可导出对于节点电位（未知数）的一次式。对于所有的节点电位，根据所建立的式（8-66）可得出与未知数的数目相同的多元联立一次方程式。即作为边界条件，如在电极上用所取的节点电位φ_b=V_i，则变为求解与差分式相同的电位方程式的问题，即

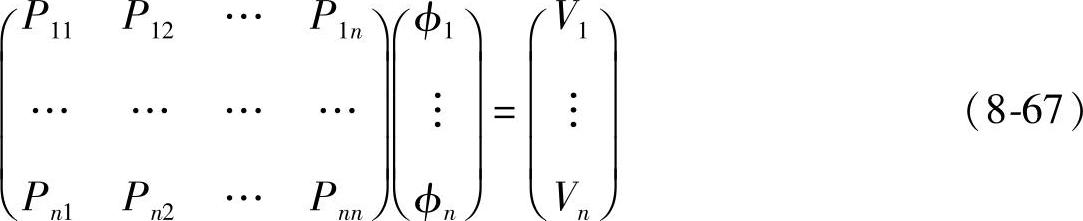
在除去包围i节点的几项外，左边的系数P_ij基本上都是零。另外，在除去与边界有关的项目后右边的系数也基本上是零。

旋转对称场的计算步骤和二维场基本上相同。从式（8-60）～式（8-64），只要取x→r，y→z，则上述式子即可照常使用。但是，在求位能时，式（8-57）和式（8-58）将要出现差别。这是由于对于二维场来说，是把能量密度W进行面积分，而对于旋转对称场来说，则不妨可以看作是进行体积分。由于W与坐标无关，如取Δ为三角形ijm的面积，则有下列关系：

对二维场有

对旋转对称场有

在旋转对称场中，对单元1的位能X₁可采用下式来进行计算：

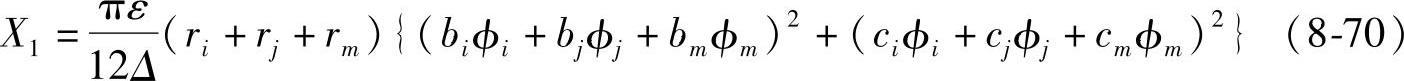
式中的b_i～b_m、c_i～c_m，在式（8-62）中取x→r、y→z即可得出。

电磁场计算的有限元方法处理过程

相关推荐