模拟电荷法：镜像法的推广与应用范围扩大

2023-07-02 理论教育版权反馈

【摘要】：因此，模拟电荷法类似于人们熟悉的镜像法，所不同的是镜像电荷的位置及大小是根据电极表面电位的解析表达式惟一确定的，根据惟一性定理，其解答是惟一的。但它的应用范围大于镜像法，故可将模拟电荷法理解为镜像法的推广。若不符合要求，则重新修正模拟电荷的位置，再行计算，直至达到所要求的精度为止。

1.概念

简单地说，模拟电荷法是在被求的场域以外，用一组虚设的模拟电荷来等效电极表面连续分布的电荷。模拟电荷的位置和形状由人们事先根据电极的形状和对场图的定性分析所假设，而电荷值则由电极的边界条件决定。因此，模拟电荷法的理论根据就是场的惟一性定理。例如在求一对球形电极间的电场（见图8-37）时，可在各个球内设置n个点电荷（q₁，q₂，…，q_n，q′₁，q₂′，…，q_n′），用这2n个离散的电荷代替导球表面存在的连续电荷，而这些模拟电荷值由电极表面给定的电位值决定。因此，模拟电荷法类似于人们熟悉的镜像法，所不同的是镜像电荷的位置及大小是根据电极表面电位的解析表达式惟一确定的，根据惟一性定理，其解答是惟一的。而现在，模拟电荷的值是根据电极表面某些离散点的电位所确定的，当模拟电荷位置不同、电极表面所取的匹配点不同时，解也不同，所以解答不是惟一的，而只是一种近似解。但它的应用范围大于镜像法，故可将模拟电荷法理解为镜像法的推广。当模拟电荷值确定后，场中任意点的电位、场强就由这些集中电荷产生的效应叠加而成。

2.模拟电荷方程组的建立

设有一轴线与地面平行长直圆柱形导体如图8-38所示。欲求圆柱外的电场时，可在圆柱设置n根线电荷（τ₁，τ₂，…，τ_n），它们的位置如图3-38中的·所示；在圆柱导体的表面上取n个匹配点A₁，A₂，…，A_n，如图8-38中的×所示。则各批匹配点上的电位φ₁，φ₂，…，φ_n分别由n根线电荷产生的效应迭加而得，即

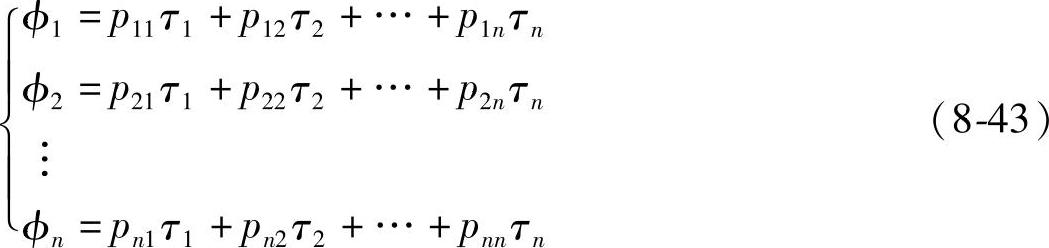
式中p₁₁，p₁₂，…，p_1n——n根线电荷对应于n个匹配点上的电位系数，由线电荷与匹配点之间的相对位置及介电常数决定。式（8-43）可综合成

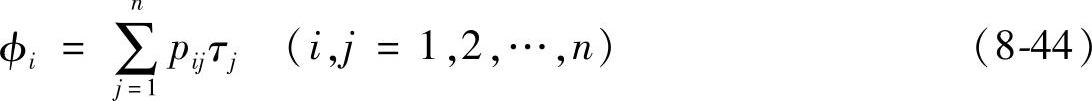
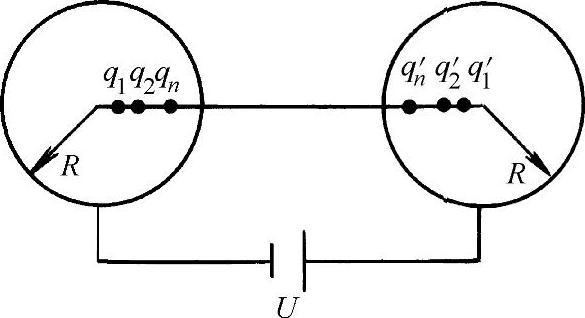
图8-37 一对球形电极间的电场

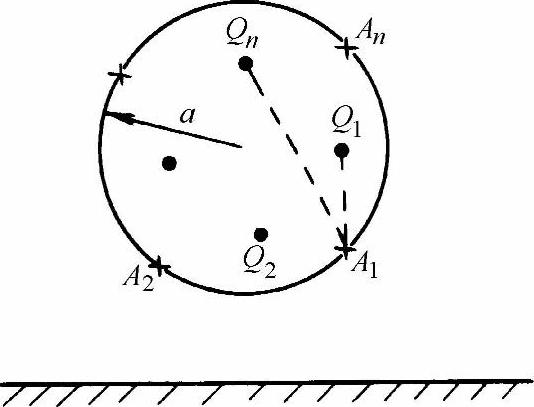
图8-38 一轴线与地面平行长直圆柱形导体

若用矩阵表示则为

[φ]=[p][τ] （8-45）

对于一般情况，式（8-45）中的τ可设为Q，即有

[φ]=[p][Q] （8-46）

式（8-46）中的[φ]、[Q]为n维列向量，为n阶方阵。当模拟电荷类型、位置以及边界上的匹配点选定后，[p]和[φ]均为已知数，以此可求解未知电荷[Q]。

3.模拟电荷方程的求解

根据具体问题列出了代数方程组以后，用高斯列主元消去法即可求解模拟电荷[Q]。然而必须检验这组电荷值是否满足非匹配点处的边界条件。为此在电极表面需另取一些校核点，按

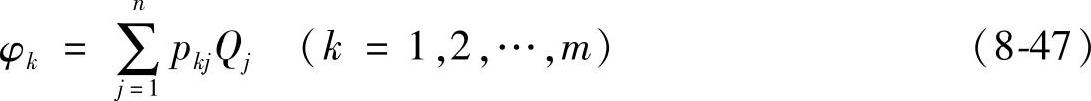
算出这些点上的电位值，将它们与给定的边界电位值φ₀相比，如果两者的差值

|φ_k-φ₀|≤Δ （8-48）

（Δ为预先规定的允许误差），则算得的这组模拟电荷有效，即可用它们来计算场中任意点的电位与场强，若式（8-48）不满足，则应对第一次假设的模拟电荷的位置或个数作适当修正，重新计算[p]及[Q]，直到电位误差|φ_k-φ₀|满足预先给定的精度要求为止。要注意的是，当各模拟电荷的位置相隔很近或匹配点选择不当时，可能出现系数矩阵[p]为病态矩阵的情况。这时可通过适当修正模拟电荷或匹配点的位置来解决。如果要提高数值计算的稳定性及精度，则可用QU分解法及采用双精度型数组求解代数方程组。

4.求场中任意点的电位、场强

当求得满足精度要求的模拟电荷后，场中任意点的电位、场强都可算出，这对计算电场强度非常有利。由于许多高压设备的指标决定于一些点上的最大电场强度值，因此场强的计算在高压电场的计算中十分重要。而模拟电荷法在确定了模拟电荷以后，完全根据解析式求电场强度，所以由此求出的电场强度的误差小于在有限元中确定出的电场强度的误差。

归纳以上所述，可得出模拟电荷法的计算步骤如下：

1）根据对场图的定性分析及经验，设置一组模拟电荷（包括模拟电荷的类型及位置）。

2）根据电极的几何形状，选定足够数量（与模拟电荷个数相等）的匹配点，然后建立系数矩阵[p]。

3）解代数方程组，求出模拟电荷[Q]。

4）在电极表面另取一些点，校核计算精度。若不符合要求，则重新修正模拟电荷的位置，再行计算，直至达到所要求的精度为止。一般经几次修正便能达到要求。

5）按所得的模拟电荷用解析式计算场中任意点的电位和场强。

模拟电荷法：镜像法的推广与应用范围扩大

相关推荐