首页理论教育灭弧室压力特性的数学模型研究

灭弧室压力特性的数学模型研究

2023-07-02 理论教育版权反馈

【摘要】：首先建立灭弧室压力特性的数学模型。将式（8-1）以变化率的形式表示整理得利用式（8-2）分别对图8-31中灭弧室三部分气体列能量平衡方程。总的能量平衡方程可写成如下形式：式中对于Ⅲ部分气体，活塞做功对该部分气体没有直接影响，电弧传递热量为Q3，并且与Ⅱ部分、Ⅰ部分有气体质量交换，总的能量平衡方程可写成如下形式：式中结合理想气体状态方程PV=MRT，可求得三部分气体的压力P、温度T、密度ρ等参数。

首先建立灭弧室压力特性的数学模型。该数学模型有以下三个特点：

1）改变以往将灭弧室中气体参数看作均匀的作法，将灭弧室分成三部分，如图8-31中的Ⅰ、Ⅱ、Ⅲ所示，每一部分作为一个独立系统分析，不仅提高了计算精度，而且有助于分析各参数对灭弧室中气体压力特性的影响程度。

2）根据开断电弧与吹弧气体的相互作用情况及开断电弧所处的位置，把开断电弧分成动触头内部、喷口上游、喷口喉部、喷口下游四部分。

3）计算中，设Ⅰ、Ⅱ、Ⅲ三部分气体为理想气体，忽略各部分摩擦，认为喷口处及各部分之间气体流动为一维等熵流动。

在开断过程中，三部分的热力学参数差别较大，气体状态不完全相同。分成三部分后，每部分气体状态参数近似均匀，可作为集总参数处理。

图8-31 自能式SF₆断路器灭弧室结构简图

1—压气室 2—膨胀室 3—动触头 4—气缸 5—喷口 6—静触头

A—动触头排气孔

三部分中的任意一部分都是变质量系统，变质量系统的热力学第一定律表达式如下：

δQ+∑eδm=dE+δW （8-1）

式中 δQ——电弧传递给系统的热量微元；

∑eδm——由于系统与外部气体质量交换而带进系统的能量之和（其中e=h，h为气体的焓）；

dE——该系统储存能微元，只考虑其内能，故E=C_vMT（C_v为SF₆气体定容比热，M为系统气体质量，T为系统气体温度）；

δW——该系统对外做功微元。

将式（8-1）以变化率的形式表示整理得

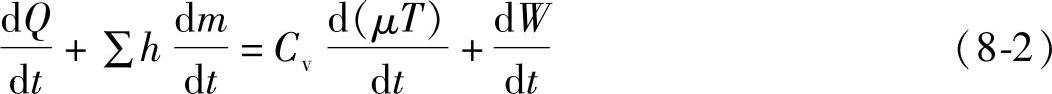
利用式（8-2）分别对图8-31中灭弧室三部分气体列能量平衡方程。并规定三部分气体分别用下角1、2、3表示。灭弧室外部的气体用下角0表示，质量流率的双下标中，前一数字代表质量流出的系统，后一数字代表质量流入的系统。

对于Ⅰ部分气体，电弧对该部分气体没有直接影响，故dQ/dt=0。活塞对此部分气体做功，故dW/dt=p₁A_v。当排气孔位于活塞内侧时，Ⅰ、Ⅱ、Ⅲ相互之间有气体质量交换，当排气孔位于活塞外侧时，只有Ⅰ、Ⅱ部分之间有气体质量交换。总的能量平衡方程可写成如下形式：

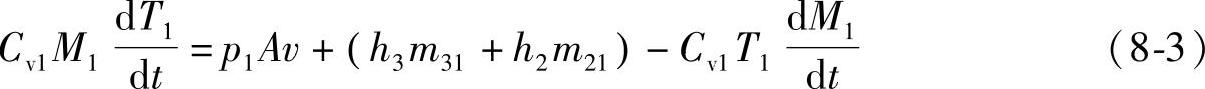
式中 A——活塞面积；

v——触头打开速度；

p₁——Ⅰ部分气体的压强；

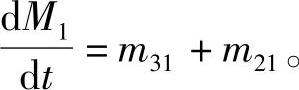
对于Ⅱ部分气体，活塞做功对该部分气体没有直接影响，故dW/dt=0，电弧传递的热量为Q₂，该部分气体与Ⅰ、Ⅲ部分质量交换的同时，在喷口打开后，向灭弧室外部泄漏气体。总的能量平衡方程可写成如下形式：

式中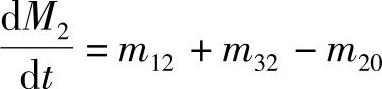

对于Ⅲ部分气体，活塞做功对该部分气体没有直接影响，电弧传递热量为Q₃，并且与Ⅱ部分、Ⅰ部分（或灭弧外部，与排气孔位置有关）有气体质量交换，总的能量平衡方程可写成如下形式：

式中

结合理想气体状态方程PV=MRT，可求得三部分气体的压力P、温度T、密度ρ等参数。