探究交流电弧对电路的影响：具有电弧的交流电路

2023-07-02 理论教育版权反馈

【摘要】：按上述假定，则式可改写为在电流正半周内将上式直接积分，得由此式可见，电弧电流ih可简化为由两个分量组成：一个是滞后于电压90°的正弦电流分量；另一个是随时间线性变化的分量。电弧电压所起的影响表现在第二个电流分量上，Uh愈大，则分量i″也愈大，电弧电流发生的畸变也愈大。

图6-11示出具有电弧的交流电路，电路中的电阻R、电感L触头两端的电容C均为线性元件，电弧可以用一非线性的电弧电阻R_h来表示，令电源电压u=E_mcosωt，可得电弧燃烧时的电路方程式为

图6-11 具有电弧的交流电路

通常触头两端的电容C很小，因此在电弧电压变化不大的情况下，电容电流i_c可以略去，此时电路中电流i就等于电弧电流i_h，而有

由于R_h是一个可变的非线性参数，只要存在电弧电压，电流就不会按正弦规律变化。

为了清楚地看到电弧的影响，可再作如下的一些简化假定：

1）由于通常在电感电路中，电阻R很小，可将R略去；

2）以电流过零时为计时起点，此时电源电压为最大值；

3）当t=α/ω时触头分离，电弧燃烧，α为起燃相位角；

4）电弧电压|u_h|=U_h（常数），并随电流改变正负号。

按上述假定，则式（6-32）可改写为

在电流正半周内将上式直接积分，得

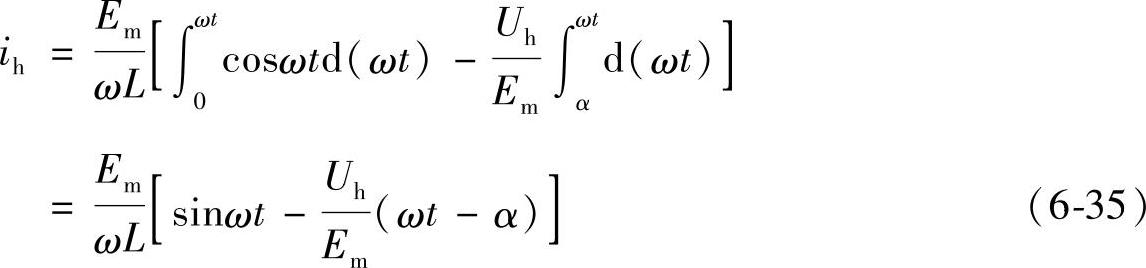
由此式可见，电弧电流i_h可简化为由两个分量组成：一个是滞后于电压90°的正弦电流分量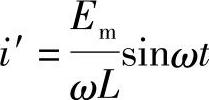；另一个是随时间线性变化的分量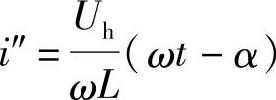。电弧电压所起的影响表现在第二个电流分量上，U_h愈大，则分量i″也愈大，电弧电流发生的畸变也愈大。其曲线关系如图6-12所示。

半周后电弧电流要过零，过零的时间t₁可令i_h=0。从式（6-35）求得

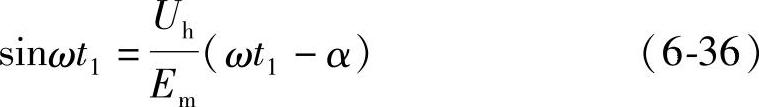
t₁也可用作图法求得，从图6-12中可看出，电流的正弦分量曲线i′和直线分量i″的交点所对应的时刻即为电弧电流过零时刻t₁。不难看到，电弧电流的实际过零点早于正弦分量的电流零点——电流的自然零点。也就是说，电弧电流不仅波形发生畸变，而且过零的时间也发生了变化，出现了电弧电流零点比电流自然零点提前现象。图中ξ就是提前过零的相位角，因为ξ=π-ωt₁，所以有

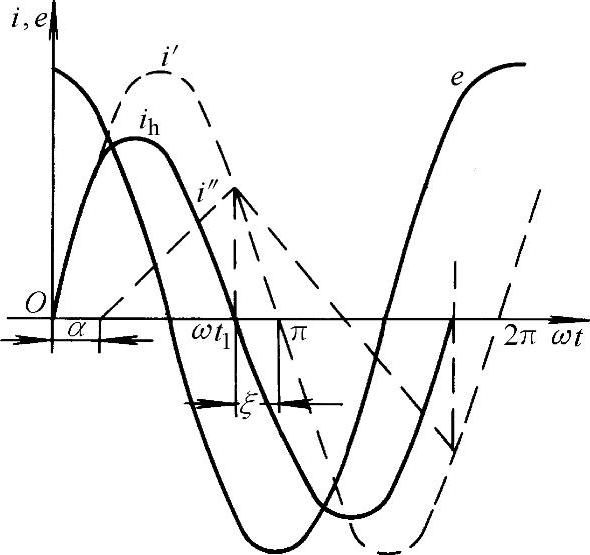
图6-12 电弧电流的变化曲线

按式（6-37）用作图法求得的ξ与起燃相位角α的关系，如图6-13所示。U_h/E_m的值越大，则ξ越大，电弧电流过零提前越早。

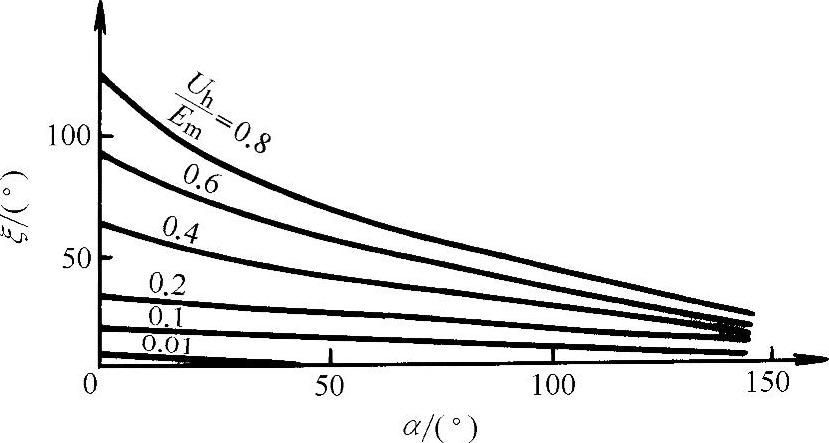
图6-13 ξ与α的关系

若电流过零后，电弧又立即燃烧，电流和电压均同时反向，则可对第二个半周再作分段积分，从而得到第二个半周电弧的情况。同样，对于其他电弧电压不为常数的情况，只要能写出近似表达式，例如电弧电压随时间线性增长，也可用类似方法加以分析，不再在这里详述。

当电弧电压很小以致可以忽略不计时，由于电弧电流中的线性变化分量i″=0，此时电弧电流可被近似地看作按正弦变化，即

可见电弧的存在将使电路的分析变得困难。考虑到在电流足够大，弧隙游离程度足够高时，电弧电阻很小，对电路影响不大，此时可略去电弧电阻，把电弧近似地看成是一个短接的导体。而电弧一旦熄灭，触头间隙能很快变成气体介质，则可假设间隙的电阻立即趋于无限大。这种在燃弧时电弧电阻为零，熄弧后电阻立即变成无限大的电弧称为理想电弧。为了分析上的方便，在某些情况下可近似地用理想电弧来取代实际电弧。显然，理想电弧的电流零点将与电流自然零点重合。

探究交流电弧对电路的影响：具有电弧的交流电路

相关推荐