2）计算模型采用Midas Civil 软件进行整体结构受力分析。图3-6直沽桥空间计算模型3）静力分析进行全桥静力分析，考虑结构自重、车辆荷载、人群荷载、风荷载、整体升降温、局部温差以及各个墩位6 mm 的不均匀沉降等工况。分析结果表明，直沽桥主体结构设计满足抗震规范要求。计算结果表明，结构在恒载、满布汽车和人群荷载作用下，最小屈曲临界荷载系数为5.45，满足规范要求。......
2023-07-01
整体计算分析技巧与步骤
【摘要】：图6-17空间计算模型主缆在施工初期的空缆状态为一悬链线。主缆轴力最大值为26 800 kN，吊杆轴力最大值为2 000 kN。
富民桥为自锚式悬索桥，锚固形式独特：主跨自锚，边跨地锚。缆索体系独特：主塔位于道路中线，边跨缆索过主塔直接锚固于地锚，主跨缆索过主塔分别向外自锚在另一端主梁两侧，吊杆自主梁外侧与缆索相连，在吊杆拉力作用下，形成空间缆索。由于富民桥采用空间缆索体系和主跨自锚边跨地锚的桥梁结构形式，使得主桥结构的主缆合理初始索力、全桥静力特性和地震响应均具有其自身的特点。
6.2.3.1 主要规范及标准
（1）《公路桥涵钢结构及木结构设计规范》（JTJ 025—1986）。
（2）《城市桥梁设计准则》（CJJ 11—1993）。
（3）《城市桥梁设计荷载标准》（CJJ 77—1998）。
（4）《公路桥涵设计通用规范》（JTG D60—2004）。
（5）《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）。
（6）《公路桥涵地基与基础设计规范》（JTJ 024—1985）。
（7）《公路工程抗震设计规范》（JTJ 004—1989）。
6.2.3.2 主缆初张力的确定
采用有限元分析软件建立富民桥计算模型，其中，缆索和吊杆采用索单元模拟，主梁和塔采用梁单元模拟。全桥共625 个节点，944 个单元。空间计算模型如图6-17 所示。
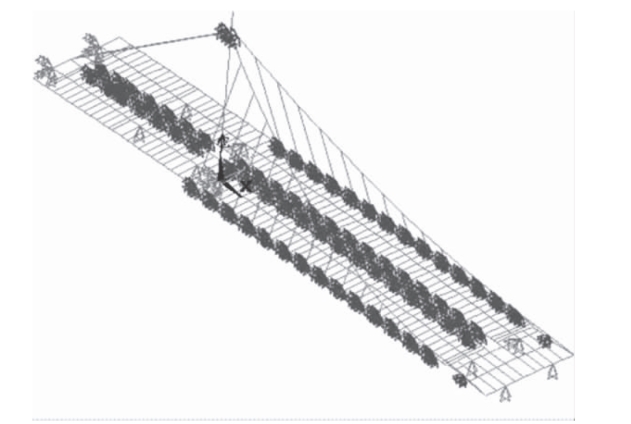
图6-17 空间计算模型
主缆在施工初期的空缆状态为一悬链线。缆索初张力的选择要综合考虑缆索的抗拉强度、锚碇和散索套的应力集中、整体结构刚度的分配、钢加劲梁的受力和成桥缆索转换的施工难度等多种因素，找到一个最优的平衡状态。空间缆索在成桥的过程中，在不同的初张力作用下，竖、横、纵三向变位不同，对吊杆索力、主鞍位置、成桥状态的受力性能也有影响。
1）全桥整体结构安全
主缆初张力的大小对成桥状态的受力性能有一定影响，但差异不大。主缆初张力较小时，成桥状态对活荷载的承受性能相对好一些。
2）主鞍、锚碇、散索套等构件
主缆初张力的大小对成桥状态主缆在主鞍位置的入角有较明显的影响，对主塔在施工初期的偏位也有一定影响，但主塔偏位可以通过后续的施工方法予以消除。主缆初张力小，成桥后缆索的拉力小，利于主鞍、锚碇和散索套等构件的设计。
3）吊杆
主缆初张力的大小对成桥时吊杆力的大小及分布没有明显影响，只要通过合理的调索方法，最终成桥时的吊杆力大小及分布基本一致。
根据初步计算分析，选择3 个主缆空缆状态的初张力，其中包括主缆空缆初张力1 710 kN（可以实现主缆牵引入散索套）、主缆空缆初张力17 130 kN（空载线形基本达到稳定状态）、主缆空缆初张力30 300 kN（成桥时主缆应力达到安全极限）进行计算分析。主缆自空缆至成桥状态的线形变化、塔顶位移、主梁应力和挠度等数据是对各部位构件控制的重要参数，作为主要对比指标。考虑到在施工中主缆处于空缆状态时，主缆初张拉越小，在主鞍及散索套出口位置的转角作用越小，更方便施工，且对于锚碇、索鞍、散索套和缆索等构件更容易实现，最终确定采用1 710 kN 的初张力。主缆空缆初张力为1 710 kN 时，主缆由空缆状态到成桥状态坐标及位移值列于表6-1。
表6-1 主缆空缆初张力为1 710 kN时，主缆空缆至成桥线形坐标 （m）
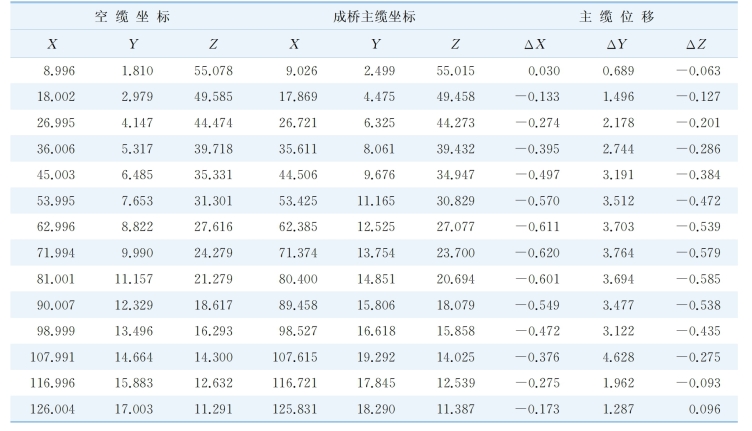
注：坐标自主塔向主跨顺桥向为X 向，横桥向为Y 向，竖直向为Z 向
主缆空缆初张力为1 710 kN 时，吊杆及主缆成桥内力列于表6 -2。
表6-2 吊杆及主缆成桥内力 （kN）
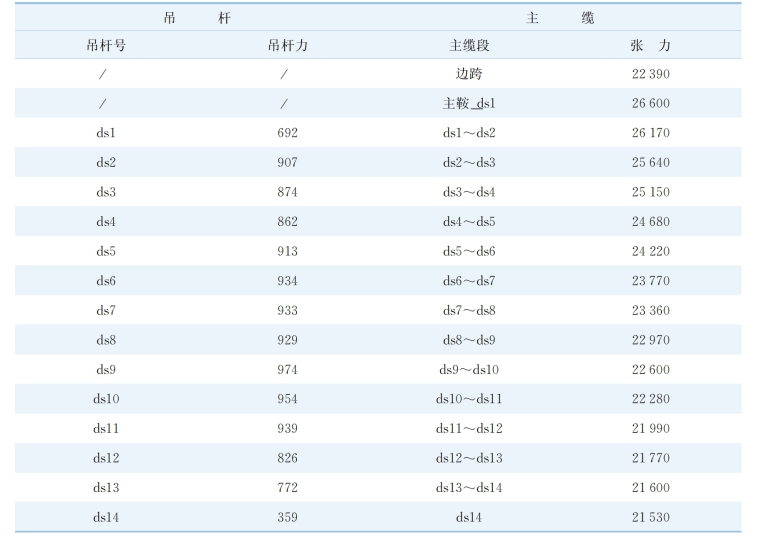
主缆空缆初张力为1 710 kN 时，主缆由空缆状态到成桥状态变形立面、平面、断面如图6 -18～6- 20 所示。
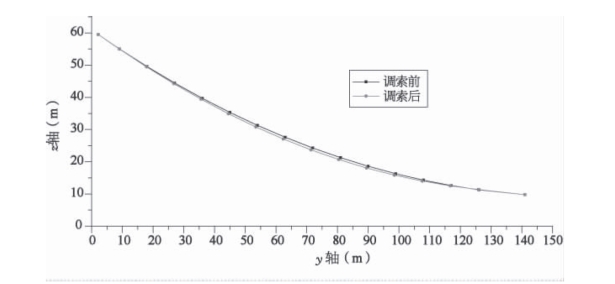
图6-18 空缆至成桥状态主缆变形立面投影
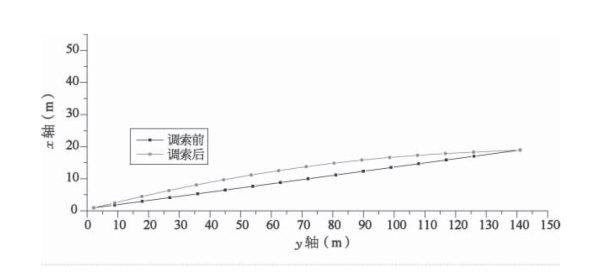
图6-19 空缆至成桥状态主缆变形平面投影
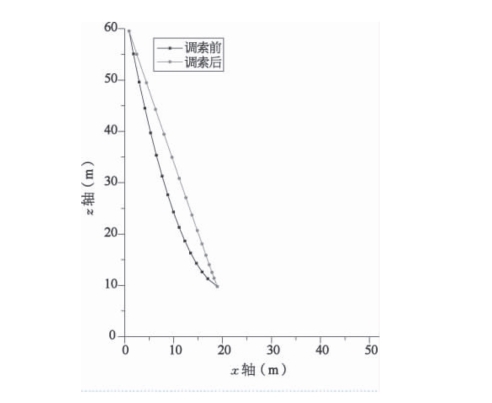
图6-20 空缆至成桥状态主缆变形断面投影
调索后，主梁钢结构底板的应力与挠度列于表6 -3。
表6-3 主梁结构底板的应力与挠度
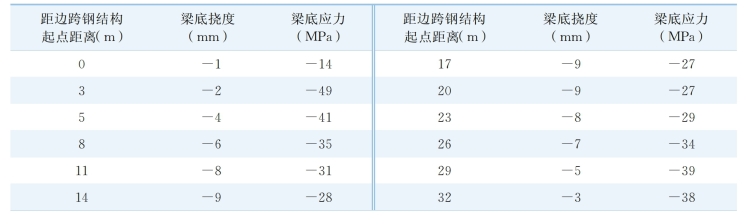
（续表）
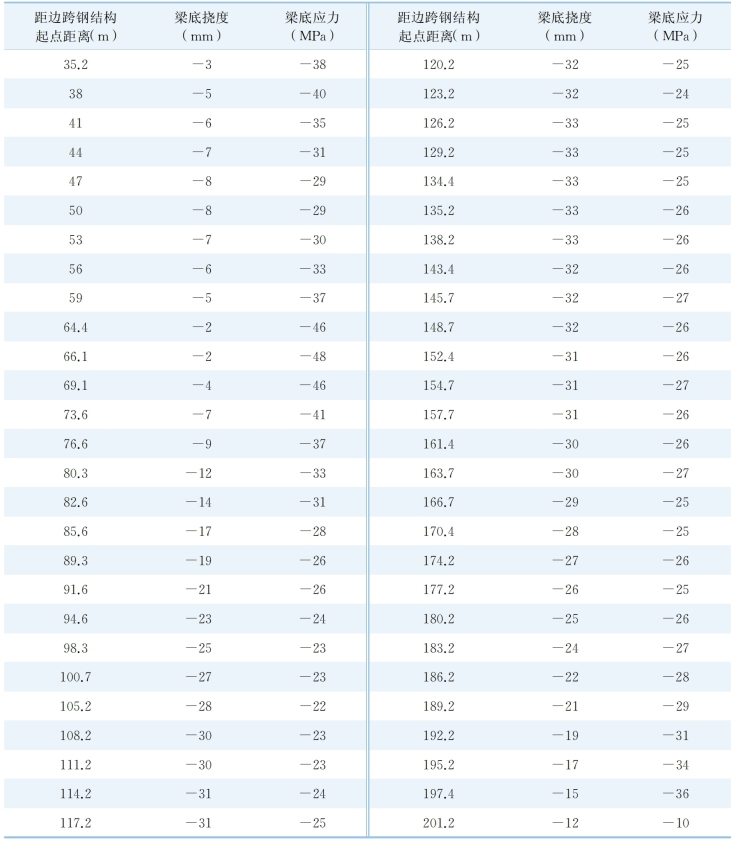
设计主缆梁端初张力为1 710 kN，在调索进行体系转换后，梁端主缆张力达到21 530 kN，塔端主缆张力为26 600 kN，边跨主缆张力为22 390 kN；吊杆索力均值为85 kN；索吊点梁的挠度为0.033 m；塔顶向主跨位移为0.097 m；梁底钢结构顺桥向应力为6～-75 MPa。
桥梁在运营阶段主要承受城-A 级荷载，主缆初张力为1 710 kN 时，在城-A 级荷载作用下，结构体系产生的挠度值、应力值分别见表6 -4。
表6-4 主缆初张力1 710 kN 结构在城-A 级荷载作用下的挠度与应力
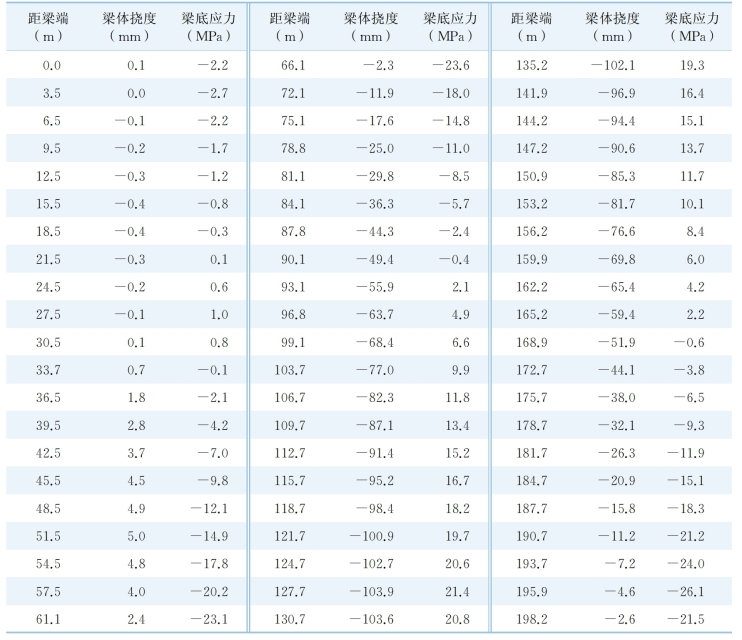
由上表可知，主缆空缆初张力为1 710 kN 时，在城- A 活载作用下，结构最大挠度为104 mm，主跨最大应力为21 MPa。
6.2.3.3 静力分析
1）荷载及荷载组合
永久作用包括结构一期和二期重力、混凝土收缩及徐变作用、预应力作用、基础沉降等。可变作用主要是城-A 荷载，由于车辆作用布置的不确定性，对结构各部位均有不同的最不利荷载布置。因此，应按多种布置进行计算并取包络结果。具体布置包括上行桥满布、下行桥满布、全桥满布、主跨满布、边跨满布汽车车道荷载。
在设计中考虑如下几种荷载组合：
组合1：永久作用。
组合2：永久作用+上行桥满布等效汽车静载。
组合3：永久作用+下行桥满布等效汽车静载。
组合4：永久作用+全桥满布等效汽车静载。
组合5：永久作用+主跨满布等效汽车静载。
组合6：永久作用+边跨满布等效汽车静载。
2）静力计算结果
组合1：永久作用
静力分析得到的结果包括主缆位移、主缆轴力、吊杆拉力，如图6-21 所示。
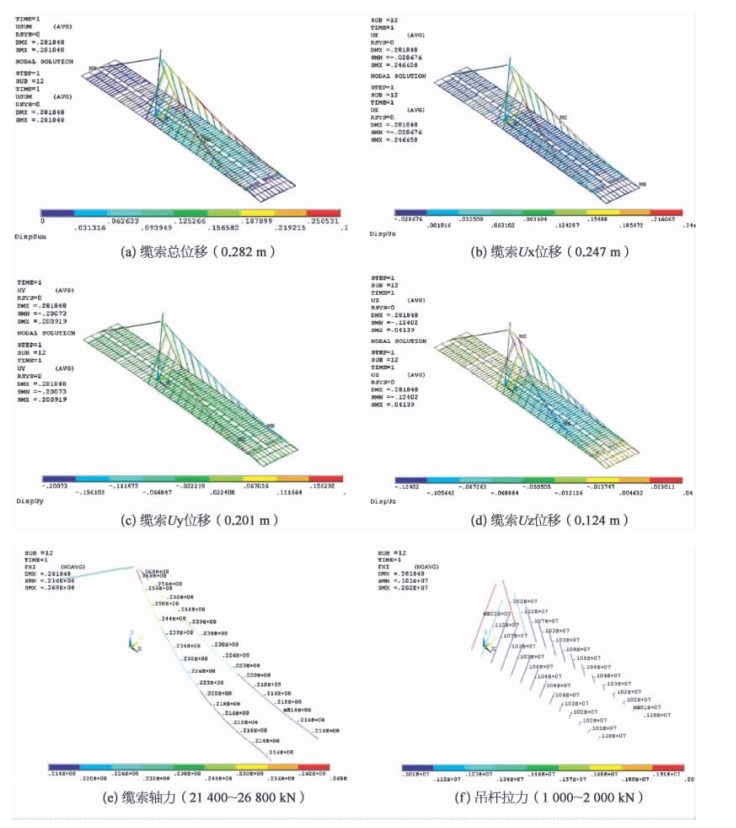
图6-21 组合1 作用下缆索系统位移及内力
主缆在施工过程的位移已经完成，上图中，在二期恒载作用下产生，最大位移值为0.282 m，顺桥向位移为0.247 m，横桥向位移为0.201 m，竖直向位移为0.124 m。主缆轴力最大值为26 800 kN，吊杆轴力最大值为2 000 kN。
组合2：永久作用+上行桥满布等效汽车静载
在组合2 作用下，主缆位移、主缆轴力、吊杆拉力如下。
在荷载组合2作用下，主缆最大位移值为0.310 m，顺桥向位移为0.246 m，横桥向位移为0.201 m，竖直向位移为0.215 m。主缆轴力最大值为27 100 kN，吊杆轴力最大值为2 100 kN。
组合3：永久作用+下行桥满布等效汽车静载
在组合3 作用下，主缆位移、主缆轴力、吊杆拉力如下。
在荷载组合3 作用下，主缆最大位移值为0.310 m，顺桥向位移为0.246 m，横桥向位移为0.201 m，竖直向位移为0.215 m。主缆轴力最大值为27 100 kN，吊杆轴力最大值为2 100 kN。
组合4：永久作用+全桥满布等效汽车静载
在组合4 作用下，主缆位移、主缆轴力、吊杆拉力如下。
在荷载组合4 作用下，主缆最大位移值为0.304 m，顺桥向位移为0.218 m，横桥向位移为0.198 m，竖直向位移为0.201 m。主缆轴力最大值为27 000 kN，吊杆轴力最大值为2 080 kN。
组合5：永久作用+主跨满布等效汽车静载
在组合5 作用下，主缆位移、主缆轴力、吊杆拉力如下。
在荷载组合5 作用下，主缆最大位移值为0.313 m，顺桥向位移为0.211 m，横桥向位移为0.197 m，竖直向位移为0.221 m。主缆轴力最大值为27 000 kN，吊杆轴力最大值为2 080 kN。
组合6：永久作用+边跨满布等效汽车静载。
在组合6 作用下，主缆位移、主缆轴力、吊杆拉力如下。
在荷载组合6 作用下，主缆最大位移值为0.247 m，顺桥向位移为0.247 m，横桥向位移为0.201 m，竖直向位移为0.201 m。主缆轴力最大值为26 800 kN，吊杆轴力最大值为2 020 kN。
结合各作用组合结果可知，城-A 车道作用的不同布置对主缆的位移、内力及吊杆力影响差异不大，结构均处在安全范围内。
6.2.3.4 抗震性能分析
1）主桥动力特性分析
振动模态是弹性结构的固有特性，本桥前10 阶自振频率见表6-5。
表6-5 本桥前10 阶自振频率
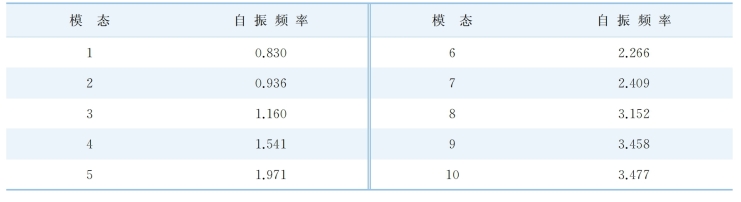
结构前5 阶振动模态如图6-22 所示。
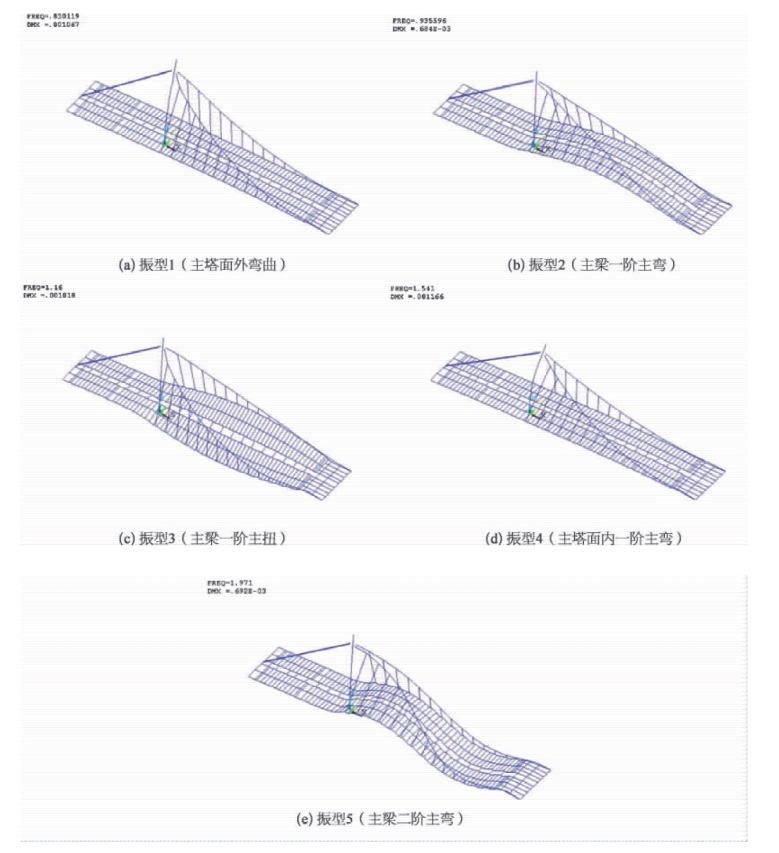
图6-22 结构前5 阶振动模态
2）时程分析结果
时程分析采用天津波，持续时间为12 s，时间间隔为0.02 s，峰值加速度为1.458 m/s2。时程计算部分结果如图6 -23～图6 - 25 所示。
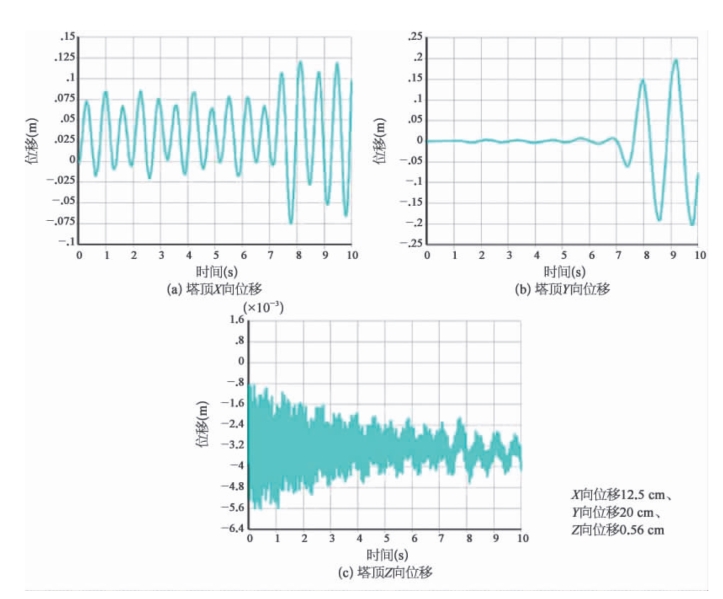
图6-23 地震作用下塔顶位移
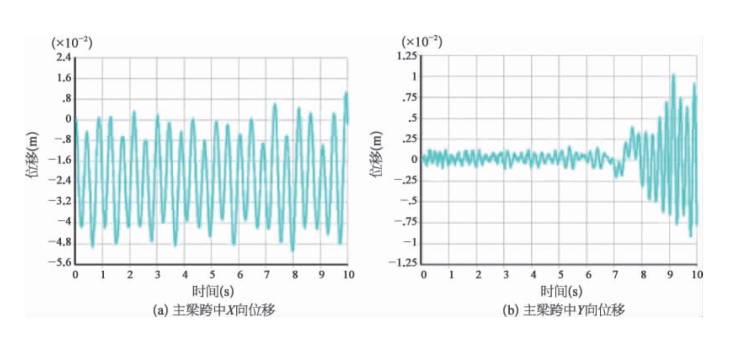
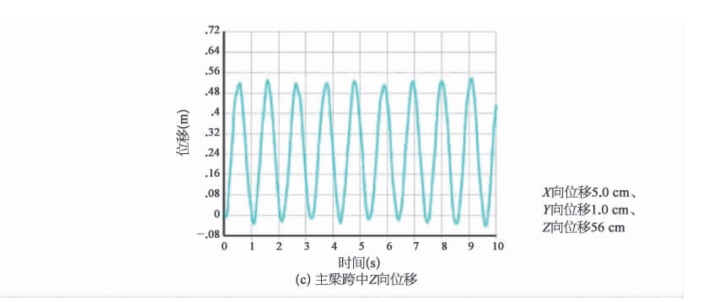
图6-24 地震作用下主梁跨中位移
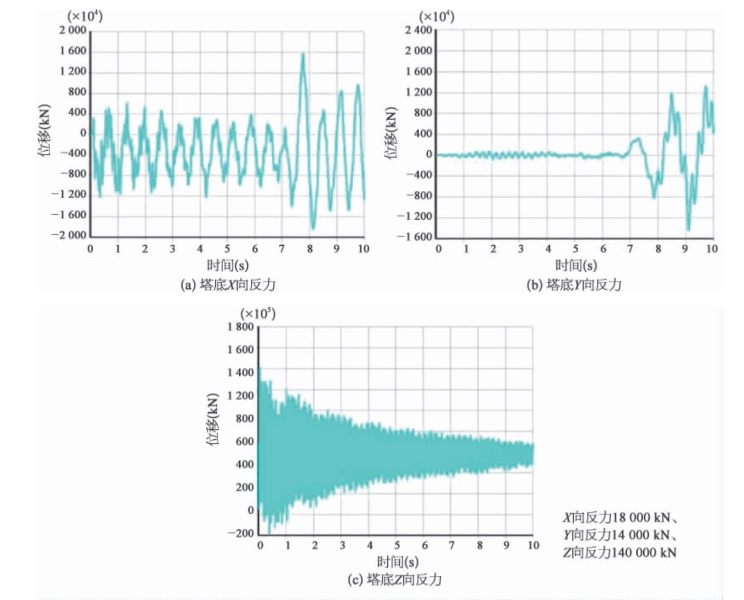
图6-25 地震作用下塔底反力
地震作用下主塔、主梁最大位移及内力如下：塔顶X 向（顺桥向）位移为12.5 cm，塔顶Y 向（横桥向）位移为20 cm，塔顶Z 向（竖向）位移为0.56 cm。主梁跨中X 向位移为5.0 cm，主梁跨中Y向位移为1.0 cm，主梁跨中Z 向位移为56 cm。塔底X 向反力为18 000 kN，塔底Y 向反力为14 000 kN，塔底Z 向反力为140 000 kN。依据桥梁抗震分析计算结果，进行下部结构的抗震性能验算。结果表明，主桥结构抗震性能满足规范要求。
有关城市桥梁设计创新与实践的文章
- 详细阅读
- 详细阅读
-
整体计算分析：考虑全局视角详细阅读
2）计算模型采用大型有限元分析软件Midas Civil 进行全桥上部结构整体计算分析。4）静力分析结果大沽桥钢结构采用容许应力法设计，经计算，标准作用组合下，大沽桥大拱最大应力为151 MPa，小拱最大应力为154 MPa，主梁最大应力为110 MPa，满足规范要求。表2-1前10 阶屈曲临界荷载系数图2-15一阶屈曲失稳模态6）抗震性能分析结果采用反应谱分析方法对大沽桥进行抗震性能分析。分析结果表明，大沽桥抗震性能良好，主体结构满足规范要求。......
2023-07-01
-
整体计算分析方法探析详细阅读
1）静力分析通过对上部结构进行整体计算分析可知，恒载作用下，主桥钢箱梁应力在- 105～72 MPa，纵拱应力在-116～60 MPa，横拱应力在- 79～97 MPa。组合Ⅰ作用下，箱梁应力在- 163 ～109 MPa，纵拱应力在-164～106 MPa，横拱应力在-173～169 MPa，桥梁各部位应力符合规范要求。图4-23屈曲分析活载加载工况表4-6各工况前6 阶模态临界荷载系数图4-24满布活载工况桥梁第3 阶屈曲模态......
2023-07-01
-
整体计算分析：探索有效切入点优化业务策略详细阅读
图7-14组合桁梁桥全杆系模型7.2.3.2施工阶段定义为了更有效地改善连续组合桁梁桥负弯矩区的受力性能，该桥综合采用部分组合技术、双重组合技术以及优化施工工序三项措施。表7-1模型计算中定义的施工阶段情况7.2.3.3施工阶段分析分析得到桥梁各个施工阶段的计算结果，所有的荷载效应及组合均按照《公路桥涵设计通用规范》选取。......
2023-07-01
-
计算直线相邻点的方法与步骤详细阅读
4）直线相邻点：在图6.4-1中选择点计算4，计算的是指定直线上与基准点距离最近的点（垂足），直线应通过点和角度确定，需要输入的数据为基准点的X/Y坐标、直线上某一点的坐标U/V、直线与X轴的夹角A、直线的偏移距离D和偏移方向DIRC。......
2023-06-25
-
读图的基本步骤与技巧详细阅读
读图一般以形体分析法为主，线面分析法为辅，这两种方法在读图过程中不能截然分开，根据不同的组合体，灵活运用。一般的读图步骤可分为以下四步。对如图8-22所示的组合体进行分析。下面再分析第二个线框，通过“三等”对应关系分析，得到如图8-26所示的加粗和加阴影部分。图8-26组合体中的正面投影中第二个线框的分析根据投影规律分析，这是一个正平面。......
2023-06-22
-
PLC系统调试技巧与步骤详细阅读
若通过逐段检查无异常，则可使用万用表检查连接的PLC系统线路有无短路、断路以及接地不良等现象，若出现连接故障应及时对其进行连接或调整。图13-58 PLC扩展接口的连接......
2023-06-24
相关推荐