根据二者之间的结构和受力关系，可将站房划分为如下4 类：桥式站房桥式站房的受力以桥墩为主，即车站建在一组桥墩上，一般为桥下式站房，如图6.1 所示。建式站房建式站房也称楼式站房，与桥式站房不同，其结构受力主要依靠站房的柱子和墙体。这种结构形式也称为房桥分离、桥建分离。我国目前特大型车站较多采用该种结构体系。图6.1桥式站房图6.2建式站房图6.3桥建分离图6.4桥建合一......
2023-08-21
结构受力优化分析
【摘要】：图4-18空间计算模型基于金阜桥结构受力的复杂性，从方案设计阶段至施工图设计阶段均应进行结构设计优化。表4-1V 形墩、撑杆及斜撑设置效应对比由以上计算结果可知，通过设置V 形墩、斜撑和撑杆等支撑构件，可大大改善桥梁结构的受力状态，这是十分必要的。
金阜桥为非对称的空间梁拱组合结构体系，设计施工难度大。采用Midas Civil 软件，重点进行桥梁整体结构的三维线性分析。采用梁格法将主桥的正交异性板梁体离散为纵梁和横梁体系。纵、横拱及挑梁网状格构和辅桥梁体采用与实际布置情况一致的梁格进行模拟，尤其是对于纵拱和横拱拱条单元，加密单元划分的密度以模拟其三维空间变化曲线，采用变化的β角模拟纵拱不断变化的扭转效果。撑杆、斜撑、V形墩（钢结构）采用梁单元模拟，同时在斜撑底部与混凝土系梁单元连接，并释放弯曲和扭转自由度，以消除附加弯矩和扭矩对局部受力的不利影响，V 形墩（钢结构）下模拟出5 m高的混凝土墩柱，以考虑其对整体结构的影响，V形墩（钢结构）下端点与V形墩（混凝土）上端点采用横桥向与竖直方向的刚性连接。考虑横拱与主桥边梁L1、辅桥纵梁L2 及相关纵拱连接点实际构造造成的连接位置的差异影响，并进行必要的刚性连接。空间计算模型如图4-18 所示。
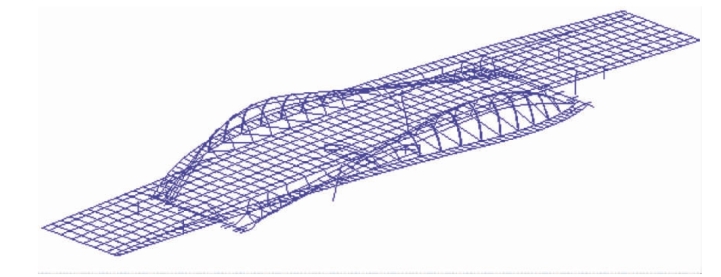
图4-18 空间计算模型
基于金阜桥结构受力的复杂性，从方案设计阶段至施工图设计阶段均应进行结构设计优化。从结构主要受力构件的布置、结构及构件约束条件的选取，构件截面形式及尺寸的确定乃至结构特殊部位构造的处理，逐步掌握该特殊桥型结构的受力特点与规律，应用比较妥当可靠的构造处理方式，使实际受力情况与理论计算尽量吻合一致，更好地指导后续结构设计与桥梁施工。
4.2.3.1 支撑构件的设置研究
如上所述，金阜桥上部结构由撑杆、斜撑和V 形墩共同支撑。支撑杆件的设置，对于改善结构局部乃至整体受力情况都是十分重要的。分别对无V 形墩、无斜撑与撑杆以及有V 形墩、斜撑和撑杆支撑的结构进行计算，结构相应变形状态及应力分布等情况见表4 -1。
表4-1 V 形墩、撑杆及斜撑设置效应对比
由以上计算结果可知，通过设置V 形墩、斜撑和撑杆等支撑构件，可大大改善桥梁结构的受力状态，这是十分必要的。
4.2.3.2 约束布置优化研究
1）3#、4#墩位约束优化
针对3#、4#墩位V形墩下端的约束情况进行如下优化比较：①约束顺桥向和竖直方向（标识为Dx、Dz）；②约束顺桥向、横桥向和竖直方向（标识为Dx、Dy、Dz）；③约束顺桥向、横桥向、竖直方向及三个方向的转动（标识为Dx、Dy、Dz、Rx、Ry、Rz）；④约束顺桥向和竖直方向（标识为Dy、Dz）。
获得各种约束情况下的V形墩和结构整体组合应力分布以及支座反力分布情况，并进行比较，得出如下结论：对V形墩下端分别采用以上4种约束方式进行比较分析，相比于前3 种，第4 种约束方式对V形墩及其相应横梁乃至整体结构的应力水平均具有一定改善作用，仅恒载作用下V形墩及相应横梁的应力即得到很大改善，最大可达20 MPa，同时使主桥其他部位的应力分布更为均匀（拉压应力水平趋于接近）。另外，在温度荷载作用下，前3 种约束情况由于V 形墩下端顺桥向的滑动受到限制，导致其温度应力较大（-24～24 MPa）；而在第4 种约束情况下温度应力只有-9～9 MPa。由于V形墩及附近区域是全桥受力的关键部位，采用最优的约束方式对于控制其应力水平效果显著。综合以上分析结果，最终确定在3#、4#墩位V形墩下端采用第4 种约束方式，即约束横桥向和竖直方向。
2）斜撑下端铰接优化
斜撑下端点与混凝土系梁采用刚性连接方式，将导致斜撑下端承受很大的弯矩作用，进而使斜撑下端的应力水平非常高。为了减小斜撑下部承受的弯矩，斜撑采用上大下小的截面形式，仅恒载作用下其组合应力已达300 MPa。通过释放斜撑下端的弯曲和转动自由度（即仅平动方向与混凝土系梁连接），进而减小附加弯矩的影响，对于改善斜撑构件的局部受力效果十分明显。计算结果表明，释放转动约束，恒载作用下斜撑组合应力仅为-76 MPa，同时对其他部位基本没有影响。因此，最终采用盆式固定支座实现斜撑下端与混凝土系梁的连接，以确保实际构造与计算模拟方法吻合一致。优化后的斜撑下端约束布置形式如图4 -19 所示。
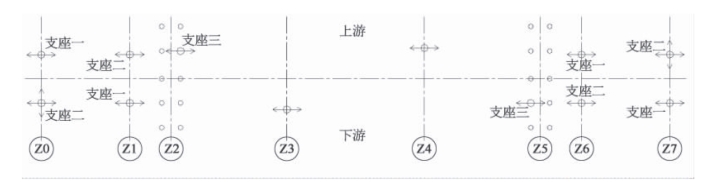
图4-19 优化后的斜撑下端约束布置形式
4.2.3.3 钢箱与纵、横拱网格刚度匹配研究
金阜桥结构由正交异性板主桥钢箱梁体、纵、横拱及挑梁构成的网格结构和辅桥梁格构成。辅桥梁格可看作是主桥和网状格构的悬臂结构，其受力比较简单。而主桥梁体和网状格构则为全桥的主要承载和传力结构。为了使结构更加轻盈通透，增强景观视觉效果，网状格构构件做得比较纤小，纵拱和横拱截面均应利用材料自身的承载能力，挑梁也应根据受力特点采用高度变化的截面，达到纵、横拱结构与挑梁结构较佳的刚度匹配效果。因此，主桥梁体与由纵、横拱及挑梁共同组成的网状格构的刚度匹配，对于结构整体的受力显得格外重要。改变梁体的刚度对结构的景观效果影响较小，但是对改善结构的整体受力效果影响较大。图4-20 为优化前后的钢箱断面形式。分析计算结果可知，采用优化后的截面形式，结构最大应力约可降低50 MPa。
图4-20 优化前后的钢箱断面形式（左半图为优化前，右半图为优化后）
对钢箱断面形式优化前后结构的自振特性（表4-2、表4-3）进行比较分析，结果表明，由于增强主桥梁体的刚度，结构整体刚度显著增强，结构基频较优化前提高约20%，相应模态的振型质量参与系数也有所提高。结构的某些较不利的振动模态推迟或减少出现，对改善结构的动力性能也具有一定好处。
表4-2 梁体优化前结构振动特性
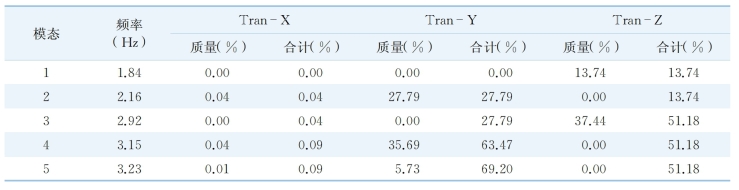
表4-3 梁体优化后结构振动特性
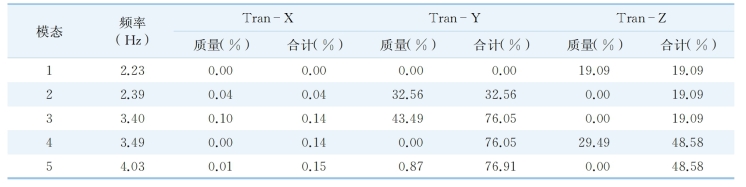
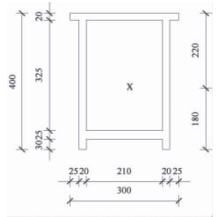
图4-21 纵拱X 优化前断面图
4.2.3.4 纵、横拱断面形式及尺寸优化
纵、横拱为宛若纤细飘带的空间扭曲曲线线形，如何在满足其纤巧截面以及优美线形要求的前提下，对其进行优化，保证结构安全可实施是结构设计的重点。以纵拱X、横拱A-5 为例，简要说明纵、横拱截面优化过程，纵拱X 优化前断面如图4 -21 所示。
恒载作用下，最不利处应力为121 MPa，对应力结果进行组成分析可知，轴向应力和主弯曲应力占比较大。不改变截面外轮廓的前提下，调整形心及几何特性，调整下翼缘板为60 mm，腹板为25 mm，调整后，恒载最大组合应力为88 MPa。
相比于纵拱，横拱断面的优化设计更为复杂，横拱A-5 优化前断面如图4 - 22 所示。
恒载作用下最不利处应力结果为104 MPa，对应力结果进行组成分析可知，应力较大的主要原因为双向弯曲应力较大。因此，在不改变截面外轮廓尺寸的前提下，调整截面形心及相关几何特性，将腹板厚度调整为16 mm、20 mm 和60 mm 三种规格。优化调整以后，恒载作用下最大组合应力为70 MPa。
综合比较纵、横拱优化前后计算结果，在降低纵、横拱应力水平的同时，桥梁其他部位的受力状况也有不同程度的改善。
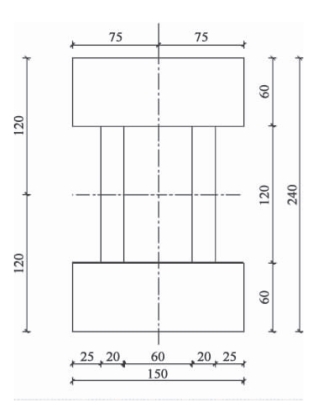
图4-22 横拱A-5 优化前断面图
有关城市桥梁设计创新与实践的文章
- 详细阅读
-
物体的受力分析及受力图制作详细阅读
受力分析时所研究的物体称为“研究对象”。这种解除了约束并被分离出来的研究对象，称为取“分离体”。将分离体所受的主动力和约束反力都用力矢量标在其相应的位置上，即得到分离体的受力图。梯子AC 部分的受力分析。在受力图上只需画出系统以外的物体给系统的作用力，这种力称为外力。......
2023-06-19
-
工艺系统的受力变形优化方案详细阅读
弹性系统在外力作用下抵抗变形的能力称为刚度。机床刚度是机床各部件抵抗变形的能力，机床刚度不足会使工艺系统变形增大，产生较大的加工误差。由于工艺系统的变形等于各组成部分变形之和，即YS=Y机床+Y刀架+Y工件+Y夹具，故工艺系统刚度的一般表达式为3.机床刚度的测定机床刚度的测定方法通常有静刚度单向测定法、三向静载测定法、生产测定法。......
2023-06-29
-
款式结构分析及改造制图方法优化详细阅读
原型制图应用临摹使学生获得了对原型结构应用的初步认知，款式结构分析与改造制图，能够为学生深入学习服装结构设计做更好的铺垫。如对原图进行款式不变、按标准号型尺寸的改造，可通过肩宽、胸、腰、臀三围的缩减，省、分割位置及袖窿深浅的控制调整等，进行款式结构改造的原型制图。......
2023-06-24
-
混凝土结构设计计算：梁的受力性能详细阅读
在长度为l0/3的纯弯区段布置仪表，以观察加载后梁的受力全过程。图3.7试验梁的构造与受力图荷载逐级施加，由零开始直至梁正截面受弯破坏。图3.8所示为钢筋混凝土试验梁的弯矩与截面曲率关系曲线实测结果。从开始加荷到受拉区混凝土开裂，梁的整个截面均参加受力，故又称为整体工作阶段。......
2023-09-19
-
剪力墙受力及错断分析详细阅读
设置翼缘是改善剪力墙平面外性能的有效措施，在不可能设置翼缘的情况下，配置钢骨是加强平面外抵抗能力的有效措施。图7-29b是另一片端部只配置钢筋的同样的剪力墙，试验时伴随着一声巨响，出现了平面外错断，表现出脆性破坏的性质。图7-30 剪力墙上出现竖向裂缝图7-31 剪力墙平面外受弯采取的措施a）加强剪力墙平面外抗弯能力 b）减小梁端弯矩......
2023-08-23
-
平谷区农业产值结构分析及优化策略详细阅读
区域农业产值结构是一个多层次、多因素的复杂系统，它具有明显的模糊性、随机性和信息不完全性，亦即灰色性。因此，农业产值结构是一个典型的灰色系统，可以通过灰色系统理论来分析山区农业经济的优势所在。图5-3 平谷区农业产值结构因素灰色关联树R11表明各业产值对大农业总产值的影响。其中以畜牧业和渔业的影响最大，其次是林果业，种植业的影响最小。R22表明林果业内部各要素产值对林果业产值的影响。......
2023-06-19
-
注塑模结构方案的痕迹分析法优化详细阅读
有些注塑模，往往是在提供有注塑样件的情形下进行设计的。这两种痕迹，特别是注塑模结构的成型痕迹，可以让我们还原注塑样件的模具结构。要素与痕迹理论对注塑模结构方案的综合分析，在对确保注塑模结构方案的完整性和正确性方面，起着极大的保障作用。注塑模结构成型的痕迹分析法和常规分析法相结合的综合分析法，才是最完美和最完善的结合，其中它们两种方法相辅相成，缺一不可。......
2023-06-30
相关推荐