线性规划与计算机程序的优化实现

1.数学模型

线性规划(Linear Programming，LP)数学模型的基本结构要素是变量、约束条件和目标函数。变量是决策者对问题需要考虑和控制的因素，故称为决策变量;约束条件是实现目标的限制因素;目标函数是决策者在问题明确之后，对问题需要达到的数学描述，它是一个极值问题。

LP问题，是求一组变量的值，在满足一组线性约束条件下，取得线性目标函数的最优解。它是水土资源综合规划中最基本的方法。

【例10.1】 某灌区灌溉规划拟采用地面水与地下水联合运用方式。地面水单位水量的效益为2万元/100万m3;地下水单位水量的效益为5万元/100万m3。由于受河道可引水量限制，引地面水不得大于400万m3，抽引地下水受可开采储量限制，不得大于300万m3。且引抽水量受渠道容量限制，地面水加2倍的地下水不得大于800万m3，试确定灌溉效益最大时的地面水和地下水的抽引量。

解:设地面水的引水量为x1(100万m3);抽取地下水的水量为x2(100万m3)。该问题的数学模型为

目标函数:

max Z=2x1+5x2

满足约束条件:

这是一个二维的LP问题。

一般来说，LP问题的数学模型可表示为:选择变量X=(x1，x2，…，xn)的值，使目标函数:

满足约束条件：

其中，目标函数中的cj(j=1，2，…，n)在资源分配问题中相当于单位产品的价格，亦称价值系数，是给定的常数。约束方程中的系数aij(i=1，2，…，m;j=1，2，…，n)及常数项bi(i=1，2，…，m)均为常数，并且cj、aij可以是任意实数，而bi必须是正数。aij表示i项资源用于j项产品每单位的用量，bi项是i项资源的总和。

上述数学模型的缩写形式为

目标函数:

满足约束条件:

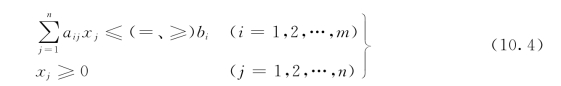
如果把LP的数学模型写成矩阵的形式，则有

求向量X=(x1，x2，…，xn)T，满足

使

这里

从数学模型知，LP问题可能有各种不同形式。目标函数有的要求实现最大化，有的要求最小化。约束条件可以是“≤”形式的不等式，也可以是“≥”形式的不等式，还可以是“=”形式。这种多样性给讨论问题带来不便。因此通常以目标函数为求最大化，且具有等号约束条件形式的LP问题，称为LP的标准形式。其数学模型表示为

目标函数:

满足约束条件:

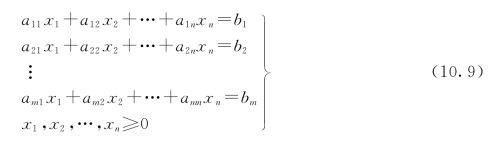
同样有其缩写形式为

目标函数:

满足约束条件:

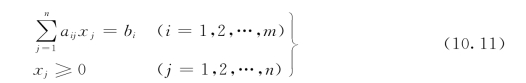
实际上，具体问题的LP数学模型，通过简单变换后，均可以化成为标准形式，并借助于标准形式的求解方法进行求解。

(1)要求目标函数实现最小化。任何一个求最小化的问题，都可以变换成为求最大化的问题。这种变换只需将目标函数式中的各项都乘以-1，即有

式(10.12)乘以-1，得

(2)约束方程组为不等式。这里有两种情况，一种是约束条件为“≤”形式的不等式，则可在“≤”号的左端加入非负的松弛变量，把原“≤”形式的不等式变为等式;另一种是约束条件为“≥”形式的不等式，则可在“≥”号的左端减去一个非负的松弛变量(也称为剩余变量)，把不等式约束变为等式约束条件。即有

若

加上松弛变量xn+i(xn+i≥0)，则

若

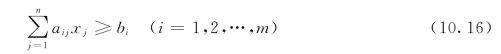
减去松弛变量xn+i(xn+i≥0)，则

显然，约束条件中增加了这些松弛变量后，式(12.15)、式(12.17)和原来的约束式(12.14)、式(12.16)是等价的。变换后的等式约束相应的目标函数应为

(3)决策变量xj不限制为非负。当变量xj并不限制为非负的情况下，则可以把该变量转换成两个非负变量之差，可以任取负值或正值，

即令xr=x′r-x″r，且使x′r≥0，x″r≥0。

2.单纯形法

(1)单纯形法的基本概念。单纯形法是求解LP问题的一个最常用方法，为了便于理解该方法的实质，仍通过[例10.1]来说明。

首先在直角坐标系中，以横轴和纵轴分别表示x1和x2的值。绘出约束条件x1≤4;x2≤3;x1+2x2≤8。由于x1和x2必须满足非负条件。在和的平面内得到凸五边形OABCD。在它所包围的区域内，及边界上的点的集合，均满足约束条件，所求问题的各种可行解必落在其中，故称这个五边形为可行区(可行域)，如图10.2所示。

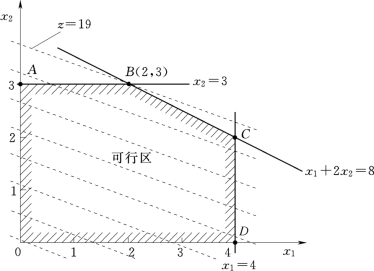
图10.2　线性规划图解法

现分析目标函数z=2x1+5x2，并把它写成

它表示以z为参数的一簇平行线，位于同一直线上的点，具有相同的目标函数值，因而称它为等值线。指在某一z值下，给定x1后，x2轴的截距，指斜率，即x1增加，相应x2的变化。当z值由小到大时，直线x2=-z沿其法线方向向右上方移动。绘出以z为参数的一组平行线，在这组平行线中，要找到一条z值最大且又位于可行区的直线，其与凸五边形OABCD有一个交点。那么这个交点必定既满足约束条件，又符合目标函数最大，这个点的坐标就是最优解。从图10.2可以找到一条z=19的直线，其通过点的坐标就是最优解，相应x1=2，x2=3，max z=19。得到问题的最优解是引取地面水为200万m3，抽地下水为300万m3，获得最大灌溉效益为19万元。

从图解法可知，LP问题的极值均出现在凸多边形的顶点，能使目标函数取极值的那个顶点就是该LP的最优解。因此，求LP问题的最优解，不必在可行区内探求，而只需要在那些顶点上寻找，这是解LP问题的出发点。

LP的理论可以证明:如果一个n个变量，m个等式约束的LP问题存在一个最优解，则在这个最优解中至少有(n-m)个变量为0，至多有m个变量不为0，然后联合求解其余m个线性方程的m个未知数，所求的解称为基本解，这样的解共有个。单纯形法就是从某一个满足非负条件的基本解(称为基本可行解)开始，转到另一个基本可行解，且使目标函数增加，经过有限次转移，最终得到满足目标函数最优的基本可行解，此即为最优解。

(2)单纯形法。前面介绍的图解法对小于三维的LP问题是可行的，当大于三维时，必须采用单纯形表法。现在仍用前面的例子，采用单纯形表法进行计算，并比较单纯形表法和图解法的计算结果。

【例10.2】 LP问题。

目标函数:

max z=2x1+5x2

满足约束条件:

引入松弛变量x3，x4，x5，上式改写为

目标函数:

max z=2x1+5x2+0x3+0x4+0x5

满足约束条件:

为了用单纯形表法进行迭代计算，将数学模型写成列向量形式，即p0=(b1，b2，…，bm)T，p1=(a11，a21，…，am1)T，…，pn=(a11，a12，…，amn)T，pn+1=(1，0，…，0)T，pn+m=(0，0，…，1)T。其步骤如下。

1)进行首次迭代，求初始基本可行解。

初始单纯形表形式:

a.将p0这一列放在左方，作为第一次取值。接下来是p1、p2和松弛变量p3、p4、p5。

b.p0左方的一列称为基底。首先将p3、p4、p5作为基底。

c.标有cj的横行，表示目标函数中各变量前的价值系数，也就是每一单位产品的价格。

d.标有ci的纵列，与cj的意义相同，仅将行变成列而已。

e.zj横行元素，由式(10.19)决定:

f.zj-cj这一横行元素，表示zj这一行的元素减去cj横行内与之相应的元素而得，(zj-cj)称为检验数，见表10.1。

作为基本初始可行解，设x1=0，x2=0，x3=4，x4=3，x5=8。显然，这个解满足约束条件，但这时变量x1、x2为0，实际上这一点无任何引抽水量，灌溉效益为零，尽管是一个“可行解”，却不是最优解，应该进行第二次迭代，现在的问题是迭代到什么地方能结束?一般可按以下准则判断。

a.如果表10.1中任何一个检验数zj-cj＜0，且在相应的纵列中所有aij≤0，则调入变量可无限增大，目标函数为无穷大。实际问题中此情况少见。

b.如果表10.1中任何一个检验数zj-cj＜0，且在相应的纵列中有几个aij＞0。这种情况说明此问题有最优解，但尚没达到最大值，应该继续迭代。

c.如果表10.1中所有检验数zj-cj≥0，这表明目标函数已经达到了最大值，迭代计算结束。

按上述准则检查表10.1中初始迭代情况，这时检验数z1-c1=-2，z2-c2=-5都为负值，这个灌溉效益为零的方案，显然是应该改善的，而且检验数相应纵列中有大于零的系数，故按准则b应该继续迭代下去。

表10.1

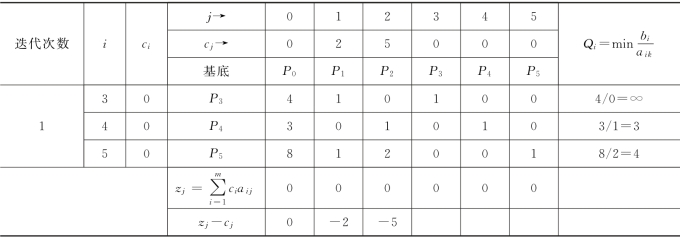
2)进行二次迭代。

作初始单纯形表，首先把松弛变量作为基底，得到初始可行解中的松弛变量虽不为0，但由于它们在目标函数中的系数均为零，相应的函数值z=0。如果我们将x1或x2放到基底中去而成为非零值，就可以使目标函数最大。所以进行第二次迭代，关键是要重新确定基底变量，且使新的基底构成后得到的基可行解，能使目标函数值增大。

a.在所有的zj-cj＜0数中，找出一个绝对值最大的数，以其所在列的pk为调入变量。在本例中z2-c2=-5，其绝对值为最大，故以p2作为调入变量pk换入基底，用虚线框出。

b.基底有调入就必须有调出，调出变量的选择可以通过计算判别数(将pk列那些大于0的系数，分别除基底变量bi所对应的系数)JUi，JUi取最小的那一行相应的变量为调出变量:

式中:JUi为相应于i个判别数;bi为相应于p0列第i个系数(即bi);aik为换入变量pk列的第i个系数。

这里选取最小值的目的是为满足变量非负条件。在本例中，

因JU4=3为最小，故选此p4作为调出向量pr，记pr(pr=p4)为调出行向量。

3)以pk作为新的基底来代替原来的pr，称为换入pk，调出pr，并做出新的计算表格见表10.2。

表10.2

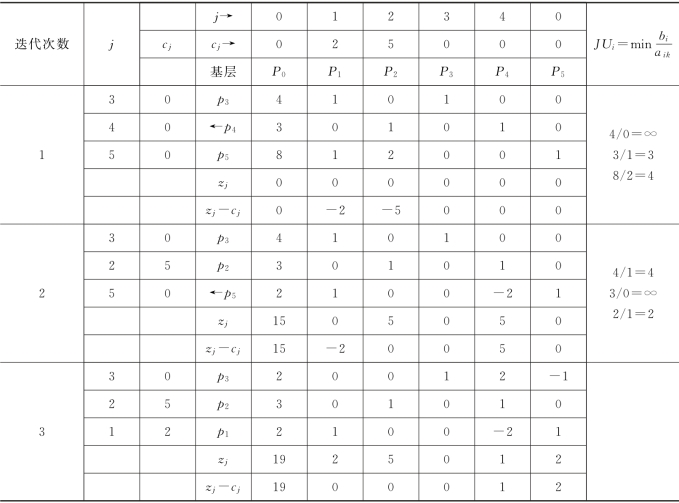
在新的表格中(第二次迭代)，位于新换出变量那一行中的元素，可由式(10.21)计算:

这就是用原表格中pr横行与pk纵列交叉处的元素ark(本例为a42=1)去除原来表格pr行的各元素就可以了。

例如:

在新的表格中，其他元素(不位于新换入向量的那一行元素)可用式(10.22)计算:

例如:

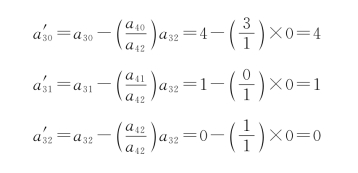
同理

又如

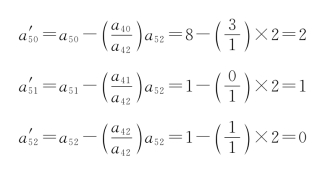
同理

这样就可以求得第二次迭代后的表格。在这表格中，目标函数z′=z0=15较初始表中z=0是好的方案。第二次迭代得到的基可行解为xj=(0，3，4，0，2)。

但检查表中还有检验数z1-c1=-2，按判别准则(2)，还应继续迭代。

4)按第二步方式继续进行迭代，直至求得最优解。

同理作出第三次迭代计算表格见表10.2，这时所有检验数(zj-cj)≥0，按判别准则c，迭代计算结束，从而求得最优解为

问题的最优解为引取地面水200万m3，抽取地下水为300万m3，所得最大灌溉效益为19万元，与图解法计算结果完全相同。

3.有关讨论

线性规划是系统工程中得到广泛应用的一种数学分析方法。由于计算机技术的飞速发展，现在已可以用它来处理成千上万个约束条件和变量的大规模LP问题。LP模型之所以被人们接受和运用，是由于LP模型本身有严格的平衡机理，它不但能反映各因素间的纵横联系，而且在求解过程中能自动完成复杂的综合平衡和调整，使优化结果一次完成。

但LP也有其本身的缺陷，因为它的最优结果是在满足既定约束条件下为实现目标而得到的，即约束条件一定，它的最优解也是一定的，因而LP模型是静止的，它只表示既定因素下的既定结果。

在编制水土资源综合治理规划时，应用LP模型，需要通过收集大量数据资料来确定模型的各种参数。但由于历史的原因，这些参数往往不能反映区域的真实情况，由此而建立的LP模型难免带有很大的局限性。因此，应将LP模型置于一个更大的动态系统之中，建立一个以LP模型为中心的模型群，将诸子模型的输出作为LP模型的输入，以充分发挥LP模型的优化功能。

通过对LP模型本身及求解过程的考查可以看出，对LP模型输入一组X、A、B、C，则有相应的Z产生，即存在下列函数关系:

Z=F(X、A、B、C)

上式称作LP的系统结构式。如果赋给不同的X、A、B、C，将有一个Z向量产生，而Z与X、A、B、C的有机结合将形成一个巨大的信息矩阵，大量的信息为优化决策提供了依据，这就是LP系统的潜力所在。因此，Z=F(X、A、B、C)是进行LP系统开发的理论基础。

LP系统结构，是一个以LP模型为中心的模型群，LP中心有4个接口与4个模型子块实行对接。

X:决策变量模块。是由决策者根据有关条件所采用的各种决策变量组合方案。决策变量向量X中的元素xj称为决策变量，它是人类实现某目标的若干行动方式。xj可由人根据不同情况和条件加以选择。

A:生产函数模块。它可以向LP中心输入不同生产技术水平矩阵A，A中的元素aij称作投入产出系数或技术系数，它表示单位j项活动对i种资源的消耗量。一般由生产的投入和科技水平所决定。

B:约束条件模块。它可向LP中心输入资源或其他限制量的不同量值。B包括BK和BL两部分，BK表示生产活动资源限制向量，一般由一组资源预测模型构成;BL表示外界需求对生产活动的限制向量，可以由一组需求模型所构成。

C:效益系数模块。它可向LP中心输入向量X的不同效益系数向量。向量C中的元素Cj表示单位活动xj所产生的实际效益。活动效益受市场、价格等因素的限制和影响，因而模块C由一组预测模型所组成。

由4个子模块输入的不同X、A、B、C，经中心LP处理后得向量Z，Z与相应的X、A、B、C不同组合，会产生不同的优化结构信息矩阵，从而为LP系统的开发提供了宝贵资源。这些优化结构信息矩阵经决策处理，可最终实现规划、预测或模拟的功能。

LP系统结构图如图10.3所示。

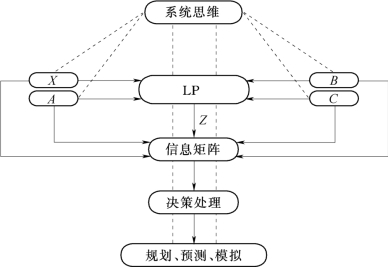
图10.3　LP系统结构图

4.单纯形法FORTRAN语言程序

单纯形法是求解LP问题的一个最常用的方法。对于复杂的LP问题，可根据单纯形表法原理，编制FORTRAN语言程序，借助电子计算机处理。

(1)程序功能。本程序可求得LP问题的有解、无解答案，以及待求变量及目标函数的最优解值。

(2)使用说明。

1)变量与参数说明:

M——原方程变量个数;

N——约束条件个数(不包括非负约束);

TYPE——目标函数类型变量，求最小值时，TYPE=-1，求最大值时，TYPE=1;

A(I，J)——约束方程组增广矩阵(I=l，2，…，N+2;J=1，2，…，N+M+1)，其中A(I，J)存储目标函数系数;A(I，M+1)由-1、0或1组成。若约束条件是“≥”时，则输入-1，若约束条件是“=”时，则输入0，若约束条件是“≤”时，则输入1，A(I，M+2)存储约束条件常数项;

Y——最优目标函数值;

X(I)——最优决策变量数组。

2)输入方法及次序:将基本资料输入abl.txt数据文件，先按序输入M，N，TYPE值，再按LP约束方程组的增广矩阵数据逐行输入，最后输目标函数各变量系数。

3)输出结果:计算结果存入ab2.txt数据文件。

INFEASIBLE　　无解，即LP问题无可行解;

UNBOUNDED　　无界，即问题无最优解;

X(I):最优解的变量值，括号内数字为变量代号。

(3)程序清单。程序清单见附录1。

(4)示例与计算结果。

【例10.3】 求xj(j=1，2)。

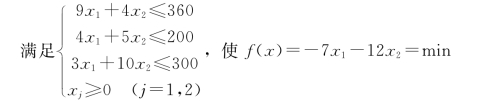
本题输入的数据为

M=2，N=3，TYPE=-1

MATRIX a

9　4　 1　360

4　5　 1　200

3　10　1　300

OBJECTIVE FUNCTION COE

-7　-12

计算机计算并打印结果:

OBJ·FUNC=-428

X(1)=20

X(2)=24

5.线性规划Matlab方法

20世纪90年代，Math Works公司推出了基于Windows平台的Matlab计算软件，它采用技术计算语言，几乎与专业领域中所使用的数学表达式相同。Matlab中的基本数据元素是矩阵，它提供了各种矩阵的运算和操作，并有较强的绘图能力，所以得到广泛应用，并成为当今应用最广、备受人们喜爱的一种软件环境。Matlab环境下的工具箱有最优化工具箱、神经网络工具箱、样条工具箱、模糊逻辑工具箱和非线性控制设计工具箱等。

下面具体介绍最优化工具箱中线性规划工具箱的使用方法。

(1)数学模型。

是向量;A和Aeq是矩阵。

(2)优化工具箱的选用。

在Matlab 6.5优化工具箱中，用于求解非线性规划的函数有linprog，常用语句包括:

x=linprog(f，A，b，Aeq，beq)

x=linprog(f，A，b，Aeq，beq，lb，ub)

x=linprog(f，A，b，Aeq，beq，lb，ub，x0)

x=linprog(f，A，b，Aeq，beq，lb，ub，x0，options)

[x，fval]=linprog(L)

[x，fval，exitflg]=linprog(L)

[x，fval，exitflg，output]=linprog(L)

[x，fval，exitflg，output，lambda]=linprog(L)

上述语句中:f为目标函数的系数矩阵;lb，ub为设置优化参数x的上、下界;fval为目标函数在最优解x点的函数值;exitflag为算法的终止标志;output为优化算法信息的一个数据结构。

(3)工程应用举例。

例题同[例10.3]。下面是求解此例的Matlab程序。

f=[-7;-12];

A=[9，4;4，5;3，10];

b=[360;200;300];

lb=zeros(2，1);

[x，fval]=linprog(f，A，b，[]，[]，lb);

输出结果为:

x=20.0000

24.0000

fval=-428.0000