在接收端，将收到的预测误差的码字解码后再与预测值相加，得到当前像素值。在视频编码中，根据预测像素选取的位置不同，预测编码可分为帧内预测和帧间预测两种。在帧内预测编码时，选取的预测像素位于要编码像素同一帧的相邻位置；而帧间预测编码时，则选取时间上相邻的像素进行预测。......
2025-09-29
灰色数列预测方法优化
【摘要】：根据数据序列建立GM(1，1)模型的步骤大致可以概括如下。这时所有模型的系数都相等，称相应的预测灰数为预测的唯一白化值。在应用时，只需要根据预测的超前长度来适当选择子序列的长度进行建模与预测。
1.基本方法与计算步骤
一般情况下，对社会、经济、水土资源的发展变化进行分析预测时，只需研究一个效果变量，即“效果”的数据序列。对于阶数，一般不超过3阶，因为阶数越大，计算越复杂且计算精度未必就高，通常为计算简单，取阶数为1，因此从预测的角度来建模，一般选定GM(1，1)模型。
即
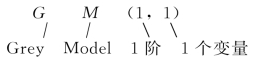
对于GM(1，1)模型，其微分方程为
求解得其时间响应函数为
若给定原始数据序列为
可分别从X(0)序列中，选取不同长度的连续数据序列，则有
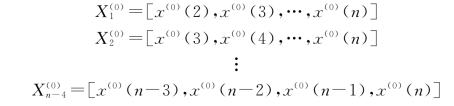
由于GM(1，1)模型，要求数据序列至少有4个数据，所以共可有(n-3)个数据序列被选取。显然，
序列是从X(0)序列中分别舍去一些数据后形成的，故称
是X(0)的子数据列。一般子数据序列必被母数据列所包含，不过可认为母序列X(0)是一个特别的子数据序列。根据数据序列建立GM(1，1)模型的步骤大致可以概括如下。
(1)确定任一子数据列(以字母序列为例):
X(0)=[x(0)(1)，x(0)(2)，…，x(0)(n)]
(2)对于数据序列作一次累加生成，记为
{X(0)}→{X(1)}
即
X(1)=[x(1)(1)，x(1)(2)，…，x(1)(n)]
其中
(3)构造矩阵B与向量Yn:
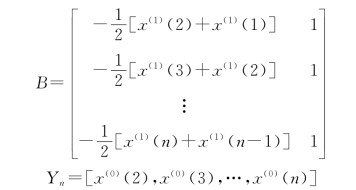
(4)用最小二乘法求解系数
(5)建立GM(1，1)模型:
(6)将
求导还原:
(7)求出
与x(0)(k)之差ε0及相对误差E0:
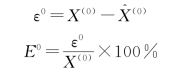
按上述步骤对每一个子序列建立GM(1，1)，都有一组系数α^:
并有相应的一组预测值，即
(k+1)，k＞1。
若记αi与ui的全体，分别为A与U，则有
A={αi|i=1，2…，n-4}
B={ui|i=1，2…，n-4}
记预测值的全体为X，则有
那么，称A为系统的发展灰数，U为系统的内生控制灰数_，X为预测灰数。若用
与
分别表示A的上界和下界(或最大与最小)，即A=
则记A的“宽度” 为m(A)，则有
我们称m(A)为发展灰数的测度，并且认为m(A)越大，则发展灰数越大。当
时，m(A)=0，则发展灰数为0。这时所有模型的系数都相等，称相应的预测灰数为预测的唯一白化值。显然，这是一种特殊的情形，不易出现。
一般来讲，当数列较长时，不必要对所有的子数据序列都建立GM(1，1)模型。在应用时，只需要根据预测的超前长度来适当选择子序列的长度进行建模与预测。大量的实践证明，进行近期或短期预测，可选用较短子数据序列(约4～10年左右);进行中长期预测，则可选择较长的子数据序列(10年以上)或母数据序列，结果较为满意。当然其关键是在于类比时间数据序列的特征与未来发展趋势是否接近。因此，在实际应用中，要定量与定性分析紧密结合，这样才能取得较好的效果。
2.灰色数列预测实例
【例9.5】 已知1998—2025年某市城镇用地情况见表9.8，试通过建立GM(1，1)模型对该市未来的城镇用地进行灰色数列预测。其具体的方法步骤如下。
表9.8 1998—2025年某市城镇用地情况 单位:万亩
解:
(1)对原始数据列x(0)作累加计算，则(https://www.chuimin.cn)
x（1）（1）=x（0）（1）=3.936
x（1）（2）=x（0）（1）+x（0）（2）=3.936+4.575=8.511
x（1）（3）=x（1）（2）+x（0）（3）=8.511+4.968=13.479
x（1）（4）=x（1）（3）+x（0）（4）=13.479+5.063=18.542
x（1）（5）=x（1）（4）+x（0）（5）=18.542+5.968=24.510
x（1）（6）=x（1）（5）+x（0）（6）=24.510+5.507=30.017
（2）构造数据矩阵B及数据向量yN：
因
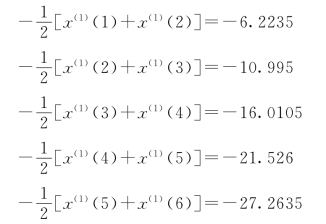
故
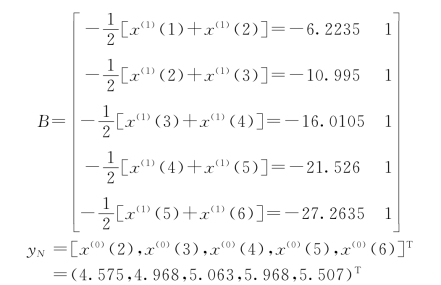
（3）计算BTB：
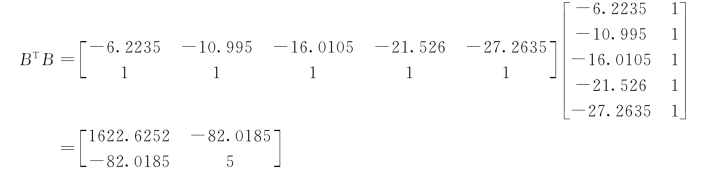
（4）求（BTB）-1：
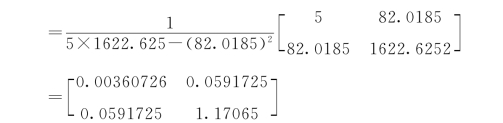
（5）计算BTyN：
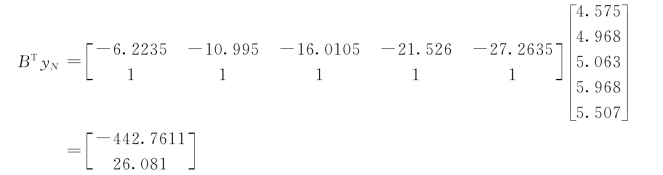
（6）计算参数列
即
α=-0.053837
u=4.332
(7)列出微分方程:
由
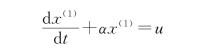
得
(8)求时间响应函数:解微分方程得时间响应函数:
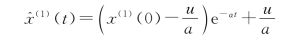
令x(1)(0)=x(0)(1)=3.936代入得
(9)求导还原:对
(1)(t+1)求导还原得
(10)回代检验计算误差:
的模型计算结果与实际值比较见表9.9。
的模型计算结果与实际值比较见表9.10。
表9.9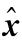 
(1)的模型计算结果与实际值比较 单位:万亩
表9.10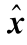 
(0)的模型计算结果与实际值比较
表9.9和表9.10中:
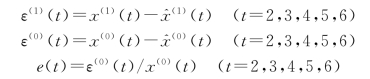
(11)预测:利用模型
进行预测，其结果见表9.11。
表9.11 某市城镇用地预测表 单位:万亩
最后需要说明的是，本章所阐述的预测方法都是最近几年常用的方法。随着科学技术的进步，计算工具的不断改善，对水土资源及其开发整治的变化将会出现新的更科学的预测方法。但是，无论哪种方法，都是认为未来也是按过去的规律发生变化，依据过去已发生的情形来预测未来将要发生的结果，并且每种方法都是根据有限的可以被“量化”处理的影响因素，通过数学手段的处理以求得未来值。由于选用的资料不同，可以选用不同的方法预测，得到的结果存在差异这也是必然的，都是不可避免的。对任何一种方法来说，都有自身固有的特点、优点、缺点和局限性，都有相对合理性与不合理性，很难得出一种方法优于另一种方法得结论。因此在进行预测时，应多选用几种方法同时进行预测，对预测的结果要认真对比分析，最后判断合理的预测值。
相关文章
- 详细阅读
-
农业用水预测方法探讨详细阅读
2.林牧渔业用水根据当地试验资料或现状典型调查，分别确定林果地和草场灌溉的净灌溉定额;根据灌溉水源及灌溉方式，分别确定灌溉水利用系数;结合林果地与草场发展面积预测指标，进行林地和草场灌溉净需水量和毛需水量预测。......
2025-09-29
-
区域电力需求的预测方法详细阅读
母线电力负荷预测一般由系统电力负荷预测来取得某一个时间的系统负荷值，并且把它分配至每一条母线上，系统电力负荷的预测是对所研究系统的未来的电力负荷需求进行预测。表6-8电力需求预测类型及其用途山西省1983—2012年的全网供电最大负荷如表6-9所示；山西省2003—2008年月度电力负荷如表6-10所示。......
2025-09-29
-
流域污染负荷预测技术优化方案详细阅读
按照0.9的排放率，南沙河流域2020年点源污水量约为20.78万m3/d。非点源污染负荷预测。考虑目前南沙河流域内监测资料较少，本次规划中的非点源污染量计算采用国家环境保护总局下发的《全国水环境容量核定技术指南》提供的输出系数法经验模型，分农业、生活和城市径流污染三方面计算非点源污染负荷，计算方法见式和式。将城市径流和农业污染累加得到一年内非点源污染输入量，南沙河干流年入河COD113.4t以及氨氮22.7t。......
2025-09-29
-
性能预测与智能维护技术优化策略详细阅读
智能维护技术是设备状态监测与诊断维护技术、计算机网络技术、信息处理技术、嵌入式计算机技术、数据库技术和人工智能技术的有机结合，其主要研究领域包括以下几个方面：远程维护系统架构和网络技术研究。多通道同步高速信号采集技术与高可靠性监测技术的研究。......
2025-09-29
-
CP机组改造后卷取精度预测优化方案详细阅读
卷取机跑偏EPC控制系统的工作目的就是要保证钢带卷齐的精度。按照现有的文献资料和设计手册中的介绍，钢带卷取时，钢带位移的偏移xi存在一个跑偏频率ωp，只有当EPC系统的频宽ωb大于ωp时，系统才能及时纠偏，这样才能保证卷齐精度。然而，该参数的范围太大，据此进行的设计不够准确，为此，又实测了机组的跑偏频率ωp和纠偏速度vp。......
2025-09-29
-
刀具磨损预测技术优化方案详细阅读
图12-4刀具磨损曲线监测信号的处理分析以及特征的提取是刀具状态监测的关键技术之一。近年来越来越多的学者利用BP神经网络来研究刀具磨损检测技术问题，利用人工神经网络预测刀具磨损是可行的也是科学的。以高速铣削过程中刀具的磨损状态为研究对象，利用刀具在不同磨损状态下的铣削力信号对不同监测技术进行研究，建立了基于BP神经网络预测......
2025-09-29
-
地铁信号设备故障预测优化方案详细阅读
当信号设备出现故障，后果往往是大面积的列车晚点，严重的故障甚至造成地铁安全性事故。目前各城市的地铁运营公司主要通过设备日常性维修来保证信号设备的稳定性，减少设备出现故障。故障预测系统模型采用BP神经网络来建立，BP神经网络在数据预测方面有其先天优势，可以无限逼近事物的未来趋势。通过实践应用验证了本地铁信号设备故障预测系统的正确性和可用性。......
2025-09-29
相关推荐