平滑预测法就是根据过去演变特征预测对象自身时间过程演变规律及未来趋势。平滑预测法包括了移动平均预测法和指数平滑法。加权指数平滑预测法需进行三次移动。一次指数平滑预测法也是一种加权预测法，加权系数为α。......
2023-07-15
指数平滑法：简单易行的预测方法
【摘要】：当时间序列数据点的分布呈非线形趋势时，常用指数平滑法确定预测模型。事实上，反复运用式，可得由式可知，第t个一次指数平滑值反映了全部前期实测数据的影响。实际应用中，常采用下式计算平滑系数:5.平滑系数α的选择指数平滑法中，α的选择对预测结果影响很大。α取值一般在0.01～0.30之间为宜。设α=0.30;=x1=201按下列公式计算，将三次的平滑值列入表9.6:求平滑系数。
当时间序列数据点的分布呈非线形趋势时，常用指数平滑法确定预测模型。其计算步骤如下。
1.求一次指数平滑值
一次指数平滑值根据本期实测数和前期的平滑值加权平均求本期平滑值。前期平滑值等于以前各期实测数的加权平滑值，能反映和代表以前的全部数据的影响，数学表达式为
式(9.17)可改写为
式中:t为数据的序号;
为第t个一次指数平滑值;xt为第t个实测值;α为平滑系数(修匀指数)，0≤α≤1。
事实上，反复运用式(9.18)，可得
由式(9.19)可知，第t个一次指数平滑值反映了全部前期实测数据的影响。
2.计算二次指数平滑值
式中:
为序列为t的二次指数平滑值;其他符号意义同前。
3.计算三次指数平滑值
式中:
为序列为t的三次指数平滑值;其他符号意义同前。
对于初始值，取
4.计算预测模型
式中:
为第T+L时段的预测值;aT、bT、cT为平滑系数;T为最后一个数据的编号;L为续T的新编序号。
实际应用中，常采用下式计算平滑系数:
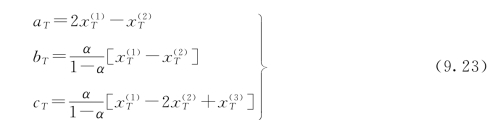
5.平滑系数α的选择
指数平滑法中，α的选择对预测结果影响很大。由平滑的基本公式可知，α越大，则近期实际数据的影响就越大;反之，近期实际数据的影响就减弱。α的选择是一个比较复杂的问题。一般而言，对于数据趋势比较稳定的序列，α取值应该小些，如果外部环境变化较快，数据系列起伏较大，则α取值应该大些，以充分反映近期数据对预测值的影响。
α取值一般在0.01～0.30之间为宜。也可对α值进行试选，求出不同的预测模型后，再用历史数据检验其精度，选择最优α值。
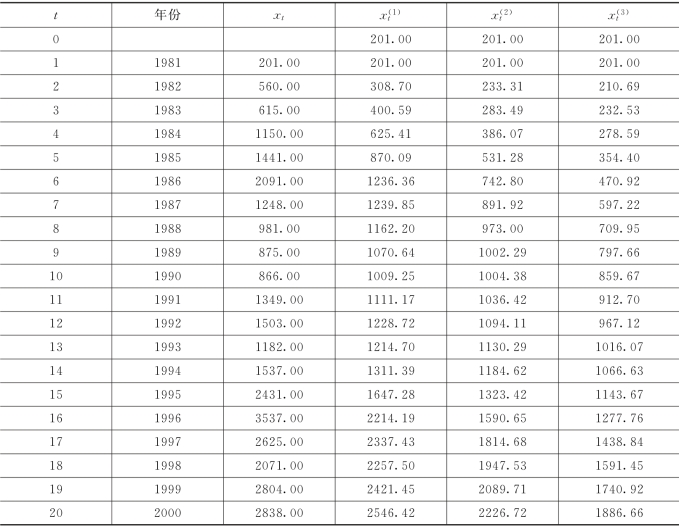
【例9.4】 某水土开发整治地区，其历年土地利用面积见表9.6，试根据历年变化规律，预测2001—2005年土地利用值。
表9.6 历年土地面积统计表 单位:亩
解:
(1)历史数据统计见表9.6。
(2)计算平滑值。设α=0.30;
=x1=201
按下列公式计算，将三次的平滑值列入表9.6:
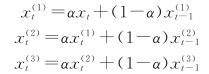
(3)求平滑系数。已知平滑值:
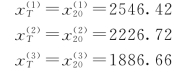
所以
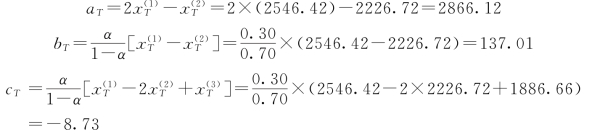
(4)求预测模型。已知aT，bT，cT的数值，求预测数学模型。
线性指数平滑值模型:
该模型说明，将以2000年2866亩为基数(aT数值，注意xT为2838亩)。今后每年按137亩速度增长。
非线性指数平滑模型:
该模型说明，今后将比线性模型按-8.73减速发展。
(5)模型应用。根据预测分析，考虑到资源潜力、劳力资源、生产力水平及市场状况，非线性指数平滑模型比较适宜。取L=1，2，3，4，5，预测2001—2005年的土地面积数量。
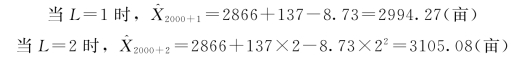
其他多年预测值见表9.7。
表9.7 2001—2005年土地利用预测值 单位:亩
有关水土资源规划与管理（第3版）的文章
- 详细阅读
-
雷兹纳稳定指数法：预测水质性能的可靠方法详细阅读
1946年雷兹纳指出，饱和指数在预测水质性能时经常出现错误的判断。因此，他提出用经验式代替饱和指数，并把的差值称作稳定指数。雷兹纳通过实验，提出了经验的稳定指数IW来进行碳酸钙垢析出的判断，定义如下：pHY可由式计算：式中 M——水中总碱度，mmol/L雷兹纳稳定指数的判断方法见表2-20。表2-20 雷兹纳稳定指数判断标准IB和IW两个指数，只能用于判断碳酸盐结垢或腐蚀的倾向性，不能提供有关计算数据，故有它的局限性。......
2023-06-30
-
情景分析预测法的优化方法详细阅读
情景分析预测法就是在长期预测时，能够辨识关键因素及其影响方法。情景分析预测法具体有未来分析法、目标展开法和间隙分析法。图6-7 情景预测法的工作步骤[案例] 用情景预测分析法预测我国GDP发展趋势1.确定主题预测国内生产总值发展趋势。因为2006年与2005年相比，增长速度为23.9%，故以此作为情景A，对此迸行运算，可得2007年国内生产总值的预测值。......
2023-07-15
-
市场调查预测法的优化方法详细阅读
企业通过市场调查分析和预测产品的需求量、销售量、市场占有率及市场潜力等。市场调查预测法包括典型调查推算法、抽样调查推算法和全面市场调查法。也有学者把市场调查预测法划分为：用户需求意见调查预测法、业务人员意见调查预测法和经理人员意见调查预测法。......
2023-07-15
-
回归模型预测法：优化方法探究详细阅读
回归模型分析预测法是根据事物内部因素变化因果关系来预测事物未来发展趋势。4）利用模型进行预测。图6-11 社会总产值预测值置信区域示意图6.3.3.2 多元线性回归预测法当预测对象Y受到多个因素X1、X2、…、Xm的影响，如果各个因素Xi与Y相关关系可以同时近似用函数关系来表示，则可以用多元线性回归预测模型进行预测。......
2023-07-15
-
移动平滑法优化方案详细阅读
移动平滑法就是对所取得的统计数据逐点推移，分段平均，以期最后得到一组具有较明显趋势的新数据。移动平滑法的预测程序框图见图9.2。图9.2移动平滑法的预测程序框图 某灌区历年人均林果产值见表9.3，试用移动平滑法建立预测模型，并求1999—2005年该灌区人均林果产值的预测值。图9.3人均林果产值的自然曲线及移动平滑预测曲线图由图9.3可知，对于直接用一次或二次移动平滑模型预测会出现滞后现象。......
2023-06-30
-
预测编码实现像素值预测的方法详细阅读
在接收端，将收到的预测误差的码字解码后再与预测值相加，得到当前像素值。在视频编码中，根据预测像素选取的位置不同，预测编码可分为帧内预测和帧间预测两种。在帧内预测编码时，选取的预测像素位于要编码像素同一帧的相邻位置；而帧间预测编码时，则选取时间上相邻的像素进行预测。......
2023-06-21
-
出版企业资金增长趋势预测法研究详细阅读
资金增长趋势预测法，就是运用回归分析法原理对过去若干期间销售收入及资金需用量的历史资料进行分析、计量后，确定反映销售收入与资金需用量之间的回归直线，并据以推算未来期间资金需用量的一种方法。采用资金增长趋势预测法，需要依据资金同销量之间的依存关系，把资金区分为不变资金、变动资金和半变动资金。也就是说，销量在一定范围内变动，这部分资金保持不变。......
2023-08-04
相关推荐