平滑预测法就是根据过去演变特征预测对象自身时间过程演变规律及未来趋势。平滑预测法包括了移动平均预测法和指数平滑法。加权指数平滑预测法需进行三次移动。一次指数平滑预测法也是一种加权预测法，加权系数为α。......
2023-07-15
移动平滑法优化方案
【摘要】：移动平滑法就是对所取得的统计数据逐点推移，分段平均，以期最后得到一组具有较明显趋势的新数据。移动平滑法的预测程序框图见图9.2。图9.2移动平滑法的预测程序框图 某灌区历年人均林果产值见表9.3，试用移动平滑法建立预测模型，并求1999—2005年该灌区人均林果产值的预测值。图9.3人均林果产值的自然曲线及移动平滑预测曲线图由图9.3可知，对于直接用一次或二次移动平滑模型预测会出现滞后现象。
移动平滑法就是对所取得的统计数据逐点推移，分段平均，以期最后得到一组具有较明显趋势的新数据。平滑即将统计数据进行平均，消除部分起伏部分，以便分析事物的发展趋势。它不是按照时间序列各期的全部数据来描述趋势，而是根据各期之前的迹象几项数据的平均值来分析时间序列的趋势。为此，在实际应用中，常需要对原始数据进行一次、二次、三次(或多次)移动平均处理，使处理后的新数列能充分反映时间序列的趋势，然后由此建立预测模型，进行预测。当原始数据的时间序列具有线性趋势时，多采用这种方法。其步骤如下。
1.计算一次移动平均值
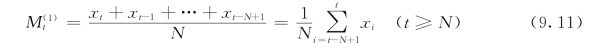
式中:
为第t期的一次移动平均值;xt为原始数列;N为移动平均值的项数，或分段数。
利用一次移动平均值作预测量，将
当作t期的预测值
然后逐步向前推移，以求出任意期的预测值。
容易看出，移动平均值是将时间序列的数据逐项移动而平均的，
仅首尾两数变化，中间各数据是依次向前推移的，因此，式(9.11)可变化为
2.计算二次移动平均值
若时间序列的各项数据经过一次移动平均后，仍不能充分反映时间序列的趋势时，可以在一次平均的基础上再求二次(或多次)移动平均值。
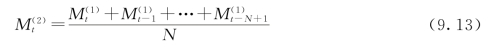
或写成:
式中:
为第t期的二次移动平均值;其他符号意义同前。
3.建立预测模型
当二次移动平均值所得的数列线性趋势明显时，可将其序列中的最后几项作为直线，求出变化趋势，建立预测模型:
其中
式中:
为第t+T期预测值;T为由t期算起的预测期数;t为目前的时期数，或为最后一个实测数据的序号。
由式(9.11)～式(9.14)可以看出，移动平均项数N值直接影响
及其预测模型。因此，N值是移动平均法预测的重要参数，必须恰当选择。较准确的作法是选择若干个N值，进行试算比较，从中选择一个既能反映预测事件的变化趋势，灵敏度又高的值。在一般情况下，当时间序列数据波动较大时，N的取值应大一些，反之的取值可小一些，一般在3～10之间。
移动平滑法的预测程序框图见图9.2。
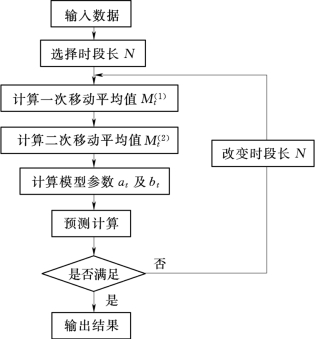
图9.2 移动平滑法的预测程序框图
【例9.3】 某灌区历年人均林果产值见表9.3，试用移动平滑法建立预测模型，并求1999—2005年该灌区人均林果产值的预测值。
表9.3 某灌区历年人均林果产值表
解:
(1)计算一次及二次移动平均值。已知t=15，取时段长N=5，根据式(9.11)计算
…，于是
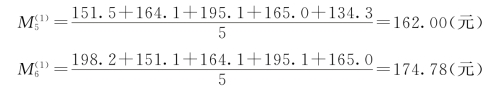
根据一次移动平均值，用式(9.13)计算
…，于是
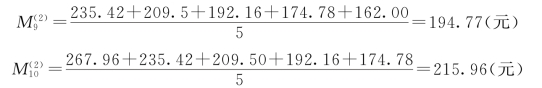
计算成果见表9.4。
表9.4 一次及二次移动平滑值计算表
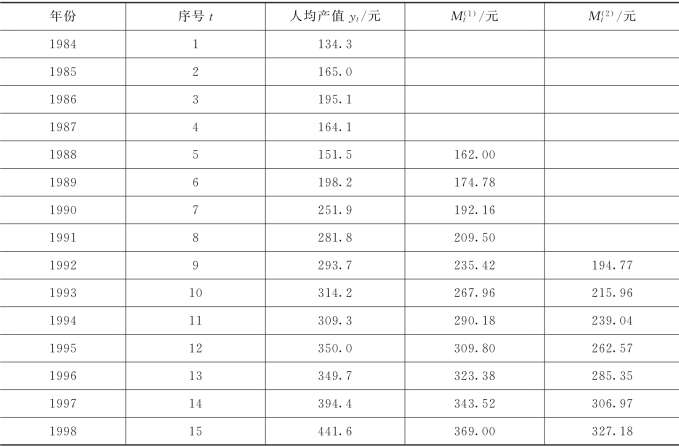
(2)建立预测模型。根据表9.4中
值计算at和bt值。
已知
t=15，N=5
由
即
由
即
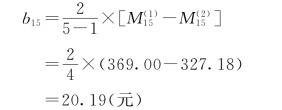
由式(9.15)得到1999—2005年该灌区人均林果产值的预测模型为
即
由预测模型计算得1999—2005年灌区人均林果产值(预测值)见表9.5。
表9.5 1999—2005年灌区人均林果产值预测表
由表9.4和表9.5绘得人均林果产值的自然曲线及移动平滑预测曲线见图9.3。
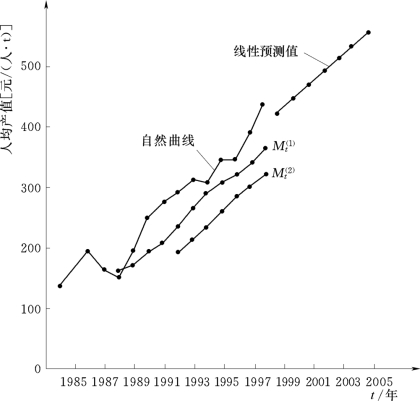
图9.3 人均林果产值的自然曲线及移动平滑预测曲线图
由图9.3可知，对于直接用一次或二次移动平滑模型预测会出现滞后现象。
有关水土资源规划与管理（第3版）的文章
- 详细阅读
-
移动卫星通信系统优化方案详细阅读
移动卫星通信系统是为舰船、车辆、飞机、边远地点用户或运动部队提供通信手段的一种卫星通信系统。为了实现全球个人通信的目标，必须借助卫星通信系统的全球覆盖特点。因此未来的全球个人通信系统将是地面陆地移动通信系统、卫星移动通信系统与地面公共通信网的结合。由于用户在移动或卫星在移动，移动卫星通信系统技术与固定业务的卫星通信系统有较大的不同。卫星移动通信系统的卫星轨道应尽量避免在此两个圆环内。......
2023-06-26
-
移动模架法施工质量保证措施优化方案详细阅读
移动模架必须进行预压试验，并进行电路、液压系统的调试和试运行，待各项试验、检测结果达到要求后，再进行整孔梁跨的浇筑施工。移动模架就位后，应严格检查桁架与桥跨中心的关系、模板中线以及高程，确保各项指标满足有关要求。根据设计要求进行预拱度设置，并跟踪、观测修正预拱度，使梁体保持良好的线形。注意保护预应力孔道，使其清洁、畅通。严格按施工工艺施加预应力，并逐步完成荷载转换，完成整跨梁体施工。......
2023-06-23
-
电子束精炼法的优化方案详细阅读
电子束精炼钛合金及其机理研究表明，高温下TiN与基体钛之间存在扩散反应，粒度为2.5mm的TiN粒子可在5min时间内完全溶解于钛中。研究证实电子束冷床炉熔炼能很好地去除各种夹杂物，获得纯净高品质的钛金铸锭。近年来，电子束熔炼又受到人们的关注。美国Honeywell International公司在电子束熔炼炉制造方面处于世界领先地位。利用该公司制造的300kW电子束熔炼炉目前能够生产出6N级的高纯钛。......
2023-06-22
-
等离子弧冷床熔炼法（PACHR）优化方案详细阅读
等离子冷床熔炼以等离子束为热源。图3-26 等离子冷床炉工作示意图电子束冷床熔炼难以控制化学成分的缺点也促进了等离子束冷床熔炼技术的发展。此外，真空等离子弧凝壳炉的熔池较浅，熔池面积较大，且无遮盖，热辐射损失大，熔池的过热度不高，只适合浇注厚壁铸件。等离子电子束熔炼又名冷阴极放电熔炼，这是一种新型的熔炼方法，近年来发展很快。等离子电弧熔炼是利用高温等离子体加热熔化金属的一种方法。......
2023-06-22
-
转子磁链观测的电流模型法优化方案详细阅读
图4.8 二相静止坐标系上的转子磁链观测模型的计算框图2.按磁场定向的二相旋转坐标系上转子磁链观测模型根据矢量控制方程式和式可以得到在二相旋转坐标系上按转子磁链定向的转子磁链观测模型，如图4.9所示。图4.9 二相旋转坐标系上按转子磁链定向的转子磁链观测模型......
2023-06-19
-
指数平滑法：简单易行的预测方法详细阅读
当时间序列数据点的分布呈非线形趋势时，常用指数平滑法确定预测模型。事实上，反复运用式，可得由式可知，第t个一次指数平滑值反映了全部前期实测数据的影响。实际应用中，常采用下式计算平滑系数:5.平滑系数α的选择指数平滑法中，α的选择对预测结果影响很大。α取值一般在0.01～0.30之间为宜。设α=0.30;=x1=201按下列公式计算，将三次的平滑值列入表9.6:求平滑系数。......
2023-06-30
-
证券投资实验实训教程：平滑异同移动平均线（M详细阅读
1）指标说明平滑异同移动平均线是近年来美国所创的技术分析工具，是以移动平均线为基础所发展出来的技术工具。根据移动平均线原理所发展出来的MACD，吸收了移动平均线的优点，克服了移动平均线假信号频繁的缺陷，对盘整行情时的股价走势判断极为有用，如图9－25所示。图9－25MACD2）运用原则DIF＞0、DEA＞0表示上涨格局。......
2023-08-12
相关推荐