齿轮传动——轮系分类与功用

活动情境

观察车床主轴箱内齿轮的分布及工作情况（见图3.80）。

图3.80　CA6140普通车床主轴传动系统图

任务要求

熟悉轮系的特点，理解轮系的工作原理，掌握传动比的计算方法。会根据输入轴的转向，判断输出轴的转向。

任务引领

通过观察与操作回答以下问题：

1.主轴箱内各齿轮是怎样工作的？传动过程中是否每个齿轮都参与啮合？

2.主轴箱是怎样进行变速的？共可输出几种转速？都是怎样实现的？

3.怎样确定传动比？

4.各啮合齿轮之间的转向有什么特点？当输入轴的转向确定之后，如何确定最后一级轴的转动方向？

5.轮系还有哪些类型？它们各有什么特点？

归纳总结

在主轴箱工作过程中，通过齿轮传动可将主动轴的较快转速变换成从动轴的较慢转速，也可将主动轴的一种转速转换成从动轴的多种转速。这种由一系列相互啮合齿轮（包括蜗杆、蜗轮）所组成的传动系统，称为轮系。如图3.81所示的桑塔纳轿车变速器，就是轮系的一种。

图3.81　桑塔纳轿车变速器

3.6.1　轮系的分类及功用

由一对齿轮所组成的传动是齿轮传动最简单的形式。但在机械设备中，只用一对齿轮进行传动往往难以满足工作要求。为了获得较大的传动，或变速和换向等，一般需要采用轮系进行传动。

1）轮系的作用

轮系有以下功能：

①大的减速或增速。

②变速、换向。

③多路输出。

④运动的合成与分解。

⑤较远距离的传动。

2）轮系的分类

轮系的形式很多，通常根据轮系在运动过程中各个齿轮的几何轴线在空间的位置是否固定，将轮系分为定轴轮系和周转轮系两大类。

（1）定轴轮系

轮系在传动中，所有齿轮轴线都是固定不动的轮系，称为定轴轮系，如图3.82所示。

（2）周转轮系

轮系在传动中，至少有一个齿轮的轴线可绕另一个齿轮的固定轴线转动的轮系，称为周转轮系（又称行星轮系）。在如图3.83所示的轮系中，齿轮2除绕自身轴线回转外，还随同构件H一起绕齿轮1的固定几何轴线回转，该轮系即为周转轮系。

在机械传动中，为满足传动的功能要求，还常将定轴轮系和周转轮系或者两个以上不共用系杆的周转轮系组成更复杂的轮系，称为混合轮系。

图3.82　定轴轮系

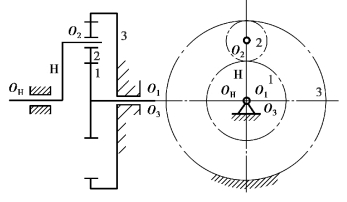
图3.83　周转轮系

3.6.2　定轴轮系传动比计算

轮系中，首末两轮的角速度（或转速）之比，称为轮系的传动比。轮系的传动比计算包括首末两轮角速度（或转速）之比的大小和两轮转向关系的确定两个方面。

1）一对圆柱齿轮的传动比

如图3.84所示，一对圆柱齿轮传动的传动比为

式中，外啮合时（见图3.84（a）），主、从动齿轮转向相反，取“-”号；内啮合时（见图3.84（b）），主、从动齿轮转向相同，取“+”号。主、从动齿轮的转动方向也可用箭头表示。

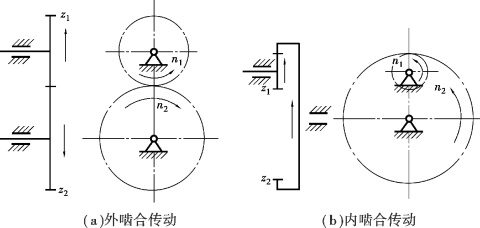
图3.84　一对圆柱齿轮的传动比

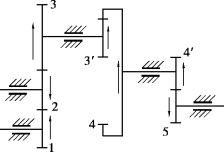
图3.85　平行轴定轴轮系的传动比

2）平行轴定轴轮系的传动比

如图3.85所示为所有齿轮轴线均相互平行的定轴轮系。设齿轮1为主动首轮，齿轮5为从动末轮，z1，z2，z3，z3′，z4，z4′，z5为各轮齿数，n1，n2，n3，n3′，n4，n4′，n5为各轮的转速。该轮系的传动比表示为

各对齿轮的传动比分别为

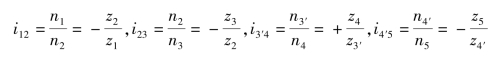
如何确定i15的大小及n5的转向呢？不难看出，将平行轴定轴轮系中各对齿轮的传动比相乘，恰为首末两轮的传动比i15，即

（负号说明n5与n1转向相反）

由上述可知：

①平行轴定轴轮系的传动比等于轮系中各对齿轮传动比连乘积，也等于轮系中所有从动轮齿数乘积与所有主动轮齿数乘积之比。设定轴轮系中轮1为主动轮（首轮），轮K为从动轮（末轮），则可得平面平行轴定轴轮系传动比的一般表达式为

式中　m——外啮合圆柱齿轮的对数。

②传动比的符号决定于外啮合齿轮的对数m。当m为奇数时，i1k为负号，说明首末两轮转向相反；当m为偶数时，i1k为正号，说明首末两轮转向相同。定轴轮系的转向关系也可用箭头在图上逐对标出（见图3.85）。

③图3.85中的齿轮2既是主动轮又是从动轮，它对传动比不起作用，但改变了传动装置的转向，这种齿轮称为惰轮。

3）非平行轴定轴轮系的传动

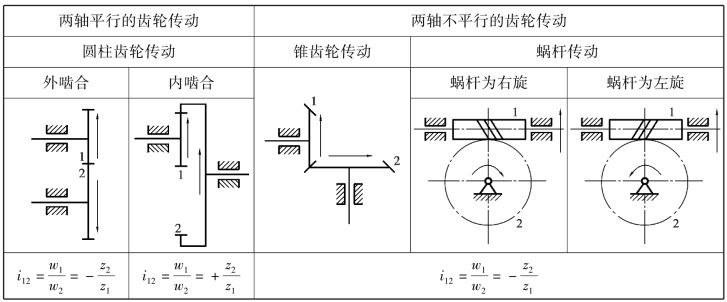
定轴轮系中，若有锥齿轮、蜗杆等传动时（见图3.86），其传动比的大小仍可用式（3.54）计算，但其转动方向只能用箭头在图上标出，而不能用（-1）m来确定。表3.24给出了常用的几种一对啮合齿轮传动时确定相对转向关系的情况。

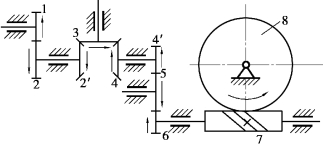
图3.86　非平行轴定轴轮系

例3.3　在如图3.86所示的定轴轮系中，已知z1=15，z2=25，z2′=z4=14，z3=24，z4′=20，z5=24，z6=40，z7=2，z8=60；若n1=800r/min，转向如图所示，求传动比i18、蜗轮8的转速和转向。

解　此轮系为非平行轴定轴轮系，其传动比大小可由式3.54计算为

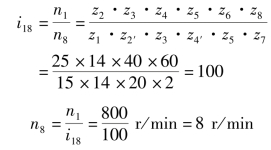
首末两轮不平行，故传动比不加符号，各轮转向用画箭头的方法确定，蜗轮8的转向最后确定，如图3.86所示。

表3.24　一对啮合齿轮传动相对转向关系确定

3.6.3　周转轮系传动比计算

1）周转轮系的组成

若轮系中，至少有一个齿轮的几何轴线不固定，而绕其他齿轮的固定几何轴线回转，则称为周转轮系。如图3.87（a）所示的轮系，即为周转轮系。其中，轮2既绕本身的轴线自转又绕O1或OH的轴线公转，称为行星轮；轮1与轮3的轴线固定不动，称为太阳轮（又称中心轮）；构件H称为系杆（又称行星架）。

2）周转轮系传动比计算

在如图3.87（a）所示周转轮系中，行星轮2既绕本身的轴线自转，又绕O1或OH公转，因此，不能直接用定轴轮系传动比计算公式求解周转轮系的传动比，而通常采用反转法来间接求解其传动比。

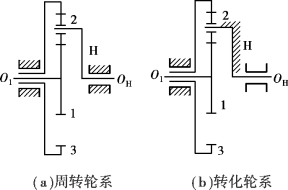
图3.87　周转轮系传动比分析

根据相对运动原理，假想给周转轮系加上一个与系杆转速nH大小相等而方向相反的公共转速-nH，则系杆H被固定，而原构件之间的相对运动关系保持不变，齿轮1，2，3则成为绕定轴转动的齿轮。这样，原来的周转轮系就变成了假想的定轴轮系，这个经过一定条件转化得到的假想定轴轮系，称为原周转轮系的转化轮系，如图3.87（b）所示。

转化机构中，各构件的转速见表3.25。

表3.25　周转轮系及其转化轮系各构件转速

既然转化轮系是假想的定轴轮系，可利用定轴轮系传动比的计算方法，列出转化轮系中任意两个齿轮的传动比。

轮1和轮3之间的传动比可表达为

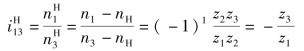
式中，表示转化轮系中轮l与轮3相对于行星架H的传动比。其中，“（-1）1”号表示在转化轮系中有一对外啮合齿轮传动，传动比为负说明：轮1与轮3在转化轮系中的转向相反。

一般情况下，若某单级周转轮系由多个齿轮构成，则传动比求法如下：

（1）求传动比大小

传动比大小为

（2）确定传动比符号

标出转化轮系中各个齿轮的转向，来确定传动比符号。当轮1与轮k的转向相同，取“+”号；反之，取“-”号。将已知转速代入公式时，注意“+”“-”号，一方向代正号，另一方向代负号。求得的转速为正，说明与正方向一致；反之，则方向相反。

例3.4　如图3.88所示的大传动比行星轮系中，已知z1=100，z2=101，z2′=100，z3=99，均为标准齿轮传动。试求iH1。

解　由式（3.55）得

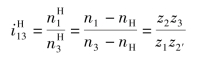
因

故有

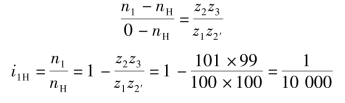
所以

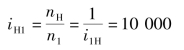
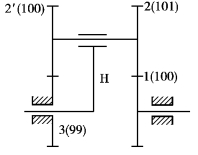
图3.88　大传动比行星轮系

图3.89　锥齿轮周转轮系

例3.5　在如图3.89所示的轮系中，已知z1=40，z2=40，z3=40，均为标准齿轮传动。试求。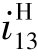

解　由式（3.55）得

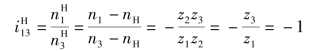
其中，“-”号表示轮1与轮3在转化机构中的转向相反。

3.6.4　轮系的功用

由上述可知，轮系广泛用于各种机械设备中，其功用如下：

1）传递相距较远的两轴间的运动和动力

当两轴间的距离较大时，用轮系传动，则减少齿轮尺寸，节约材料，且制造安装都方便，如图3.90所示。

2）可获得大的传动比

一般一对定轴齿轮的传动比不宜大于5~7。因此，当需要获得较大的传动比时，可用几个齿轮组成行星轮系来达到目的。不仅外廓尺寸小，且小齿轮不易损坏，如例3.4所述的简单周转轮系。

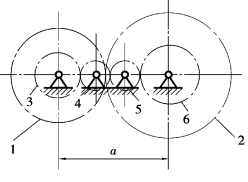
图3.90　相距较远两轴间的传动

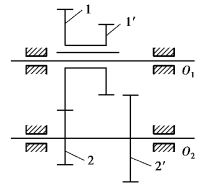
图3.91　变速传动

3）可实现变速传动

在主动轴转速不变的条件下，从动轴可获得多种转速。汽车、机床和起重设备等多种机器设备都需要变速传动。如图3.91所示为最简单的变速传动。

图3.91中，主动轴O1转速不变，移动双联齿轮1—1′，使之与从动轴上两个齿数不同的齿轮2，2′分别啮合，即可使从动轴O2获得两种不同的转速，达到变速的目的。

4）变向传动

当主动轴转向不变时，可利用轮系中的惰轮来改变从动轴的转向。如图3.83所示的轮2，通过改变外啮合的次数，达到使从动轮5变向的目的。

5）运动合成与分解

由例3.5可得

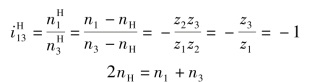
上式表明，1，3两构件的运动可合成为H构件的运动；也可在H构件输入一个运动，分解为1，3两构件的运动，这类轮系称为差速器。

如图3.92所示为船用航向指示器传动装置。它是运动合成的实例。

太阳轮1的传动由右舷发动机通过定轴轮系4—1′传过来；太阳轮3的传动由左舷发动机通过定轴轮系5—3′传过来。当两发动机转速相同，航向指针不变，船舶直线行驶。当两发动机的转速不同时，船舶航向发生变化，转速差越大，指针M偏转越大，即航向转角越大，航向变化越大。

如图3.93所示的汽车差速器是运动分解的实例。

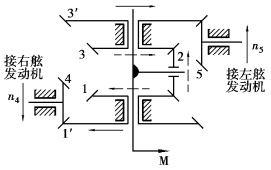
图3.92　船用航向指示器传动装置

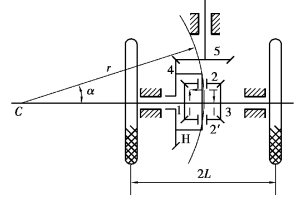
图3.93　汽车差速器

当汽车直线行驶时，左右两轮转速相同，行星轮不发生自转，齿轮1，2，3作为一个整体，随齿轮4一起转动。此时，n1=n3=n4。当汽车拐弯时，为了保证两车轮与地面作纯滚动，显然左右两车轮行走的距离应不相同，即要求左右轮的转速也不相同。此时，可通过差速器（1，2，3）轮和（1，2′，3）轮将发动机传到齿轮5的转速分配给后面的左右轮，实现运动分解。

6）其他应用

①如图3.94所示为时钟系统轮系。

②如图3.95所示为机械式运算机构。

在如图3.94所示的齿轮系中，C，B两轮的模数相等，均为标准齿轮传动。当给出适当的z1，z2，以及C，B各轮的齿数时，可实现分针转12圈，而时针转1圈的计时效果。

如图3.95所示的机构，利用差动轮系，由轮1、轮3输入两个运动，合成轮5的一个运动输出。

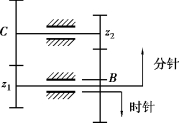
图3.94　时钟系统轮系

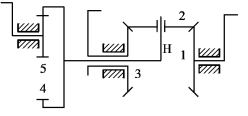
图3.95　机械式运算机构

拓展延伸

减速器简介

减速器是由封闭在刚性箱体内的齿轮传动或蜗杆传动所组成的独立传动部件。

减速器常用来降低转速，增大转矩，少数场合也用作增速装置。由于结构紧凑，传动效率高，使用寿命长，并且维护使用简单方便，因此，在机械中应用广泛。

减速器许多形式和主要参数已标准化，并由专业工厂进行生产。使用时，可根据传递的功率、转速、传动比、工作条件及总体布置要求从产品目录或有关手册中选用。必要时，也可自行设计制造。

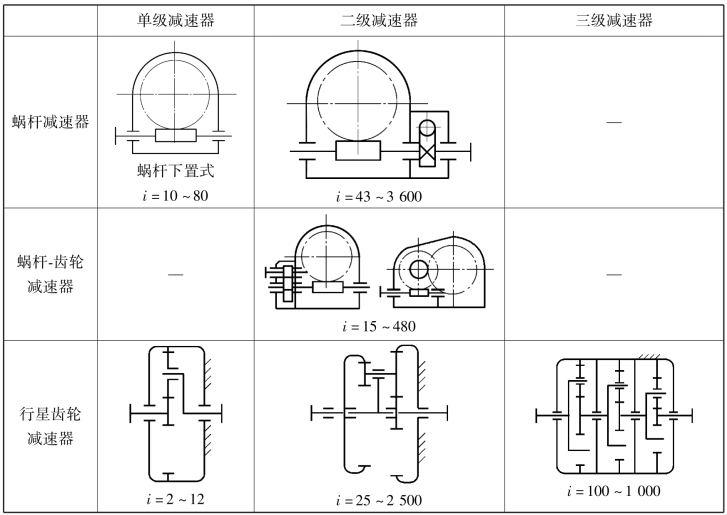
减速器按传动原理，可分为普通减速器和行星减速器两类。常用减速器的主要形式和分类见表3.26。

表3.26　常用减速器的主要形式和分类

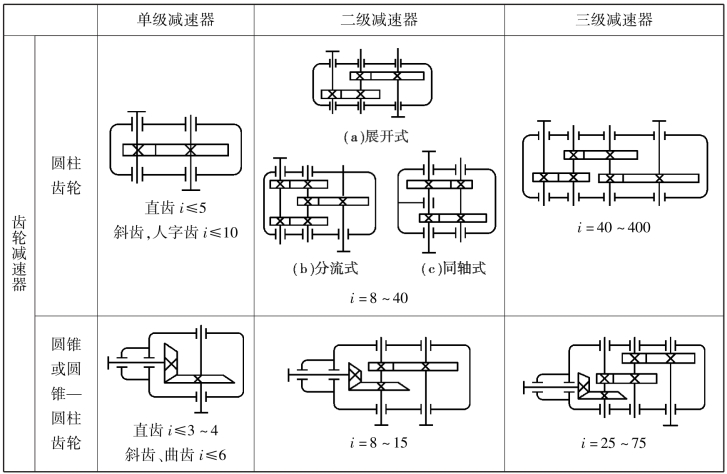
续表

自测题

一、填空题

1.由若干对齿轮组成的齿轮机构，称为________。

2.对平面定轴轮系，始末两齿轮转向关系可用传动比计算公式中________的符号来判定。

3.周转轮系由________、________和________3种基本构件组成。

4.在定轴轮系中，每一个齿轮的回转轴线都是________的。

5.惰轮对________并无影响，但却能改变从动轮的________方向。

6.如果在齿轮传动中，其中有一个齿轮和它的________绕另一个________旋转，则这轮系称为周转轮系。

7.轮系中________两轮________之比，称为轮系的传动比。

8.定轴轮系的传动比，等于组成该轮系的所有________轮齿数连乘积与所有________轮齿数连乘积之比。

9.在周转转系中，凡具有________几何轴线的齿轮，称为中心轮；凡具有________几何轴线的齿轮，称为行星轮；支持行星轮并和它一起绕固定几何轴线旋转的构件，称为________。

10.采用周转轮系可将两个独立运动________为一个运动，或将一个独立的运动________成两个独立的运动。

二、判断题

1.至少有一个齿轮和它的几何轴线绕另一个齿轮旋转的轮系，称为定轴轮系。（　）

2.定轴轮系首末两轮转速之比，等于组成该轮系的所有从动齿轮齿数连乘积与所有主动齿轮齿数连乘积之比。（　）

3.在周转轮系中，凡具有旋转几何轴线的齿轮，则称为中心轮。（　）

4.在周转轮系中，凡具有固定几何轴线的齿轮，则称为行星轮。（　）

5.轮系传动比的计算，不但要确定其数值，还要确定输入输出轴之间的运动关系，表示出它们的转向关系。（　）

6.对空间定轴轮系，其始末两齿轮转向关系可用传动比计算方式中的（-1）m的符号来判定。（　）

7.计算行星轮系的传动比时，把行星轮系转化为一假想的定轴轮系，即可用定轴轮系的方法解决行星轮系的问题。（　）

8.定轴轮系和行星轮系的主要区别，在于系杆是否转动。（　）

三、分析计算题

1.在如图3.96所示的定轴轮系中，已知各齿轮的齿数分别为z1，z2，z2′，z3，z4，z4′，z5，z5′，z6。试求传动比i16。

2.在如图3.97的轮系中，已知各齿轮的齿数z1=20，z2=40，z2′=15，z3=60，z3′=18，z4=18，z7=20，齿轮7的模数m=3mm，蜗杆头数为1（左旋），蜗轮齿数z6=40。齿轮1为主动轮，转向如图所示，转速n1=100r/min。试求齿条8的速度和移动方向。

图3.96　定轴轮系

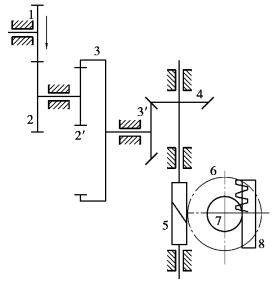
图3.97　轮系

3.在如图3.98所示的轮系中，已知各齿轮的齿数分别为z1=20，z2=18，z3=56。试求传动比i1H。

4.如图3.99所示为由圆锥齿轮组成的行星轮系。已知z1=60，z2=40，z2′=z3=20，n1=n3=120r/min。设中心轮1，3的转向相反，试求nH的大小与方向。

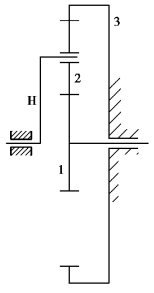
图3.98　轮系

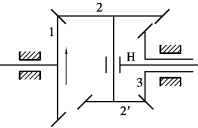
图3.99　轮系