弧焊过程信息的统计特征分析

2023-06-30 理论教育版权反馈

【摘要】：如前所述，根据焊接过程信息的属性，对带有随机性的非确定信息，需要借助于统计方法对信息的时域处理和分析，以获得均值、均方差、方差、变异系数、概率密度分布等统计信息，从而提取出具有明确物理意义的特征量。该分析仪是以焊接过程的电参数为信息源，以概率密度统计分析为主要手段，实现了对焊接过程稳定性及各统计分布的判断，进而对焊接质量做出评价。

如前所述，根据焊接过程信息的属性，对带有随机性的非确定信息，需要借助于统计方法对信息的时域处理和分析，以获得均值、均方差、方差、变异系数、概率密度分布等统计信息，从而提取出具有明确物理意义的特征量。由于统计分析方法考察的是全过程的数据信息，所以它既具有全局性，又能实现对大量数据信息的压缩处理，因此一直是对焊接过程质量、稳定性等评价的一种有效方法。然而，在将统计方法应用于带有随机现象的电弧焊接过程时必须同时满足所测信号在时序上可统计的两个条件，如图1-6所示。这一概念的物理意义表现在以下两个方面：

1）信号的整体均值U_n（t）与其某一时段U_i（t）的均值具有相同的统计意义，即某一时间段或多个时间段的信号均值与总体信号的均值在统计意义上相等，如图1-6a所示。

2）所得到的统计结果（统计值）与时间无相关性，如图1-6b所示。

只有当被测信息满足统计条件时，才能保证信息的可靠性，对信息的分析、解读就能成为科学的知识来指导并改进焊接制造各环节的质量。焊接过程的各种统计信息有均值、均方差、变异系数、事件频率以及概率密度分布等，是焊接过程信息与特征分析的数字化、可视化的一种有效认知途径。

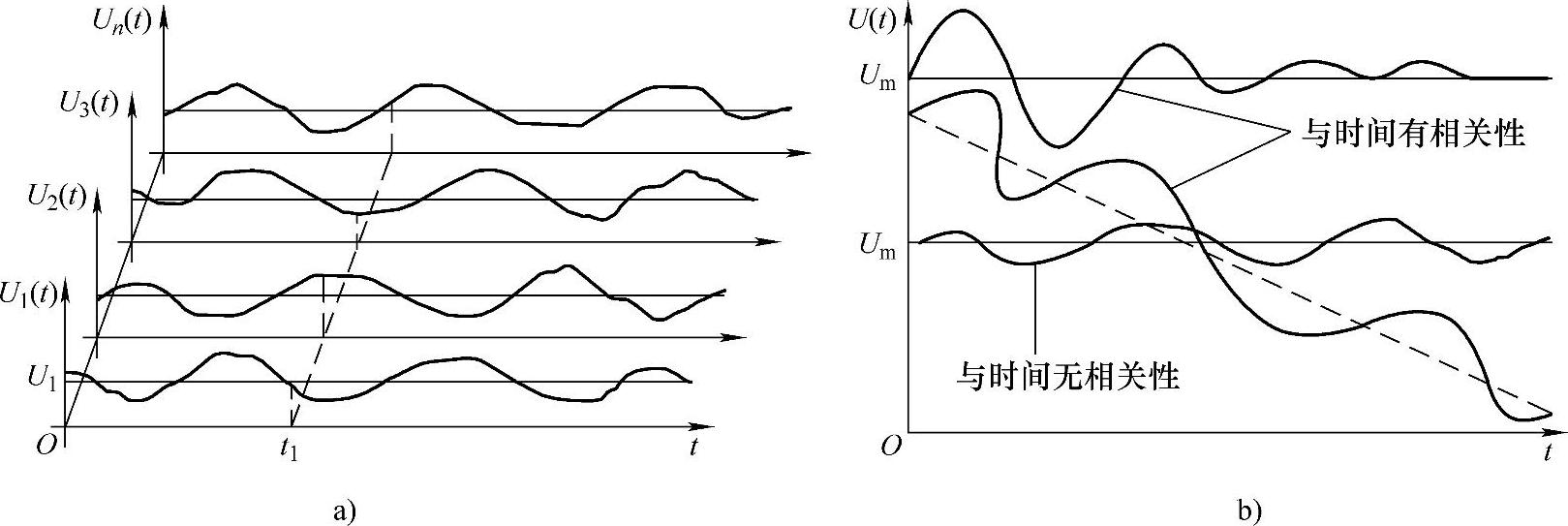
图1-6 统计量的时域稳定性示意图^[13]

a）信号的整体均值与某一时段的均值具有相同的统计意义 b）统计值与时间无相关性

对焊接过程质量进行数字化定量评估的最早开拓者之一是原德国汉诺威大学D.Rehfeldt教授^[14]。自20世纪60年代以来，他研制的“汉诺威分析仪”（Analysator Hannover）已成功地服务于包括中国在内的全世界上百个重要的焊接制造企业和研发单位。该分析仪是以焊接过程的电参数为信息源，以概率密度统计分析为主要手段，实现了对焊接过程稳定性及各统计分布的判断，进而对焊接质量做出评价。这一方法分别在材料（焊条、实心和药芯焊丝等）、设备（焊接电源）、工艺（参数优化）等三个方面都获得了较好的质量监测与分析效果，有效地帮助和指导了焊接材料品质的改进及焊接材料产品的质量监测，实现了对焊接电源缺欠和故障的诊断以及对复杂焊接工艺过程多参数的快速择优。

对连续型变量的概率密度分布的定义是^[15]：若存在非负可积函数f（x），使变量X取值于任一区间（a，b）的概率可表示为：

则称f（x）为X的概率密度函数，简称概率密度。对f（x）的进一步理解是，若x是f（x）的连续点，则：

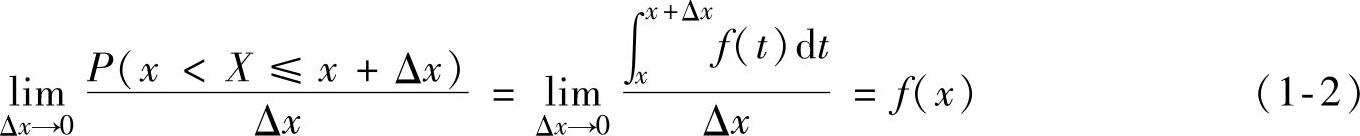
即，X的概率密度函数f（x）在x这一点的值，是X落在区间[x，x+Δx]上的概率与区间长度Δx之比的极限。在工程意义上，一事件f（x）在某一处的取值，不是事件{X=a}的概率，但是该值越大，该事件发生的概率也越大，反之亦然，从物理意义上前者表示为被观测主体的特征信息，而后者表示为某种干扰的特征信息。

图1-7是一个以焊接电压为例的概论密度分布形成原理图。图中右图为焊接时电弧电压波形图，可以看出电弧电压在每一个瞬间都在发生着变化，为了描述这一变化，在焊接电压变化的范围内，以一个合适的电压区间为组宽，把电弧电压值的范围划分为很多的组，统计每一组中采集的样本数，该组的样本数与总体样本数的比值就是一个焊接过程中某一电弧电压值（相应的组宽）出现的概率。在汉诺威分析仪中用n（%）来分别表示对应于各分组电压或电流发生的概率。

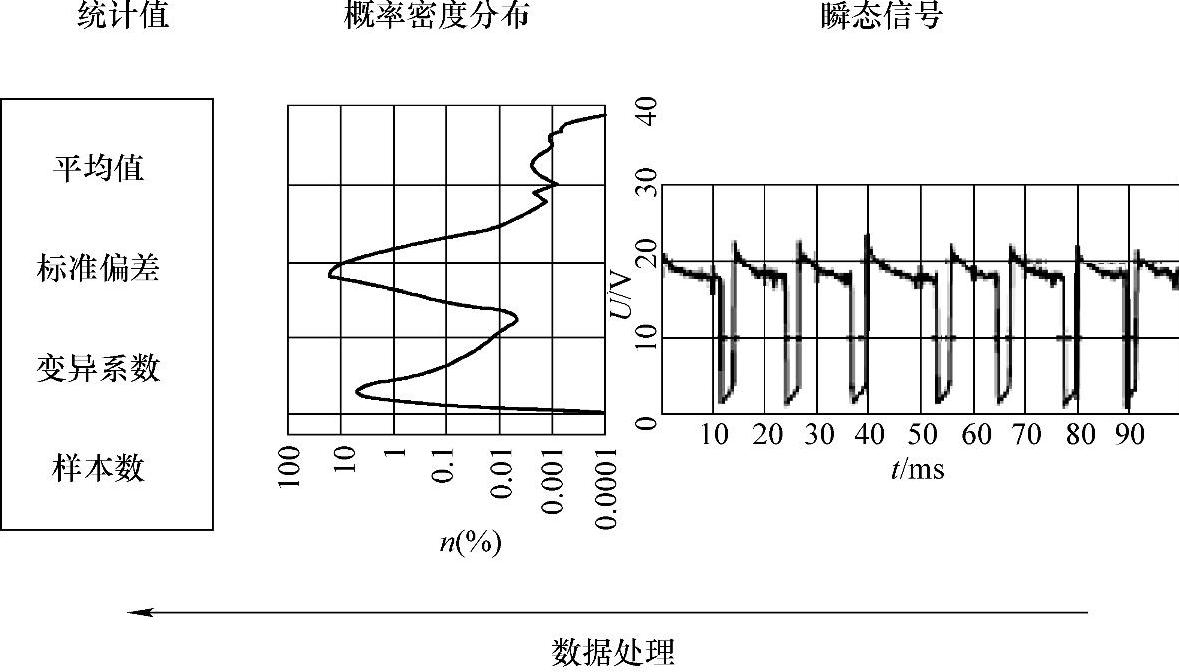
图1-7 焊接电压概率密度分布的原理图

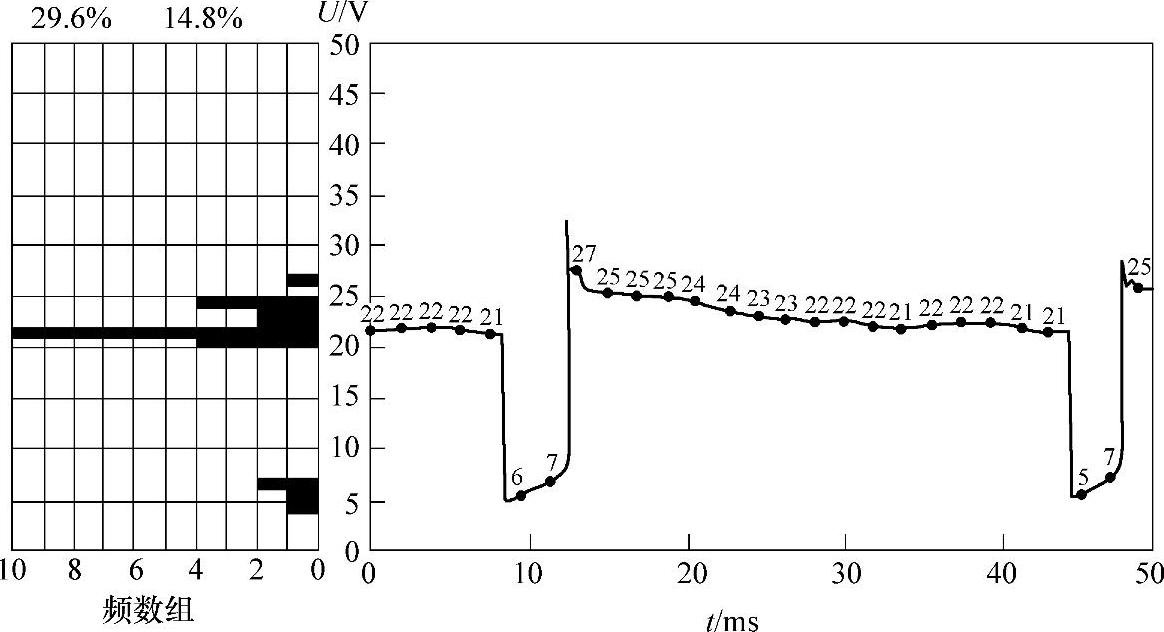
图1-8 对“频数组”统计意义的物理解释

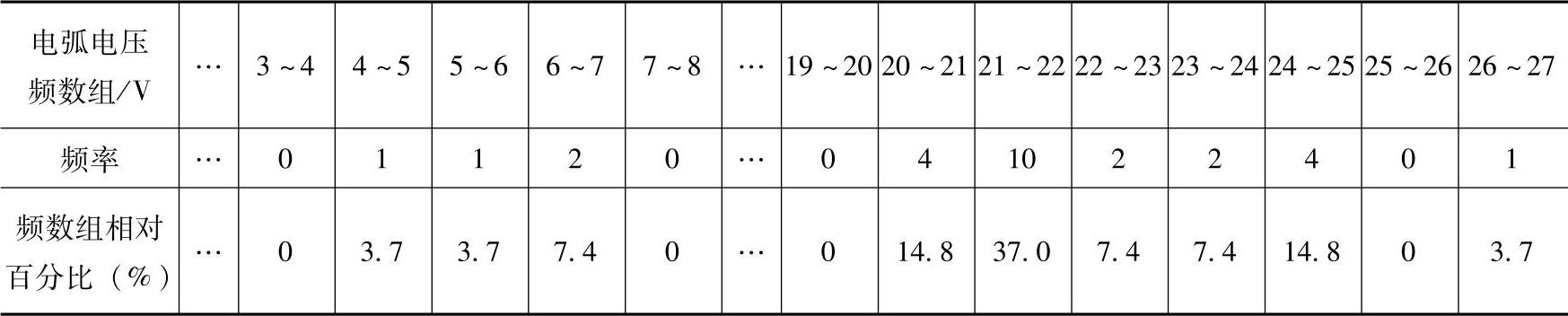
对焊接过程的大量原始数据进行统计处理时所采用的一个重要的分析方法是“频数组”及其设定的时间宽度。图1-8是对“频数组”统计意义的一个具体解释。以表1-4的数据为例，电弧电压21～22V的频数组中电压的下限和上限分别为21V和22V，组宽是1V。在焊接过程中用概率密度统计方法对电弧电压波形和各时段特征定义的示意图如图1-9所示。一个短路过渡模式是燃弧、短路（有时还有断弧或空载）等连续变化的电参数的时间序列。

由于各种因素的影响，每一熔滴经历的短路—燃弧时间并不一致，有时短路过程持续时间特别短，即熔滴只与熔池发生瞬间接触，因受焊丝末端表面张力的“牵制”而未能脱离，没有形成熔滴的过渡，或者虽从焊丝末端脱离却被排斥到熔池之外形成“飞溅”，成为一种“无效的过渡”。图1-9中T₁为短路时间（熔滴短路过渡持续的时间），T₂为燃弧时间（电弧燃烧的持续时间），T₃是加权燃弧时间（两个有效短路过渡之间的时间），T_c是周期时间（完成一个短路过渡所需的时间：T₃+T₁），U_th是电压阈值（设定的短路电压值，用于对短路频率的统计）。

表1-4 “频数组”的统计过程

对短路时间T₁、燃弧时间T₂、加权燃弧时间T₃、周期时间T_c的统计以频率分布图的形式显示，其方法是将时间横坐标按设定的时间段（组宽）进行分组，统计每个分组中采集的T₁或T₂、T3、Tc样本数，该组样本数与测试的时间相比得到该分组的频率，频率分布（Class frequency distributions）图就是以图形描述对应于各时间分组的频率分布图（即CFD图）。

在统计计算中，对焊接电参数平均值—x的定义是：

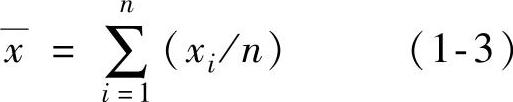
式中 x_i——第i个样本值；

n——总的样本数。

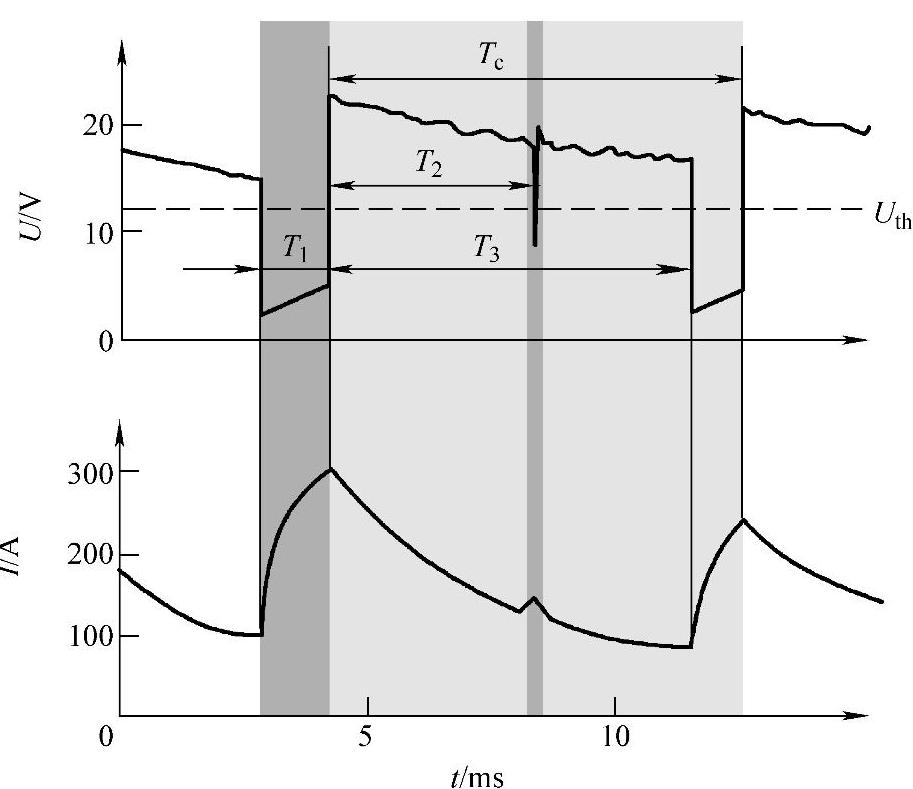
图1-9 电弧波形和各时间特征段的定义示意图

T₁—短路时间 T₂—燃弧时间 T₃—加权燃弧时间 T_c—周期时间 U_th—电压阈值

焊接过程中特征量的波动范围和程度可用标准差或变异系数表示。标准差s的定义是：

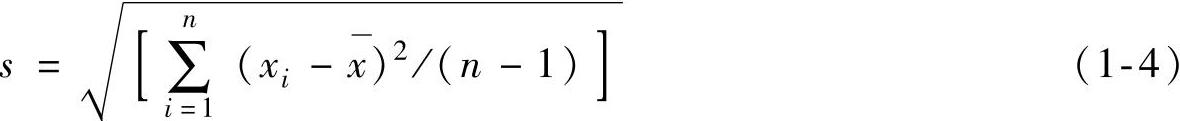
式中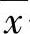——平均值；

x_i——第i个样本值；

n——总的样本数。

变异系数ν的定义是：

式中 s——标准差；

——平均值。

对焊接过程电信号进行统计分析的变量主要有：

1）电弧电压瞬时值U（t）；

2）焊接电流瞬时值I（t）；

3）短路时间T₁；

4）燃弧时间T₂；

5）加权燃弧时间T₃；

6）周期时间T_c。

对上述变量经统计分析后得到焊接过程的各特征信息，以图形表示的有：

1）电弧电压概率密度分布图U-n；

2）焊接电流概率密度分布图I-n；

3）短路时间的频率分布图T₁-N；

4）燃弧时间的频率分布图T₂-N；

5）加权燃弧时间的频率分布图T₃-N；

6）短路周期的频率分布图T_c-N；

7）时间与电压t-u关系图；

8）时间与电流t-i关系图。

以概率百分数表示的统计值有：

1）短路频率f_sc，在测试的时间内统计的短路频率；

2）短路电压概率密度n（U_s），短路电压（＜阈值电压）的概率百分数；

3）短路电流概率密度n（I_s），短路电流[I_s＞（1.5～2.0）I_m]的概率百分数；

4）平均电弧电压U_m，在测试的时间内统计的平均电弧电压；

5）平均焊接电流I_m，在测试的时间内统计的平均焊接电流；

6）平均短路时间T_1m，在测试的时间内统计的短路时间；

7）平均燃弧时间T_2m，在测试的时间内统计的燃弧时间；

8）平均加权燃弧时间T_3m，在测试的时间内，忽略瞬时短路后，统计的燃弧时间；

9）平均周期时间T_cm，在测试的时间内，统计的短路周期。

标准偏差s和变异系数ν；

1）电弧电压的标准偏差s（U）；

2）焊接电流的标准偏差s（I）；

3）电弧电压变异系数ν（U）；

4）焊接电流的变异系数ν（I）。

此外，还有各变量的最大值、最小值等。

焊接过程各统计参数与对相应信息的物理意义见表1-5。

如图1-10所示为对CO₂气体保护焊短路过渡焊接的过程分析，作为一个对上述各统计特征量及其物理意义解读的实例，对样本以电弧电压、焊接电流概率密度、短路时间T₁、燃弧时间T₂、加权燃弧时间T₃、周期时间T_c等各频率分布图的形式显示测试的结果。由图中可见：焊接电流、电弧电压概率密度分布范围表示了过程的波动与稳定程度；短路频率的分布表明了熔滴过渡尺寸的均匀性，过短的短路时间表示了过程中瞬间熔滴接触的状况，反映了熔滴的剧烈活动及其与瞬时短路飞溅率的联系；低电压的概率密度及其分布情况反映了熔滴短路过渡的行为特征。

表1-5 统计参数和焊接过程信息的解读

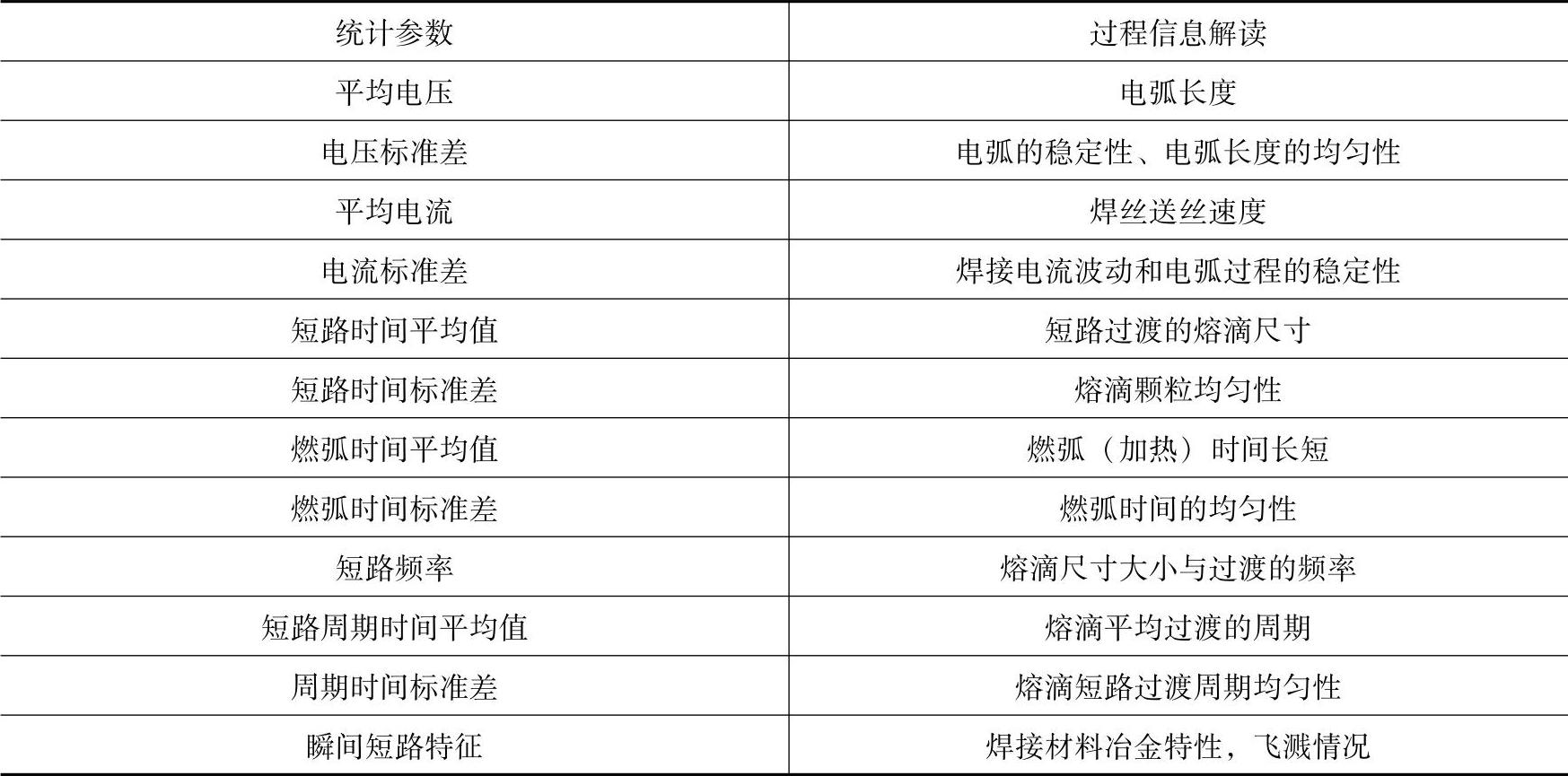
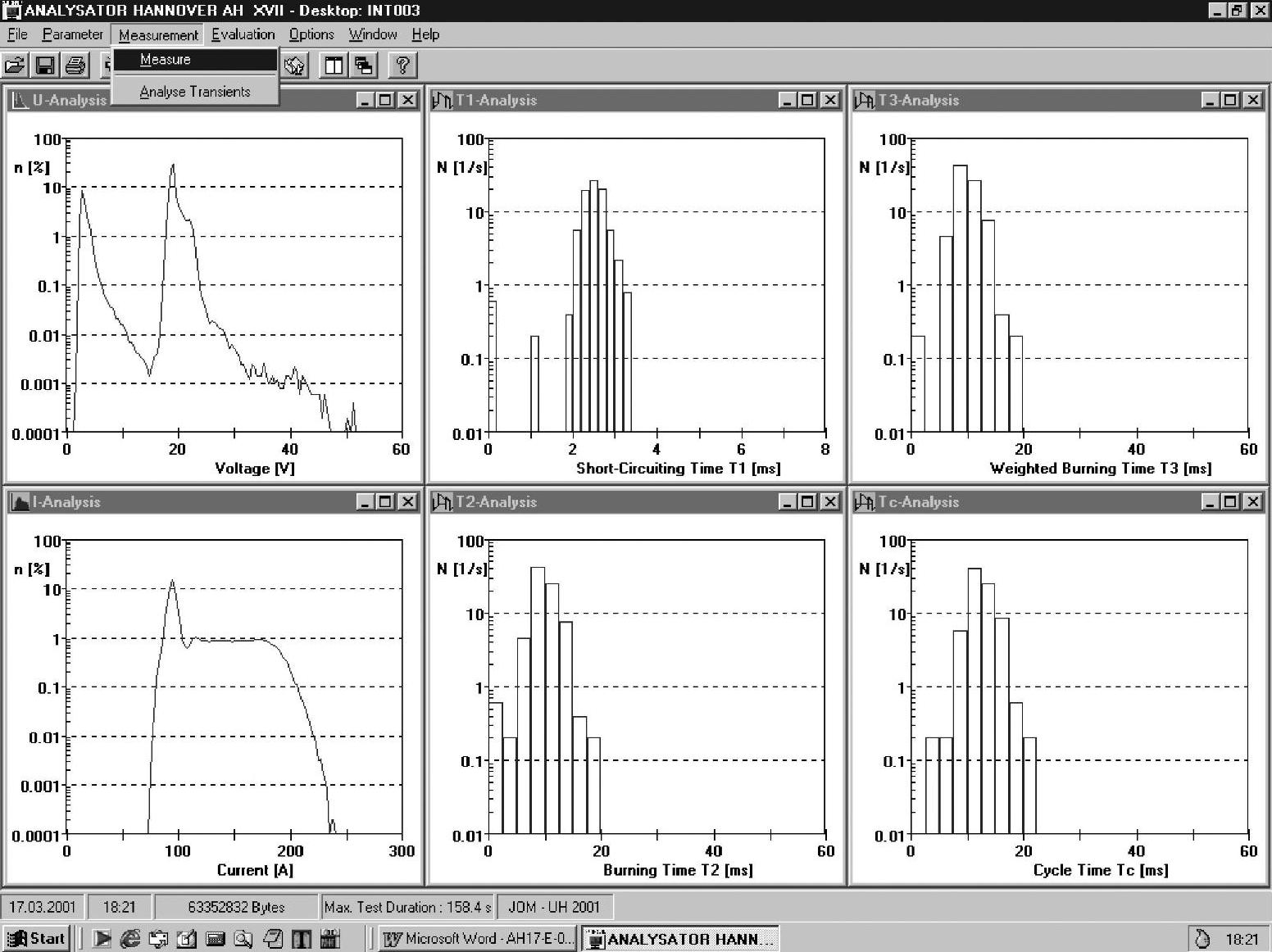
图1-10 CO₂气体保护焊短路过渡焊接过程的统计结果

弧焊过程信息的统计特征分析

相关推荐