在电磁铁结构尺寸和工作气隙值已知的情况下,直流磁路计算有以下任务。直流磁路计算可以采用分段法、漏磁系数法等方法。所分段数越多越接近于直流电磁铁的实际情况。图4-10拍合式直流电磁铁的磁动势及铁芯磁通图直流拍合式直流电磁铁示意图;线圈磁动势分态图;铁芯磁通图漏磁系数的定义及计算方法。......
2025-09-29
永久磁铁用于真空断路器、漏电保护断路器、节电型交流接触器及继电器电器中。
漏电保护断路器的漏电脱扣结构如图4-15所示。

图4-15 漏电保护断路器的漏电脱扣结构
1、8—工作气隙;2—铁轭;3—分磁板;4—空气隙;5—永久磁铁;6—铁芯;7—线圈;9—衔铁;10—拉力弹簧。
磁系统中有永久磁铁,其磁通Φ1经铁轭、工作气隙、衔铁、铁芯成为回路,磁通Φ2经铁轭、分磁板、铁芯及空气隙成为回路,磁通Φ3是线圈产生的。
图4-16和图4-17分别为VSm真空断路器永磁机构的实物图和剖视图。

图4-16 VSm真空断路器永磁机构的实物图
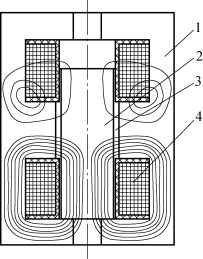
图4-17 VSm真空断路器永磁机构的剖视图
1—静铁芯;2—动铁芯;3—永磁铁;4—线圈。
永磁机构是断路器的主体,用来驱动灭弧室动触头分合动作。由2个E形铁芯作为静铁芯,永磁体处在E形铁芯的中间凸起部分,它和夹在中间的动铁芯组成特殊的双稳态对称磁路。分合闸线圈固定在2个E形铁芯之间,动铁芯从中间穿过。当动铁芯处在某一极限位置时,在这一端形成主磁回路,大部分磁通流经此端,因而在这一端和动铁芯之间产生很大的吸引力,就是触头保持力。当机构需要动作时,给线圈通过瞬态电流,产生一反向磁场,削弱主磁通,同时增大了另一端的磁通。当主磁通削弱到一定数量时,动铁芯动作,它一直运动到另一极限位置才停止,然后在这一位置形成主磁回路,产生保持力,由于其特殊的磁路结构,动铁芯只在2个极限位置机构才处于稳态,故称为双稳态对称磁路。
含永久磁铁的磁路通常简称永磁磁路,虽然永磁磁路的计算方法原则上与一般磁路相同,但也有不同之处,因为永久磁铁是利用剩磁工作的,其工作点a处于磁滞回线的第二象限部分,这部分曲线称为去磁曲线,如图4-18所示。在磁场强度为0时的磁感应强度称为剩磁感应强度(Br),在磁感应强度为0时的磁场强度称为矫顽力(Hc)。永久磁铁具有较高的矫顽力,Hc可达几百甚至几千A/m。永磁材料另一个重要性能指标是最大磁能积(BH)max,若已知材料的去磁曲线,则可求出不同磁感应强度B时的BH值,如图4-19为BH与B的关系曲线,在去磁曲线的(0,Br)点及(Hc,0)点BH值为0,而在d点其BH值最大,该最大值称为最大的磁能积,(BH)max因为永久磁铁供给工作气隙的磁能与其磁能积成正比,为使永久磁铁尺寸较小,其工作点最好在最大磁能积附近。
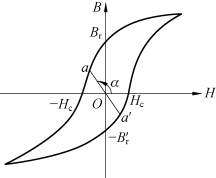
图4-18 永磁材料的磁滞回线
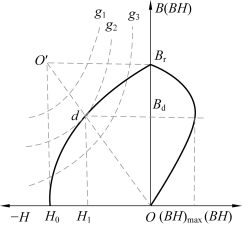
图4-19 磁能积(BH)与B的关系曲线
目前,工业生产的永磁材料主要有5类,即铸造铝镍钴系、粉末冶金铝镍钴系、铁氧体系、稀土钴系及钕铁硼系永磁材料。铝镍钴系具有较高的剩磁感应强度;铁氧体系具有较高的矫顽力;稀土钴系及钕铁硼系除具有较高的矫顽力外,还具有很高的最大磁能积,可以达到245 kJ/m3。
在永磁磁路中,永久磁铁相当于磁动势,在永磁磁路计算中也有两类任务,即已知磁路各部分尺寸和材料,求工作气隙磁通,或者已知工作气隙磁通值及磁导值,求永久磁铁的尺寸并选择永磁材料。
永久磁铁的工作状态又可分为2种情况:一是工作过程中磁路磁阻是不变的,并且永久磁铁的工作点在去磁曲线上,这种永久磁铁在装配后磁化,磁化后不进行退磁处理;二是工作过程中永磁磁路的磁阻是变化的,或者磁路中有其他变化的磁动势,或为稳定磁性能在磁化后进行退磁处理,则永久磁铁的工作点在回复线上。也就是说,在去磁曲线(见图4-20)上某个工作点m处,若加入一正磁化力(或减少磁路磁阻),使磁路中磁感应强度B增加,此时永磁材料中的B与H的关系将不沿去磁曲线上升,而是沿曲线mpr上升,当H值在负的方向增加时,B值沿曲线rqm下降,曲线mprqm称为局部磁滞曲线,由于曲线mpr与rqm很接近,可以用直线mr代替,因此将mr线称为回复线,其的斜率为tanβ,称为回复线磁导率。永久磁铁的去磁曲线如图4-20所示。
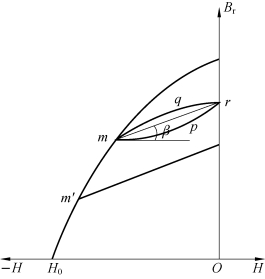
图4-20 永久磁铁的去磁曲线
去磁曲线上不同的工作点,有不同的回复线和回复线磁导率,但相差不大,材料手册中所给出的回复线磁导率(uh)是去磁曲线上(BH)max点的回复线磁导率,其值在10-6~10-5 H/m之间。下面主要介绍工作点在去磁曲线上的永磁磁路计算。
1.已知磁路各部分尺寸和材料,求工作气隙磁通Φδ值
以图4-21所示的永磁磁路为例进行分析,若衔铁不动,则磁路磁阻不变,永久磁铁工作点在去磁曲线上,按磁路的基尔霍夫第二定律,可以列出等式,即
![]()
式中:Ha——永久磁铁工作点的磁场强度(A/m);
l1——永久磁铁的长度(m);
Uδ——工作气隙磁压降(A);
Uc——铁轭及衔铁中磁压降(A)。
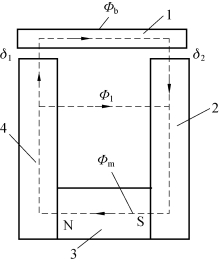
图4-21 永磁磁路
1—衔铁;2、4—铁轭;3—永久磁铁;δ1、δ2—工作气隙。
由于铁轭和衔铁中的磁通值为未知数,Uc还不能计算出来,故设

将式(4-93)、(4-94)整理,得

式中:Φδ——工作气隙磁通值(Wb);
Λδ——工作气隙磁导(H)。
设漏磁系数σ为

式中:Φm——永久磁铁内的磁通值(Wb);
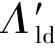 ——铁轭2和铁轭4之间的等效漏磁导(H)。
——铁轭2和铁轭4之间的等效漏磁导(H)。
而
![]()
式中:λ——铁轭2和铁轭4之间单位长度漏磁导(H);
l2——铁轭2和铁轭4通过漏磁通的长度(m)。(https://www.chuimin.cn)
由式(4-97)可知

将式(4-99)代入式(4-95)中,得
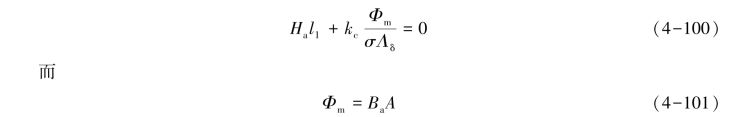
式中:Ba——永久磁铁工作点的磁感应强度(T);
A——永久磁铁的横截面积(m2)。
将式(4-101)代入式(4-100)中,可得

将式(4-102)移项,可得

由式(4-103)可知,永久磁铁工作点的![]() 值是常数,即工作点在过原点且斜率为
值是常数,即工作点在过原点且斜率为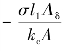 的直线上,这条直线称为负载线。
的直线上,这条直线称为负载线。
永久磁铁的工作点既在负载线上又在其材料的去磁线上,故求工作点应采用作图法,如图4-22所示,首先画出材料的去磁曲线,然后过原点作一与-H轴夹角为α的直线,α角大小可表示为

图4-22 图解法求永久磁铁的工作点

此直线即为负载线,它与去磁曲线的交点a,即为工作点,a点的横坐标为Ha,纵坐标为Ba,则Φm和Φδ值分别为

【例4-2】已知永久磁铁长度l1=20 mm,横截面积A=100 mm2。材料的去磁曲线如图4-23所示,并已知磁系统的漏磁系数σ=1.5,kc=1.2,工作气隙磁导Λδ=8×10-8 H,求工作气隙磁通。
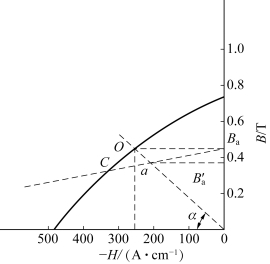
图4-23 例4-2的图
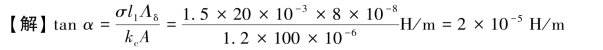
由于图4-23中横坐标每格为100 A/cm,即100×102 A/m,纵坐标每格为0.2 T,作图时应考虑其对α角的影响,故作图时
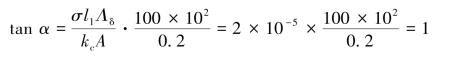
即α=45°。
过原点作一个与-H轴夹角为45°的直线,与去磁曲线交于a点,由交点a得Ba=0.48 T,Ha=240 A/cm=24×103 A/m,则永久磁铁中磁通Φm为
![]()
工作气隙磁通为
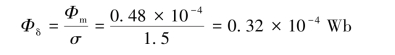
2.已知工作气隙磁通值Φδ和磁导Λδ,选择永磁材料,并确定永久磁铁的尺寸
若永久磁铁的工作点在去磁曲线上,计算永久磁铁长度l1的公式为
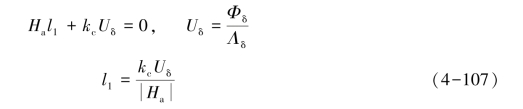
计算永久磁铁横截面积A的公式为

将式(4-107)与式(4-108)相乘,可得

由式(4-109)可知,永久磁铁的体积与![]() 的乘积成反比,要使永久磁铁体积最小,则应使永久磁铁的工作点恰好是所选材料去磁曲线上BH乘积值最大点,即(BH)max点,该点B值用Bd表示,H值用Hd表示,而Bd和Hd的计算公式为
的乘积成反比,要使永久磁铁体积最小,则应使永久磁铁的工作点恰好是所选材料去磁曲线上BH乘积值最大点,即(BH)max点,该点B值用Bd表示,H值用Hd表示,而Bd和Hd的计算公式为

当选择永磁材料时,若要求工作气隙磁通值较大,则应选用具有较大Br值和Bd值的材料。若工作气隙值较大,即工作气隙磁压降较大,应选![]() 值较大的材料,则
值较大的材料,则![]() 值也较大,使永久磁铁尺寸更为合理,永磁材料的(BH)max值当然越大越好,但还要考虑材料的加工工艺性和价格等因素。
值也较大,使永久磁铁尺寸更为合理,永磁材料的(BH)max值当然越大越好,但还要考虑材料的加工工艺性和价格等因素。
选好永磁材料之后,材料的Br、Hc和(BH)max值均可以从有关的手册中查得。先按式(4-110)和式(4-111)计算出Bd和![]() 的值,并取工作点的磁感应强度Ba=Bd,磁场强度Ha=Hd代入式(4-107)和式(4-108)中,即可得到永久磁铁长度l1和横截面积A的值。式(4-107)中的kc值及式(4-108)中σ值要采取试验的方法,即先估计一值,待初步确定磁系统尺寸后,再进行校正。
的值,并取工作点的磁感应强度Ba=Bd,磁场强度Ha=Hd代入式(4-107)和式(4-108)中,即可得到永久磁铁长度l1和横截面积A的值。式(4-107)中的kc值及式(4-108)中σ值要采取试验的方法,即先估计一值,待初步确定磁系统尺寸后,再进行校正。
【例4-3】已知永磁磁路工作气隙磁通Φδ=3.2×10-5 Wb,工作气隙磁导Λδ=8×10-8 H,求永久磁铁尺寸,并选用永磁材料。
【解】若选用铝镍钴合金,查有关手册得

设σ=1.5,kc=1.2,取Ba=Bd=0.43 T,取![]()
则永久磁铁横截面积A为
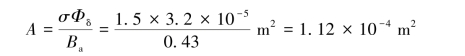
永久磁铁长度l1为
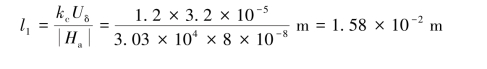
相关文章

在电磁铁结构尺寸和工作气隙值已知的情况下,直流磁路计算有以下任务。直流磁路计算可以采用分段法、漏磁系数法等方法。所分段数越多越接近于直流电磁铁的实际情况。图4-10拍合式直流电磁铁的磁动势及铁芯磁通图直流拍合式直流电磁铁示意图;线圈磁动势分态图;铁芯磁通图漏磁系数的定义及计算方法。......
2025-09-29

磁路的欧姆定律是指磁路两点间的磁压降等于通过此磁路的磁通量与其磁阻的乘积。将式(4-3)和式(4-4)代入式(4-2)中,得式中:μ——导磁体的磁导率(H/m)。图4-2导磁体磁路和空气隙磁路示意导磁体磁路;空气隙磁路2.空气隙的磁压降空气隙的磁压降为式中:Φδ——空气隙的磁通; Rδ——空气隙的磁阻(1/H)。......
2025-09-29

1.交流磁路的磁动势和磁通都是交变的交流电磁铁线圈的电压和电流是交变的,故磁动势、磁通、磁感应强度及磁场强度等均是交变的,为了简化计算,可以认为它们的波形都是正弦波,用相量表示,也可以用复数计算。......
2025-09-29

图8-14 RC滤波电路在C1=4000μF,T=0.02s条件下,电容C1的脉动系数S1为又根据RC滤波电路输出负载上的脉动系数S的计算公式(8-6)可直接求得负载RL上的脉动系数S的值。推导电路输出负载RL上的直流平均电压UO和脉动系数S的计算公式。......
2025-09-29

剪切试验试件的受力情况应模拟零件的实际工作情况进行。若以A 表示销钉横截面面积,则应力为τ 与剪切面相切,故为切应力。以上计算是以假设“切应力在剪切面上均匀分布”为基础的,实际上它只是剪切面内的一个“平均切应力”,所以也称为名义切应力。当F 达到Fb 时的切应力称剪切极限应力,记为τb。对于图5-8 所示的剪切试验,剪切极限应力为用τb 除以安全系数n,即得到许用切应力这样,剪切计算的强度条件可表示为......
2025-09-29

图13.17铅直裂隙水受力示意裂隙水在上述作用力的共同作用下沿裂隙流动或处于静止平衡状态。式就是要保证裂隙水在储油压力作用下,不向上运动。图13.18给出了倾斜裂隙水体的受力示意图。图13.18倾斜裂隙水受力示意同样,为防止油气通过倾斜裂隙逃逸进入大气,必须满足下式式中:α为裂隙倾角;其余符号意义同上。同样,考虑PcA=PcB、f=biγw,以及水力梯度i表达式,由式得因为=Lsinα,可得式中:H为水体的厚度;当取等号时,H为临界水封厚度。......
2025-09-29

断路器操作机构的疲劳问题主要是由闭合与分断过程中的动态应力应变引起,因此对断路器操作机构疲劳寿命评估的前提是分合闸过程中零部件动态应力应变的准确计算。动态应力应变的计算基于柔性体的瞬态动力学分析,瞬态动力学分析是用于确定结构在承受任意随时间变化的载荷时的动力学响应的一种方法。常用的瞬态动力学求解方法包括:完全法、缩减法、模态叠加法,本章中柔性体应力应变的计算使用模态叠加法。......
2025-09-29

一般常用检验电荷来探测、研究电场的性质。、nq,在A点所受到的电场力分别为F、2F、3F、…显然,F/q反映了电场中不同位置电场力的特性。检验电荷在电场中某一点所受电场力F与检验电荷量q的比值,称为该点的电场强度,简称场强,用公式表示为该计算值与假设值相近,说明假设的H3是正确的,表明1kg高压驱动蒸汽可以引射0.75kg的低压蒸汽;换言之,每引射1kg低压水蒸气需用1.33kg的驱动蒸汽。......
2025-09-29
相关推荐