图6.13 同步电动机空间矢量关系1.气隙磁场定向不考虑阻尼绕组的同步电动机空间矢量关系如图6.13所示。图6.13中建立了两个旋转直角坐标系,其中dq坐标系的d轴与转子励磁Ψf方向重合,mt坐标系的m轴与气隙磁链Ψδ方向重合,即按气隙磁链Ψδ方向定向。定子电流is在mt坐标系轴上投影分别为ism、ist,励磁电流在mt坐标系轴上投影分别为ifm、ift。......
2023-06-19
工程上常用的气隙磁导计算方法包括解析法、磁场分割法、图解法和经验公式法等。
图解法求解气隙磁导的实质是利用绘图的方法将磁场图景描绘出来,即将磁场分成若干具有一定尺寸比例规律的磁通路,依据磁导定义求得该子磁通路的磁导,再根据所有子磁通路的串、并联关系,确定总的气隙磁导。通常,图解法仅限于二维磁场的场景描绘。图解法虽然能够描绘出较复杂的二维磁场景,但作图过程极其复杂,工作量很大,且精度不易得到保证,因此工程上极少采用。
经验公式法是在实验或其他已被确认的磁导分析结果基础上,推导或归算出气隙磁导的计算公式或图表。显然,该气隙磁导计算方法仅适用于与经验公式相类似的特定磁场计算问题。
工程计算中最常用的磁导计算方法为解析法和磁场分割法。
1.解析法
解析法计算气隙磁导的实质是根据气隙磁导定义,采用解析方法直接求解气隙磁导,其适用范围有:磁极形状规则;气隙内磁通分布均匀;磁位等位面分布均匀;忽略磁极的边缘效应及扩散磁通等磁场问题。
1)平行磁极间气隙磁导计算
图4-5为两平行磁极间磁通分布规律,其中磁极正下方的磁通分布近似满足适用范围。除了该部分磁通外,在磁极边缘还存在扩散磁通,但在该区域内上述条件将不能得到满足。如果忽略边缘扩散磁通的影响,如当气隙长度δ与磁极几何尺寸相比较小时,工程上通常可以忽略磁极边缘的扩散磁通,并假定磁极间磁通线均匀分布,且垂直于磁极极面。此时,可以求得该气隙磁通为
![]()
式中:B——平行磁极间磁感应强度;
A——平行磁极极面积。
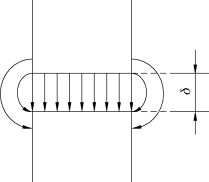
图4-5 两平行磁极间磁通分布规律
而磁极间的磁压降为
![]()
式中:H——平行磁极间磁场强度;
δ——平行磁极间气隙长度。
由气隙磁导定义,求得平行磁极间气隙磁导为

式中:μ0——真空磁导率。
工程上,平行磁极间边缘扩散磁导可以通过一定的修正系数来考虑,因此,平行磁极间气隙磁导的计算通常是利用式(4-18)计算磁极正下方的气隙磁导,再利用修正系数计算出实际的气隙磁导。
(1)边长分别为a和b的平行矩形磁极。
若![]() ,则可以忽略磁极边缘扩散磁通,气隙磁导的计算公式为
,则可以忽略磁极边缘扩散磁通,气隙磁导的计算公式为

否则,应考虑磁极边缘扩散磁通,此时气隙磁导的计算公式为
![]()
(2)直径为d的平行圆形磁极。
若![]() ,则可以忽略磁极边缘扩散磁通,气隙磁导的计算公式为
,则可以忽略磁极边缘扩散磁通,气隙磁导的计算公式为

否则,应考虑磁极边缘扩散磁通,此时气隙磁导的计算公式为
![]()
2)端面不平行磁极间气隙磁导计算
图4-6为两磁极极面夹角为θ的矩形磁极,如果磁极间气隙长度δ远小于磁极极面的最小几何尺寸,则可以忽略磁极的边缘扩散磁通,并认为磁极间磁力线是以两磁极端面中心线延长线的交点为圆心的圆弧线。由于气隙中半径为r2处的气隙长度大于半径为r1处的气隙长度,而磁极表面为等磁位,所以沿半径方向各处的磁场强度和磁感应强度不再处处相等,磁通呈不均匀分布状态。尽管如此,若沿r方向任取一元长度dr,且dr足够小,则可以认为元面积b dr内的磁通分布是均匀的,则该元面积的气隙磁导dΛδ可按式(4-18)计算,即

由此可得磁极总气隙磁导为
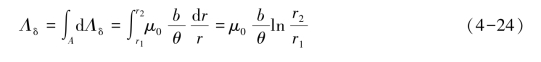
3)平行圆柱体磁极间的气隙磁导计算
图4-7(a)所示为两平行且高度相等的圆柱体磁极,其半径分别为r1和r2,中心距为y,圆柱体高度为l。直接利用气隙磁导定义计算气隙磁导较困难,因此宜采用恒定磁场与自由空间内的静电场之间场量的对偶关系来计算气隙磁导。即先求得同形状及尺寸电极间(极间介质为空气)的电容C,再根据磁场与电场场量的对偶关系求得气隙磁导Λδ。
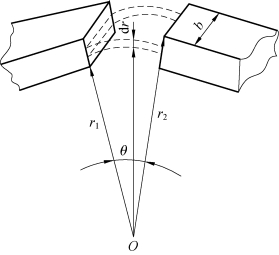
图4-6 端面不平行磁极间气隙磁导计算
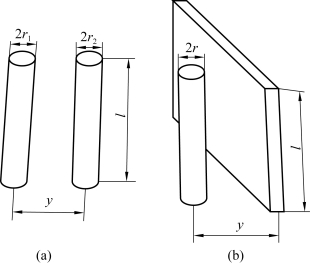
图4-7 平行圆柱体磁极间的气隙磁导计算
气隙磁导Λδ满足的关系为

式中:ε0——真空介电常数。
由式(4-25)可推得
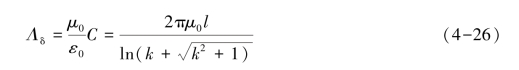
式中: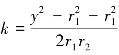 。
。
该磁极单位高度的气隙磁导为

4)平行圆柱体与平板磁极间的气隙磁导计算
图4-7(b)所示为圆柱形磁极与平板磁极构成的磁极结构,其中圆柱体磁极半径为r,平板磁极与圆柱形中心线平行,两磁极的中心距为y,高度为l,平板磁极的宽度远大于圆柱形磁极的直径。如上所述,计算该磁极结构气隙的磁导,可以先求得同形状及尺寸电极间(极间介质为空气)的电容C,再根据磁场与电场场量的对偶关系求得气隙磁导Λδ,即

磁极单位高度的气隙磁导为![]()
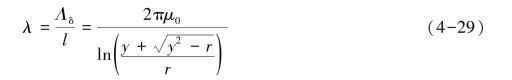
若y>4r,,则

2.磁场分割法
磁场分割法的实质是根据磁极间气隙中的磁场分布规律,找出磁通可能流经的路径,将所研究的气隙磁场区域划分为若干个有规则形状的磁通管,并按解析法求出它们的磁导,最后根据这些磁通管的并联关系,求出整个气隙的磁导。显然,磁场分割法实际上是对磁场的一种简化描述方法,如果研究区域内所划分的磁通管足够多,并且基本符合实际磁场中的磁通(磁力线)分布,则利用磁场分割法可以计算出各种形状复杂磁极间的气隙磁导,而且可以保证较高的计算精度。因此,磁场分割法更适合于磁极几何形状复杂或必须考虑边缘效应的气隙磁导计算,它是工程中经常应用的一种气隙磁导计算方法。
根据磁场分割法的气隙磁导计算的原理可知,利用磁场分割法计算气隙磁导的关键在于:
(1)合理划分磁通管,尽可能使其符合实际磁场中磁通的分布;
(2)各磁通管应具有规则的几何形状,以便于计算;
(3)利用解析法求得各磁通管的气隙磁导;
(4)根据上述所划分磁通路径的并联关系,求出整个气隙的磁导。
各磁通管的气隙磁导的计算公式为
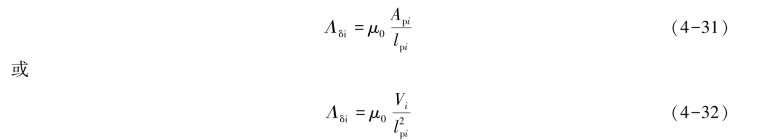
式中:lpi——第i个磁通管中磁力线的平均长度;
Api——第i个磁通管的平均截面积;
Vi——第i个磁通管的体积。
总气隙磁导等于各并联磁通管气隙磁导之和,即

图4-8为矩形截面磁极A与另一面积无限大的平板磁极B构成的磁极结构,现采用磁场分割法计算磁极间的气隙磁导,其中矩形截面磁极的边长分别为a和b,两磁极间的最小气隙长度为δ。根据磁通分布规律,可以将该气隙磁场分割为一系列具有规则形状的磁通流通路径(磁通管)。
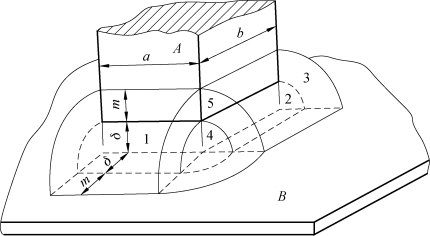
图4-8 磁场分割法划分磁通管
1)磁极A正下方的平行六面体1
平行六面体磁通管的气隙磁导为
![]()
2)磁极A端面四条棱线对磁极B的4个扩散磁通管2
每个磁通管可以简化成半径为δ的![]() 圆柱体2,该磁通管的平均气隙长度在δ和
圆柱体2,该磁通管的平均气隙长度在δ和![]() 之间,通过作图法可以确定气隙平均长度lp2=1.22δ;高度为a的磁通管体积V2a=πδ2 a/4,由此便可以求得该磁通管的气隙磁导为
之间,通过作图法可以确定气隙平均长度lp2=1.22δ;高度为a的磁通管体积V2a=πδ2 a/4,由此便可以求得该磁通管的气隙磁导为
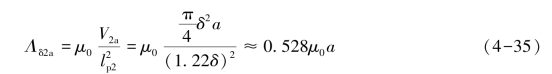
同理可求得高度为b的磁通管的气隙磁导为

3)磁极A侧面至磁极B的4个扩散磁通管3
每个磁通管可以简化为内半径为δ,厚度为m的1/4圆筒3。该磁通管的平均长度为
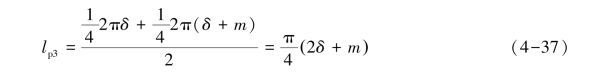
高度为a的圆筒3的体积为
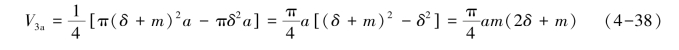
由此便可以求得该磁通管的气隙磁导为
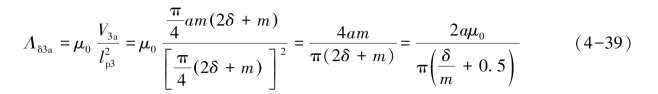
同理,高度为b的磁通管的气隙磁导为
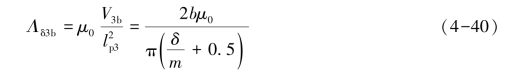
4)磁极A端面的4个棱角至磁极B的4个扩散磁通管4
每个磁通管可以简化为半径为δ的![]() 球体4。通过作图法可以确定该磁通管的平均长度为lp2=1.22δ;磁通管的体积为
球体4。通过作图法可以确定该磁通管的平均长度为lp2=1.22δ;磁通管的体积为

由此便可以求得该磁通管的气隙磁导为
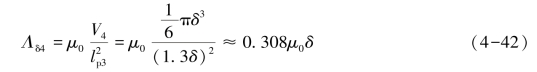
5)磁极A 4个侧面棱线至磁极B的4个扩散磁通管5
每个磁通管可以简化为内半径为δ,厚度为m的![]() 球壳5。该磁通管的平均长度为
球壳5。该磁通管的平均长度为
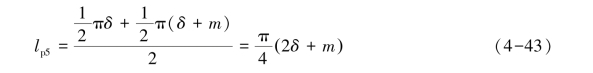
磁通管的平均截面积为
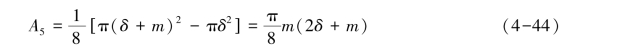
该磁通管的气隙磁导为
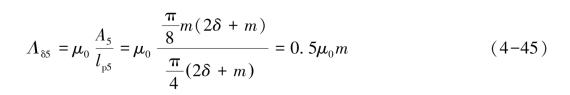
总气隙磁导为
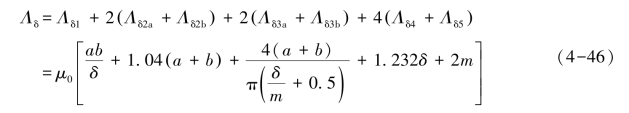
有关电器学的文章

图6.13 同步电动机空间矢量关系1.气隙磁场定向不考虑阻尼绕组的同步电动机空间矢量关系如图6.13所示。图6.13中建立了两个旋转直角坐标系,其中dq坐标系的d轴与转子励磁Ψf方向重合,mt坐标系的m轴与气隙磁链Ψδ方向重合,即按气隙磁链Ψδ方向定向。定子电流is在mt坐标系轴上投影分别为ism、ist,励磁电流在mt坐标系轴上投影分别为ifm、ift。......
2023-06-19

气隙条件是干喷湿纺工艺的重要组成部分,它是纤维聚集态结构形成的关键区域。这一过程受到多种因素的影响,包括气隙长度、吹风温度和吹风湿度、纺丝原液的温度等。由上述分析可见,Lyocell纤维生产中气隙长度设计的依据是纺丝细流在气隙中的凝固点。相反,当气隙长度确定后,必须通过工艺的调整使固化点落在气隙范围内。对于侧吹体系而言,纺丝细流的冷却效果与气隙长度、吹风温度和吹风速度相关。......
2023-06-25

自我监督的方法包括主观感觉和客观检查两个方面。但如果在运动中或运动后,除了出现上述现象外,还伴有心悸、头晕、头痛、气喘、恶心、呕吐、胸痛或其他部位的疼痛时,则表示锻炼负荷过大或健康状况不良,在进行自我监督记录时应写清具体感觉。在身体健康状况自我监督中,每周可测量1~2次体重,每次测量的时间要一致。......
2023-11-25

对于标准气用量较大或通标准气时间较长的实验工作,静态配气法不能满足要求,需要用动态配气法。动态配气法不但能提供大量的标准气,而且可通过调节原料气和稀释气的流量比获得所需浓度的标准气,这种方法尤其适用于配制低浓度的标准气。但是,这种方法所用仪器设备较静态配气法复杂,不适合配制高浓度的标准气。下面介绍几种常用的动态配气法。用渗透管法配制标准气,必须测定原料液的渗透率,其测定方法有重量法、化学分析法等。......
2023-11-23

按气隙磁场定向的可控励磁同步电动机矢量控制系统如图6.14所示。系统采用转速和电流的双闭环控制以及气隙磁链的开环控制,在基频以下保持气隙磁通不变,基频以上进行弱磁控制。图6.14 可控励磁同步电动机矢量控制系统1.转子励磁控制气隙磁通给定环节根据转速确定气隙磁通给定值Ψδ,由式计算气隙磁链电流给定值,气隙电流励磁分量Ifm=Iδ-Ism。对于定子电流的励磁分量ism,系统采用给定方式。图6.15 同步电动机矢量与相量关系......
2023-06-19

1)资源量计算体积法是一种简单快速的页岩气资源评价方法,也是勘探开发程度较低区域进行页岩气资源量评价的基本方法,也是本文采用的计算资源量方法。表6.22渝东南地区五峰—龙马溪组页岩气资源量计算表......
2023-06-24

正面上手发旋转球图3-6正面上手发旋转球动作方法。平稳抛球,直线挥臂,击球迅速,力过重心。跳发飘球抛球稳定助跑跟,双臂摆动两脚随,腰腹带动手臂甩,全掌包球落地稳。模仿练习可先进行动作分解,把完整动作分为3个部分:准备姿势、抛球与引臂、挥臂击球。......
2023-11-25

以立姿、跪姿或坐姿用双手或单手持球上举,直臂或屈臂做向前、向后抛掷实心球练习。图6-28抛球图6-29挥臂图6-30辅助扣球图6-31投掷徒手用扣球手法挥臂抽击高点的树叶。杠铃连续向斜上方快速推举练习。④在攀登架上做举腿绕环练习。⑤一人在凳上做仰卧绕“8”字回环,另一人固定其脚。图6-39负重转体图6-40负重体绕环力量练习......
2023-11-25
相关推荐