磁路的基尔霍夫第二定律解析

2025-09-29 理论教育版权反馈

【摘要】：磁路的基尔霍夫第二定律是指沿磁路的任一闭合回路，磁压降的代数和等于与该回路磁通相交链的线圈磁动势的代数和，即式是由全电流定律推导出来的。在有空气隙的磁路中，磁路的基尔霍夫第二定律也可以表示为由上述可知，磁路计算的基本定律与电路计算有相似之处，而且正如电路计算中的欧姆定律和基尔霍夫定律，不仅适用于直流电路，同时也适用于交流电路，交流磁路计算也和交流电路一样，要用复数计算。

磁路的基尔霍夫第二定律是指沿磁路的任一闭合回路，磁压降的代数和等于与该回路磁通相交链的线圈磁动势的代数和，即

式（4-11）是由全电流定律推导出来的。如果磁通的方向与环绕方向一致，则该段的磁压降为正，反之为负。当磁动势正方向（磁动势正方向和电流正方向应符合右手螺旋定则）和环绕方向一致时，该磁动势为正，反之为负。

在有空气隙的磁路中，磁路的基尔霍夫第二定律也可以表示为

pagenumber_ebook=104,pagenumber_book=98

由上述可知，磁路计算的基本定律与电路计算有相似之处，而且正如电路计算中的欧姆定律和基尔霍夫定律，不仅适用于直流电路，同时也适用于交流电路，交流磁路计算也和交流电路一样，要用复数计算。(https://www.chuimin.cn)

由于磁路计算与电路计算有相似之处，所以在分析和计算磁路时，常依照电路的形式，将磁路表示成类似电路的等效磁路图，用电动势的符号代表磁动势，用电阻的符号代表磁阻，画出等效磁路图。图4-4为拍合式直流电磁铁在忽略漏磁通时的等效磁路，由于忽略了漏磁通，铁芯和铁轭中的磁通值是一定的，所以其磁阻可以各用一个集中磁阻表示，本来是分布在铁芯长度上的磁动势，可以用一个集中磁动势来表示。

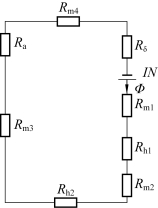
pagenumber_ebook=104,pagenumber_book=98

图4-4　拍合式直流电磁铁的等效磁路

IN—磁动势；Rδ—工作气隙磁阻；Ra—楞角气隙磁阻；Rh1、Rh2—非工作气隙磁阻；Rm1—极靴磁阻；Rm2—铁芯磁阻；Rm3—铁轭磁阻；Rm4—衔铁磁阻。

磁路计算比电路计算困难得多，因为导磁体是用铁磁材料制成的，它的磁导率不是常数，而是随磁感应强度的大小在相当大的范围内变化，所以导磁体的磁阻不是常数，而是非线性的；空气的磁导率虽然是常数，但是，由于气隙磁通分布的不均匀性，气隙磁导的计算也不容易得到精确的结果。磁路中除了主磁通还有漏磁通，使铁芯和铁轭长度上各点的磁通值均不相同，而且磁动势也是不均匀分布的。因此，磁路计算比电路计算复杂。

磁路的基尔霍夫第二定律解析

相关推荐