众所周知，如果电力变压器中性线断路，而三相负载又不平衡时，很容易造成电器设备因过电压而损坏。图3-68交流电源中性线断路报警器工作原理：正常时，A点电位即为地电位，发光二极管VH不发光。当三相负载不对称时，A点就产生电位，负载不对称程度越严重，A点电位也越高。A点对地电压经二极管VD半波整流，加在限流电阻R1和分压电阻R2上，发光二极管VH得到足够的电压而发光，发出报警信号。图3-69利用光电耦合器的报警或保护电路......
2025-09-29
在三相交流中的电动力优化方案
【摘要】：如图2-10所示，作用在A相导体上的电动力是变化的。图2-11作用在B相导体上的电动力由式和式可知，B相导体受到的最大电动力是A相导体的最大电动力的倍。无论是B相导体还是A、C相导体所受到的电动力都是交变的，其交变频率为电源频率的2倍，电动力的大小及方向均随时间变化。图2-13三相导体作等边三角形布置式表明，A相导体受到的电动力其大小和方向随时间而变，可用表示，的端点随时间沿圆周移动。
设有三相导线A、B、C在同一平面内直列布置，导体间的距离为a，如图2-9所示。
三相导体中分别流过的三相正弦对称稳态电流力为
图2-9 三相导体为直列布置
下面分析各相导体所受的电动力。
1.作用在A相导体上的电动力
根据图2-9所规定iA、iB、iC的方向，如果某瞬间iA与iB（iC）流过导体的方向相同，则A相导体与B相（C相）导体产生吸力。现规定A相导体与B相（C相）导体之间的吸力方向为正方向，则作用在A相导体上的电动力，可以认为是B相和C相导体单独作用的叠加，即FA=FAB+FAC，此时FAB、FAC为正值。则由电动力公式（2-83）得
式中：
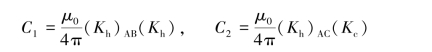
其中（Kh）AB和（Kh）AC分别为A、B相和A、C相导体间的回路因数，Kc为截面因数。
由于导体截面相同，只是A、C相的距离为A、B相距离的2倍，故
。由此可得
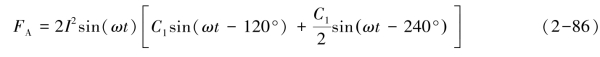
变换可得
要求最大电动力，所以令FA的导数为0可以找出最大电动力时的ωt值。
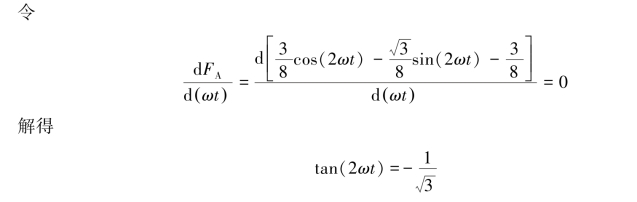
则ωt=nπ+75°（n=0，1，2，…）或ωt=nπ+165°（n=0，1，2，…），将ωt=nπ+75°
代入FA中，则
表示A相导体受最大电动斥力为0.808F0，F0=CI2。
将ωt=nπ+165°代入FA中，则
表示A相导体受最大电动吸力为0.058F0。
如图2-10所示，作用在A相导体上的电动力是变化的。当ωt=nπ+75°时，导体受最大电动斥力为0.808F0；当ωt=nπ+165°时，导体受最大电动吸力为0.058F0，斥力的最大值远大于吸力最大值。
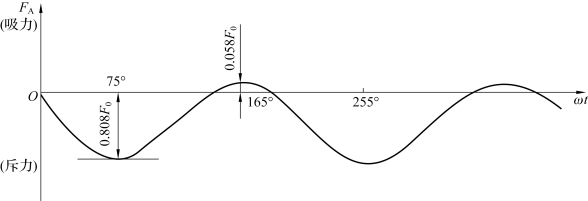
图2-10 作用在A相导体上的电动力
2.作用在B相导体上的电动力
作用在B相导体上的电动力，可以认为是A相和C相导体单独作用的叠加。现假定B相导体受A相导体作用电动吸力的方向为FB正方向，则(https://www.chuimin.cn)
式中：
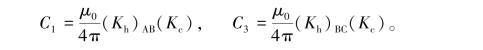
由于A相和C相导体截面相等，且A、B相与B、C相距离相等，故C1=C3，则
求B相所受的最大电动力的过程如下。
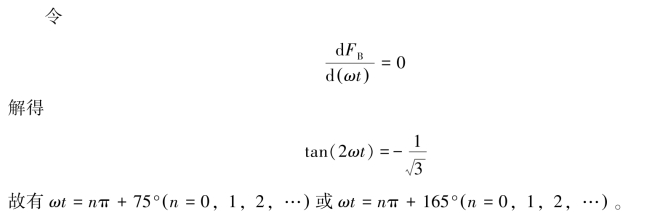
将ωt=nπ+75°代入式（2-91）中，得
将ωt=nπ+165°代入式（2-91），得
由式（2-92）和式（2-93）可知，B相导体的吸力最大值和斥力最大值相等，工频每过一周期，B相导体向A相导体、C相导体方向各摆动2次，如图2-11所示。
图2-11 作用在B相导体上的电动力
由式（2-89）和式（2-93）可知，B相导体受到的最大电动力是A相导体的最大电动力的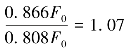
倍。
3.作用于C相导体的电动力
C相导体与A相导体完全对称，故C相导体受到的最大电动吸力和斥力与A相完全相同，只是最大斥力和吸力达到的时间有所不同。作用在C相导体上的电动力如图2-12所示。
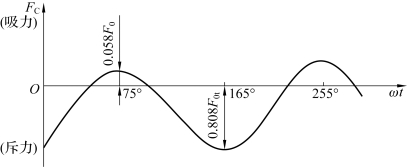
图2-12 作用在C相导体上的电动力
根据以上分析，可以得到以下结论。
当ωt=nπ+75°时，A相导体受到最大电动斥力，C相导体受到最大电动吸力；当ωt=nπ+165°时，A相导体受到最大电动吸力，C相导体受到最大电动斥力。A、C相导体受到的最大电动吸力和斥力不相等，最大吸力为0.058F0，最大斥力为0.808F0。
B相导体受到的最大电动吸力和斥力相等，分别发生在ωt=nπ+75°和ωt=nπ+165°，B相导体受到的最大电动力为A、C相导体受到最大电动力的1.07倍。因此，验算机械强度只要对B相验算即可。
无论是B相导体还是A、C相导体所受到的电动力都是交变的，其交变频率为电源频率的2倍，电动力的大小及方向均随时间变化。
为了避免三相直列布置的导体受力不均，有时将三相导体作等边三角形布置，如图2-13所示。根据同样的分析方法，可得A相导体受到的电动力为
式中：Fx和Fy为x方向和y方向的分力。
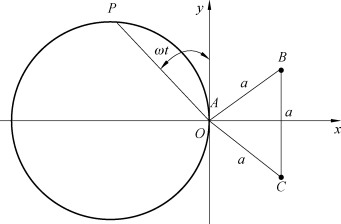
图2-13 三相导体作等边三角形布置
式（2-94）表明，A相导体受到的电动力其大小和方向随时间而变，可用
表示，
的端点随时间沿圆周移动。
B相和C相导体受到的电动力与A相完全相同，只是时间和空间上相位不同而已。
相关文章
- 详细阅读
-
焊接熔池动力学优化方案详细阅读
激光热传导焊时，金属材料只是在激光照射下产生熔化和形成熔池，熔池不出现明显的汽化现象。在这个区域，匙孔周围存在压力梯度和温度梯度。在压力梯度的作用下，熔化材料绕匙孔的周边由前沿向后沿流动。日本大阪大学接合所的Matsunawa等人所做的钨颗粒显示熔池流动的试验发现，在激光深熔焊的熔池中存在旋转的涡流构造，且能量较大，有强烈的搅拌力作用。......
2025-09-29
-
交流焊接电弧的特点与电特性详细阅读
交流焊接电弧一般是由50Hz按正弦规律变化的弧焊电源供电，电弧电流过零点及其电弧熄灭和引燃过程每秒出现100次。交流焊接电弧最大的特点是电弧周期性地熄灭和引燃。3）适当增大电流If，使电弧空间能量、热惯性增大，利于降低引弧所需电压，提高稳定性。......
2025-09-29
-
全电式炮控系统的交流特点详细阅读
交流全电式炮控系统的水平向和高低向系统都是由陀螺仪、调节器、永磁同步电动机调速系统和机械传动装置等组成。交流全电式炮控系统的最高瞄准速度为35°/s，最低瞄准速度为0.02°/s，调速比在1 750以上，远比传统炮控系统的高。传统炮控系统有12个部件，交流全电式炮控系统只有操纵台、控制箱、配电盒、水平向电动机、陀螺仪等6个部件，部件减少了一半。......
2025-09-29
-
全电装置可靠性优化方案详细阅读
早期的电传动技术没有达到大规模应用的水平，其原因主要包括：电传动装置的体积和质量大。电传动装置的能量效率差。现有的全电坦克炮控系统均采用电流环、速度环和位置环的三环结构。电动机的测速传感器得到的反馈速度和给定速度构成速度环，陀螺测量的反馈位置和操纵台设定的给定位置构成位置环。图2.1全电炮控系统组成原理框图......
2025-09-29
-
空载下行电源故障或安全回路失电时的制动力矩优详细阅读
2）对标准规范中限定的最大减加速度的情况下，最大的制动力矩要求：最大制动力矩式中 Sa_max——最大加速度下的最小制动距离，单位为m。......
2025-09-29
-
焊接过程电参数检测的优化方案详细阅读
焊接过程传感信号通常以电信号方式输出，电信号首先经过模拟电路进行预处理，然后经过数模转换为数字信号，再由微处理器或计算机系统加以监测和控制。图5-2-26 有源滤波器a）一阶有源滤波器 b）二阶低通滤波器4.信号转换电路传感器输出的电量形式有电阻、电感、电容、电流、电压、频率以及相位等多种形式，在焊接自动化系统中，通常需要对传感器输出的信号进行转换，以便达到系统控制所要求的信号，这就需要信号转换电路。......
2025-09-29
-
换相过程中输出电压的优化详细阅读
图2.34考虑交流侧变压器漏感时的三相半波可控整流电路及波形由于是电感性负载，负载电流id 近似为一条直线。例如从a 相换流到b相时，a 相电流从id 逐渐减小到零。这个过程称为换流过程。换流过程所对应的时间以电角度计算，称为换相重叠角，以γ 表示。当ia 减小至零、ib 增大至Id 时，换流过程结束，VT1 关断，VT2 完全开通。使整流输出电压平均值减小。......
2025-09-29
相关推荐