短路时的发热过程和热稳定性分析

2023-06-30 理论教育版权反馈

【摘要】：电路中的短路状态虽历时甚短，一般仅十分之几秒至数秒，但却可能酿成严重灾害。由于短路电流存在时间tscT，故其产生的热量尚来不及散往周围介质，因此短路过程是全部热量均用以使载流体升温的绝热过程。习惯上以短路持续时间为1、5、10 s时的热稳定电流I1、I5、I10表示电器的热稳定性。若母线正常工作时的温度θ0=55℃，试校核其热稳定性合格与否。它比允许温度200℃低，故母线的热稳定性为合格。

电路中的短路状态虽历时甚短，一般仅十分之几秒至数秒，但却可能酿成严重灾害。由于短路电流存在时间tsc≪T，故其产生的热量尚来不及散往周围介质，因此短路过程是全部热量均用以使载流体升温的绝热过程。若短路时间tsc≪0.05T，则

式中：τsc——长期通以短路电流Isc时的稳态温升。

　　 τsc按牛顿公式为

短路电流沿载流体截面作均匀分布，且其体积元dA dl内的发热过程遵循方程Pdt=cmdθ，即

经整理后再进行积分，得

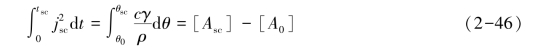
pagenumber_ebook=31,pagenumber_book=25

式中：jsc——短路时的电流密度；

　　 c、γ、ρ——载流体材料的比热容、密度和电阻率；

　　 A0、Asc——载流体的始、末截面积；

　　 θ0、θsc——短路过程始、末的载流体温度。

若已知c、γ、ρ和θ间的关系，而起始温度θ0又已给定，则函数[A0]和[Asc]均可求得，且可用曲线表示。它可用于进行下列计算。

（1）根据已知的短路电流、起始温度和短路持续时间，校核已知截面积的载流体的最高温度是否超过规定的允许温度。

（2）根据已知的短路电流、起始温度、短路持续时间和材料的允许温度，确定载流体应有的截面积。

以（1）中的方法对图2-5中的曲线进行计算的步骤如下。

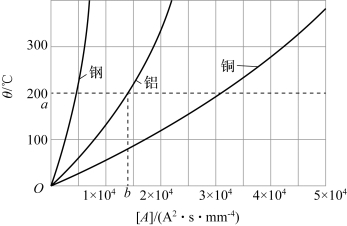
pagenumber_ebook=32,pagenumber_book=26

图2-5　确定[A]的值

（1）在纵轴上对应于载流体起始温度θ0的一点a作水平线，与曲线相交，再从交点作垂线交横轴于点b，从而得[A0]值；

（2）计算[Asc]值，即

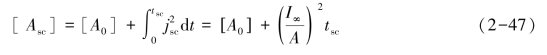
pagenumber_ebook=32,pagenumber_book=26

式中：I∞——短路电流稳态值（有效值）（A）；

　　 A——载流体横截面积（mm2）。

当tsc≤1 s时，取（tsc+0.05）为tsc的值。

（3）在横轴上对应[Asc]的点作垂线与相应材料的曲线相交，再自交点作水平线交纵轴即得θsc值。

在现实中是以热稳定电流衡量电器的热稳定性。热稳定电流是指在规定的使用条件和性能下，开关电器在接通状态于规定的短暂时间内所能承载的电流。电器的热稳定性以热稳定电流的平方值与短路持续时间之积表示。习惯上以短路持续时间为1、5、10 s时的热稳定电流I1、I5、I10表示电器的热稳定性。按热效应相等的原则，3种电流的关系为

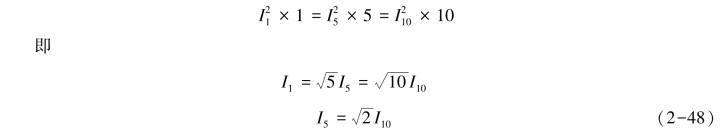
pagenumber_ebook=32,pagenumber_book=26

【例2-2】车间变电站低压侧的短路电流I∞=21.4 kA。母线为铝质，其截面积A=（60×6）mm2。短路保护动作时间为0.6 s，断路器分断时间为0.1 s。若母线正常工作时的温度θ0=55℃，试校核其热稳定性合格与否。

【解】对于图2-5中铝的曲线，当θ0=55℃时，有[A0]=0.45×104 A2·s·mm-4，短路过程结束时有

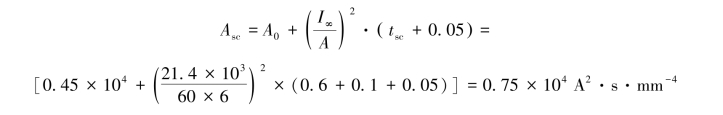
pagenumber_ebook=33,pagenumber_book=27

由图2-5中铝的曲线查得θsc=100℃。它比允许温度200℃低，故母线的热稳定性为合格。

短路时的发热过程和热稳定性分析

相关推荐