首页理论教育反复短时工作制的利弊分析与优化建议

反复短时工作制的利弊分析与优化建议

2023-06-30 理论教育版权反馈

【摘要】：因此，工作于反复短时工作制下的电器可能达到的温升将随着工作时间的增长而逐步升高，直至趋于某一稳定温升。

1.定义

当电器在通电和断电交替循环的情况下工作时，称该电器工作于反复短时工作制，电器通电和断电的时间均小于4T。

2.发热计算

设电器在一个工作周期内的通电时间为t1，断电时间为t2，工作周期为tp。根据电器反复短时工作制的定义可知，电器在第k个工作周期内所能达到的温升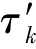 pagenumber_ebook=29,pagenumber_book=23 （对应于通电时间为t1末）将低于相同发热功率下工作于长期工作制时的最高温升（稳定温升），而在其断电时间为t2末的温升却大于0。换句话说，除了第一个工作周期外，电器在每个工作周期开始时刻的起始温升均大于0，而且下一工作周期的起始温升将高于前一工作周期的起始温升。因此，工作于反复短时工作制下的电器可能达到的温升将随着工作时间的增长而逐步升高，直至趋于某一稳定温升。

综上所述，在电器发热期间，电器的温升利用式（2-33）计算，而电器冷却过程的温升计算可以采用式（2-33），只不过需要考虑每个工作周期电器起始温升的变化规律。

设电器反复短时工作的功率为Pf。

1）工作周期1

电器发热过程的温升为

式中：τwf——发热功率；

　　 Pf——对应的电器稳定温升。

通电时间t1末时，电器的最高温升为

电器冷却过程的温升为

在该周期的断电时间t2末时，电器的温升将降至

2）工作周期2

电器发热过程的温升为

通电时间t1末时，电器的最高温升为

电器冷却过程的温升为

在该周期的断电时间t2末时，电器的温升将降至

3）工作周期k

以此类推，对第k个周期，通电时间t1末时，电器的最高温升达到τ′k，即

整理可得

断电时间t2末时，电器温升为

令第k个周期的温升 pagenumber_ebook=30,pagenumber_book=24 与长期工作的功率Pc所对应的稳定温升τwc相等，则可推得电器在反复短时工作制时的功率过载系数为

当tp≪T，且k→∞时，将式（2-38）中指数函数展开成级数，并忽略高次项，得

在电器标准中通常利用通电持续率TD%来描述反复短时工作制电器工作的繁重程度，即

显然，TD%值越大，工作周期内电器的通电时间就越长，其工作就越繁重。在极限情况下，如果TD%=100%，则该电器工作于长期工作制。如果tp≪T，则功率过载系数和电流过载系数与通电持续率的关系为