渗入深度z可通过试验前在试坑外3～4m处以及实验后在内环中心处,各钻1孔取土样,对比不同的岩(土)湿度的变化来确定。SL 345—2007《水利水电工程注水试验规程》在试坑双环注水试验中规定,土的渗透系数按式进行。坑内水头一般采用10cm;Hα为试验土层的毛细上升高度,cm,查表5-7得Hk后令Hα=2Hk,同样的,当0.5Hα值超过了试坑的开挖深度,应取试坑的深度值;z为从坑底算起的渗入深度,cm;16.67为单位换算系数。......
2023-09-18
电阻损耗及系数计算方法介绍
【摘要】： Kf是考虑交变电流趋肤效应和邻近效应对电阻的影响而引入的系数，即当导体中通过交变电流时，因趋肤效应和邻近效应而产生的附加损耗。则电阻损耗为式中：γ——材料的密度； m——材料的质量。电阻率ρ是温度θ的函数，其表达式为式中：ρ0、ρ20——0℃、200℃时的电阻率（Ω·m）； α、β——电阻温度系数。
电流通过导体所产生的能量损耗称为电阻损耗（或称焦耳损耗），其表达式为
式中：Kf——附加损耗系数。
Kf是考虑交变电流趋肤效应和邻近效应对电阻的影响而引入的系数，即当导体中通过交变电流时，因趋肤效应和邻近效应而产生的附加损耗。附加损耗系数Kf为趋肤系数Kj和邻近系数Kl之积，即Kf=Kj Kl，当导体中通过直流电时Kf=1。
趋肤效应是导体中通过交变电流时电流趋于表面的现象。图2-2所示为交变电流通过导体产生趋肤效应使导体内部电流分布不均匀的情况。阴影线所代表的导体截面中，导体内部（A部分）相连的磁通为Φ1和Φ2，导体外部（B部分）相连的磁通仅为Φ2。交变磁通在导体内感生反电动势，阻止原电流的流通，因中心部分反电动势比外表部分大，导致导体中心电流密度比外表部分小。
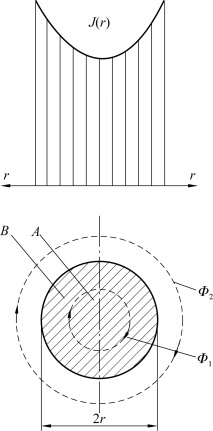
图2-2 趋肤效应影响下导体内部电流密度的分布
趋肤效应可以用电磁波在导体内渗入的深度b来表示，即
式中：ρ——导体材料的电阻率（Ω·m）；
μ——导体材料的磁导率（H/m）；
f——电流频率（Hz）。
趋肤系数Kj的计算公式为
式中：A——导体的截面积（m2）；
L——导体的周长（m）。
邻近效应是两相邻载流导体间磁场的相互作用使两导体内产生电流分布不均匀的现象。如果通过两相邻导体的电流方向相反，如图2-3（a）所示，则因一导体在另一导体相邻侧产生的磁场比非相邻侧产生的小，相邻侧感生的反电动势比非相邻侧小，故相邻侧的电流密度比非相邻侧的大；如果两相邻导体的电流方向相同，则相邻侧电流密度比非相邻侧小，如图2-3（b）所示。
邻近效应系数k1与电流的频率、导线间距和截面形状及尺寸、电流的方向及相位等因素有关，其值可以从相关的书籍及手册中查得。在一般情况下，邻近效应系数值也大于1。但也有例外，如较薄的矩形母线宽边相对时，邻近效应部分地补偿了趋肤效应的影响，故k1值略小于1。
图2-3 邻近效应影响下导体中的电流密度分布
（a）两电流异向；（b）两电流同向
若导体的电阻为
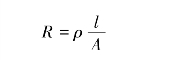
导体的电流为
式中：J——导体的电流密度（A/m2）；
A——导体的截面积（m2）；
l——导体的长度（m）。
则电阻损耗为
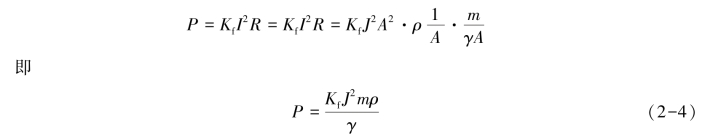
式中：γ——材料的密度（kg/m3）；
m——材料的质量（kg）。
电阻率ρ是温度θ的函数，其表达式为
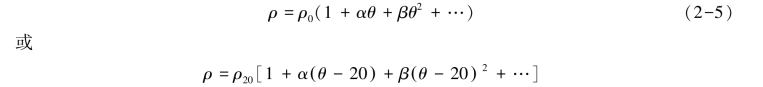
式中：ρ0、ρ20——0℃、200℃时的电阻率（Ω·m）；
α、β——电阻温度系数。
当θ≤100℃时，θ的高次项可以忽略，则上式可简化为
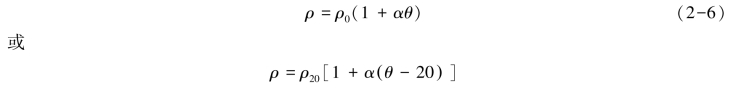
有关电器学的文章
- 详细阅读
-
散热系数的计算方法和影响因素：Nul数、导热详细阅读
在自由对流条件，对流散热系数可按式计算式中 Nul——努基尔数；λ——空气的导热系数；l——空气流过表面的长度。表5-3 公式中长度c、n和长度l的选择对流散热系数α是温度的函数，它随温度而变化。在热分析时，为了与对流散热的形式一致，将辐射散热通过表面散热系数简化为公式所示。因此，外表面的散热系数为α=αcon+αrad......
2023-06-15
-
「风速系数计算方法」在4.4.2节中的应用详细阅读
图4-9 风电机组的三维系数矩阵3）z轴为风速。取风速间隔为1m/s，根据风电机组的切入风速和切除风速的变化范围，把风速分为若干个区间。系数矩阵内每个元素CI是风电机组的风速系数。风速系数是以风电场输入风速为基准的，能反映场内每台风力机输入风速偏离风速基准值的大小，其计算框图如图4-10所示。以风电场输入风速为基准值，通过选择步长vstep、设定风速范围进行迭代计算，就可确定每台风电机组的风速系数。......
2023-06-28
-
力法典型方程与柔度系数计算方法详细阅读
根据叠加原理，式可写成以下形式：图14-12位移条件式就是为求解多余未知力X1和X2所需要建立的力法方程。对于高次超静定问题，其力法方程也可类似推出。当原结构在去掉多余约束处的已知位移为零时，其力法方程为方程中的系数称为柔度系数，位于主对角线上的系数δii称为主系数，在主对角线两侧的系数δij称为副系数，Δ1P称为自由项。由于基本体系是静定的，所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。......
2023-06-16
-
梯级链的设计、安全系数和使用寿命计算方法详细阅读
梯级链是自动扶梯最重要的驱动部件，各部件应按无限疲劳寿命进行设计，因此其安全系数最小为5。重载型扶梯一般要求采用安全系数为8的梯级链。梯级链受力计算 梯级链的受力通常需考虑乘客的载荷、梯级链的张紧力及梯级和梯级链自重等，下面介绍一种计算方法。梯级链的使用寿命主要取决于销轴比压，该计算以自动扶梯的制动载荷进行校核。......
2023-06-15
-
气体热传递系数实验及比较详细阅读
Eichelberg的研究 利用大型二冲程柴油机测量燃烧室内气体和壁表面的温度，发表了下述气体强制对流热传递系数的试验式。h0=0.2441/2v1/3p，m 式中，h0为气体热传递系数；p、T分别为气缸内压力和温度；vp，m为活塞平均速度，在全工作范围内不变。图8-11 各种气体热传递系数的经验式比较......
2023-06-28
-
极惯性矩Ip和抗扭截面系数Wp的意义和计算方详细阅读
极惯性矩和抗扭截面模量都是截面图形的几何性质，可以根据定义由积分法求出。AC 段和CB 段轴横截面的极惯性矩分别为计算应力。......
2023-06-19
-
高阶导数计算方法及例题详细阅读
y＝abxn即特别地，在式中取b＝1，有在式中取a＝e，有再在上式中取b＝1，有例3求y＝（1＋x）μ（μ∈R）的n阶导数.解当μN＋，则y′＝μ（1＋x）μ－1y″＝μ（μ－1）（1＋x）μ－2…......
2023-11-19
相关推荐