变压器工作原理详解

2023-06-30 理论教育版权反馈

【摘要】：图3-14所示为单相变压器工作原理。图3-14 一个双线圈的变压器工作原理图图3-14是一个双线圈的变压器工作原理图。变压器的负载阻抗为ZL。变压器能量的传递依靠的是主磁通，但是由于变压器的结构与制作等原因，往往会产生漏磁通，从而减弱了主磁通，使变压器的能量传递受到影响。

变压器是利用电磁感应原理，将一种等级的交流电压和电流变换为频率相同的另一种或几种等级交流电压和电流的电气装置。

1.变压器的基本工作原理

变压器由闭合铁心和两个或两个以上匝数不同、相互绝缘的线圈构成。图3-14所示为单相变压器工作原理。接到网络交流电源的线圈称为一次线圈或原边线圈、初级线圈，用“N₁”表示；连接负载的线圈称为二次线圈或副边线圈、次级线圈，用“N₂”表示。

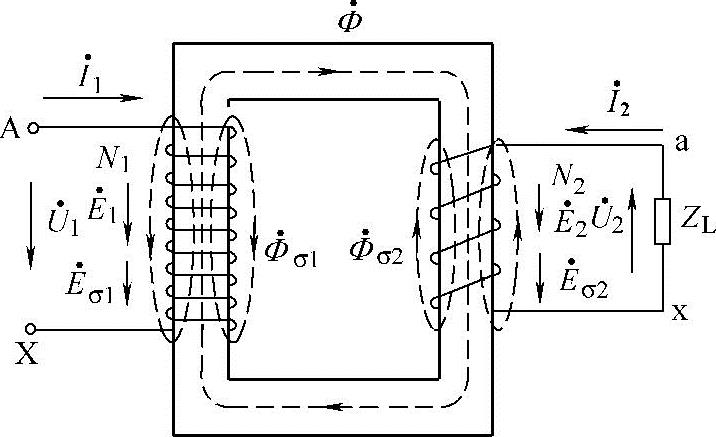
图3-14 一个双线圈的变压器工作原理图

图3-14是一个双线圈的变压器工作原理图。为便于分析，将一次和二次线圈分绕在铁心两侧（弧焊变压器经常采用此种结构），匝数分别为N₁、N₂。变压器的负载阻抗为Z_L。当一次线圈外加交流电源电压为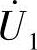时，便有电流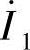流过一次线圈，在铁心中产生频率与外加电源电压频率相同的交变磁通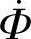，这就是“电生磁”。交变磁通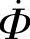的瞬时值Φ为：

Φ=Φ_msinωt （3-9）

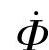同时交链变压器的一次、二次线圈，称为主磁通或工作磁通。根据电磁感应原理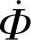，在N₁、N₂中分别产生感应电动势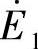、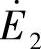，其大小与线圈匝数成正比，这就是“磁生电”。感应电动势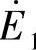、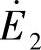的瞬时值分别是e₁、e₂：

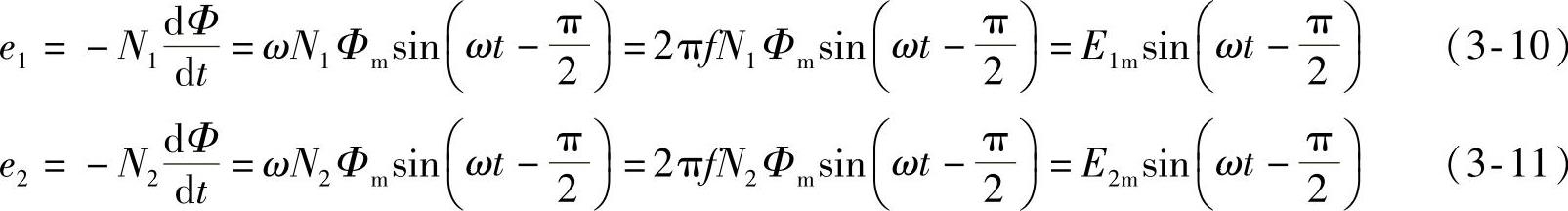
e₁、e₂的有效值E₁、E₂分别为

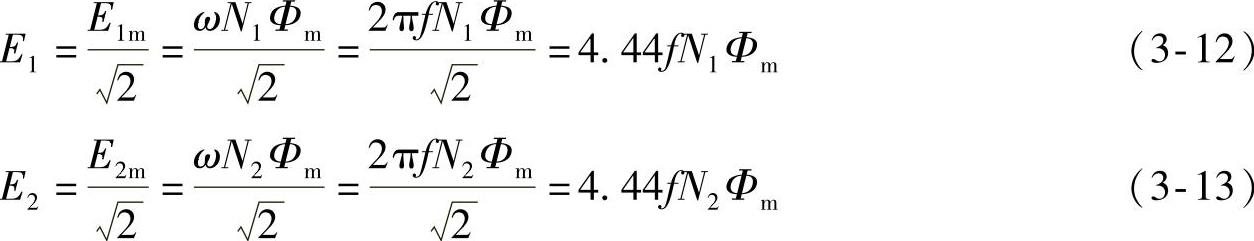
如图3-14所示，变压器工作时，除了主磁通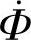以外，在一次、二次线圈中分别有一部分磁通经过空气闭合，这部分磁通被称为一次、二次线圈的漏磁通，分别用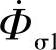、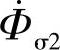表示。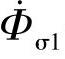仅与N₁相交链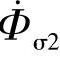，仅与N₂相交链。在变压器工作时，由于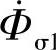、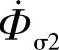的作用，在一次、二次线圈中分别产生漏感电动势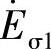、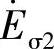，其作用是抑制电动势、。

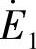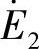根据电磁感应原理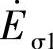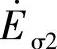，、的瞬时值分别是eσ1、eσ2：

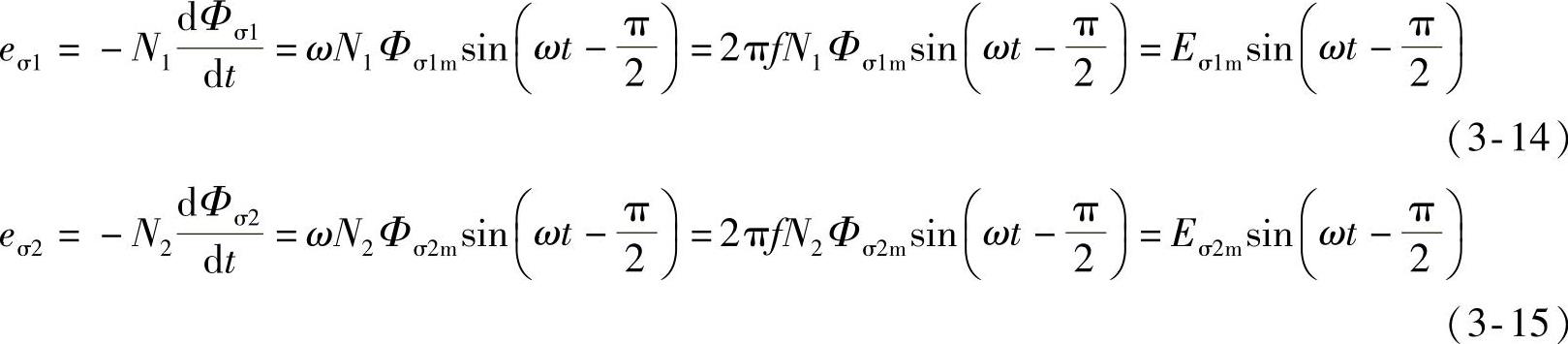
e_σ1、e_σ2有效值E₁σ、E_2σ分别为

E_σ1=4.44fN₁Φ_σ1m （3-16）

E_σ2=4.44fN₂Φ_σ2m （3-17）

感应电动势及漏感电动势的矢量表达式为

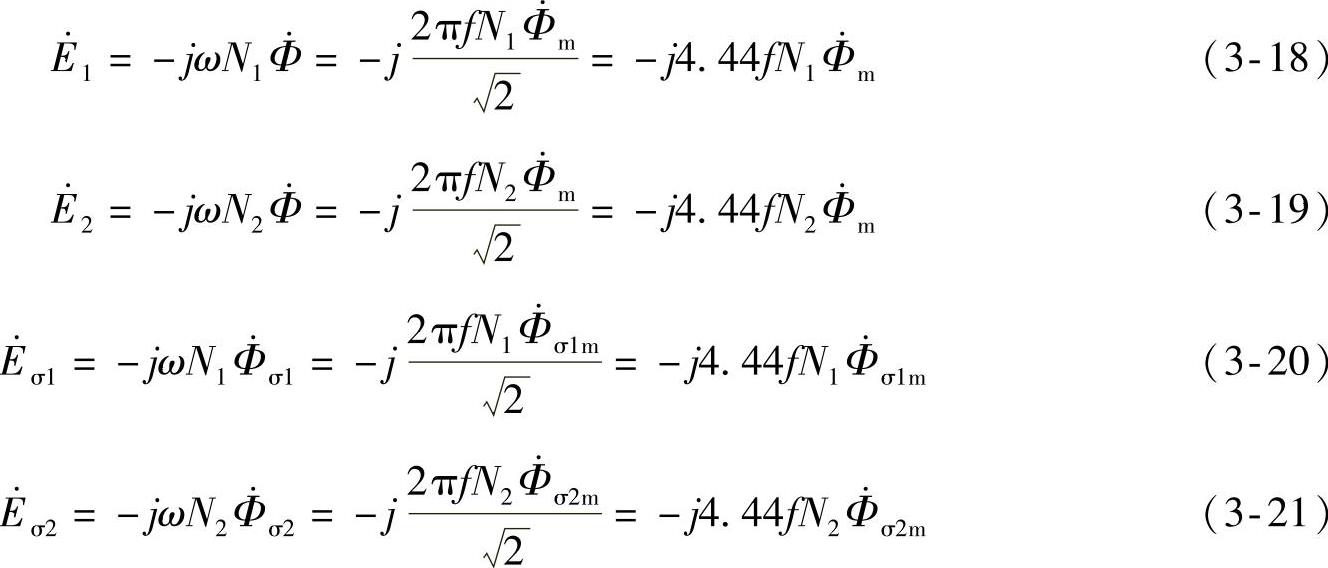
一般变压器铁心中的磁阻很小，漏磁路的磁阻基本上等于空气部分的磁阻。空气是非磁性物质，其磁导率是常数，漏磁路的磁阻可近似认为是一个常数。于是，漏磁通Φ·σ与所匝链线圈的电流大小成正比，且相位相同。因此，可以采用一次、二次线圈的漏电感系数L_σ1、L_σ2来表示漏磁通与电流之间的关系：

将L_σ1、L_σ2代入式（3-20）、式（3-21）中，可得

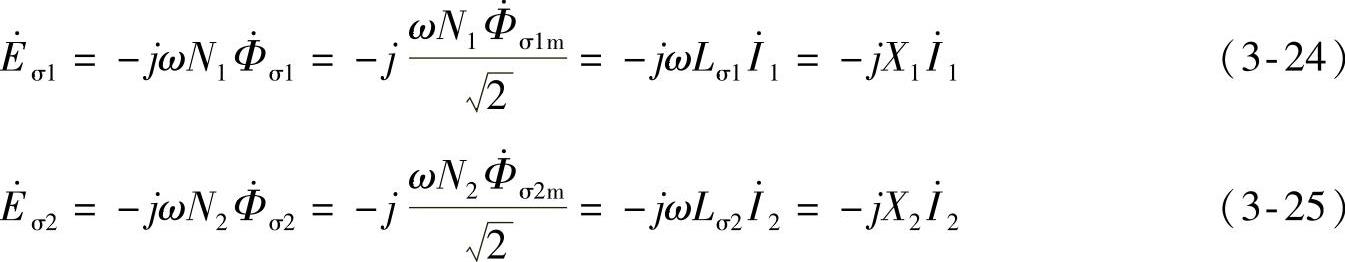
其中，X₁=ωL_σ1、X₂=ωL_σ2，分别是对应于一次、二次线圈的漏抗，单位为Ω。

一次线圈与二次线圈之间没有电的联系，只有磁联系，二次线圈产生的感应电动势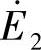

向负载Z_L供电，从而实现了电能的传递。

由式（3-12）、式（3-13）可见，如果变压器一、二次线圈的匝数不同，即N₁不等于N₂，则有E₁不等于E₂，即一、二次线圈产生的感应电动势不等。若忽略变压器一、二次线圈的漏阻抗压降，也可以说一、二次侧的电压不等，即为变压器的变压作用。

当变压器的负载阻抗为无穷大时，相当于没有连接二次负载，变压器处于空载运行状态，变压器二次输出电流为零，一次线圈中的电流为空载电流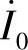；如果连接了二次负载Z_L，变压器处于负载运行状态，变压器二次线圈在感生电动势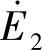作用下，产生负载电流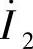，相应的一次线圈中的电流为。

2.变压器分析的理论基础

（1）变压器的电压比一次线圈与二次线圈的电动势之比称为变压器的电压比，以K表示。在变压器电磁作用实现电能的传递过程中，由于变压器一次、二次线圈匝数的变化，阻抗的影响等，使得一次、二次线圈的电压值等会发生变化，往往以变压器电压比K来反映这些变化。下式就是变压器的电压比的数学表达式：

电压比K是变压器的一个重要参数，当K＞1时，是降压变压器；当K＜1时，是升压变压器。

变压器能量的传递依靠的是主磁通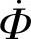，但是由于变压器的结构与制作等原因，往往会产生漏磁通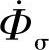，从而减弱了主磁通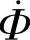，使变压器的能量传递受到影响。为了描述变压器磁耦合情况，提出了耦合系数k_M：

耦合系数k_M反映了一、二次线圈之间磁耦合的紧密程度，其值在0～1之间变化。k_M=1意味着Φ_σ1=0，即无漏磁通，耦合最好；k_M=0意味着主磁通Φ=0，完全漏磁，耦合最差。

（2）磁动势平衡方程式变压器空载运行时，变压器二次线圈开路，没有电流；只有变压器一次线圈中有电流流过，被称为空载电流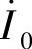，此时的磁动势为。

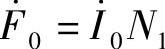当变压器负载运行时，作用在主磁路铁心上的磁动势有两个：一次线圈磁动势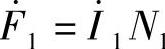和二次线圈的磁动势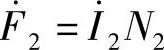，主磁通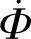是由这两个磁动势的合成磁动势所激励。

在变压器能量传递中，一次线圈上加载的交流电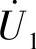产生磁动势，产生磁通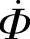。由于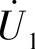不变是常值，相应的磁通也应保持不变。因此，变压器负载运行时的主磁通与空载运行时的主磁通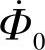基本相等。也就是说，变压器空载运行时的磁动势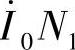与负载运行时的磁动势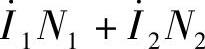应该相等，这就是所谓的磁动势平衡，下式就是变压器的磁动势平衡方程式：

将式（3-28）移项整理得

式（3-29）表明，变压器负载运行时，一次线圈中的电流由两部分组成，一部分为维持主磁通的励磁分量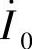；另一部分为用以补偿二次线圈磁动势作用的负载分量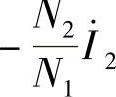。也就是说，变压器负载运行时，一次线圈中的电流I₁随着二次负载电流I₂的变化而变化。

（3）电动势平衡方程式变压器工作时，除了主磁通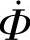以外，一、二次线圈分别流过电流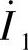、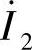，也会产生相应漏磁通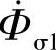、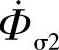以及漏感电动势、。

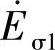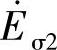按照图3-13所示的电压、电流和电动势的正方向，根据电路基尔霍夫定律，可列出变压器负载运行时一次、二次线圈的电动势平衡方程式：

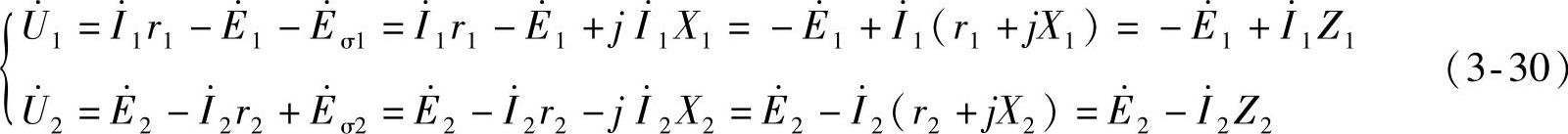
式中 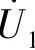——施加在变压器一次线圈上的网络电压（V）；

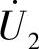——变压器二次线圈连接的负载Z_L上的电压（V）；

r₁、r₂——一次、二次线圈的等效电阻（Ω）；

X₁、X₂——一次、二次线圈的漏电抗（Ω）；

Z₁、Z₂——一次、二次线圈的漏阻抗（Ω）。

由此可见，当漏磁通非常小，漏阻抗Z₁、Z₂可以忽略的情况下，即k_M=1时，才有普通电力变压器中常用的电压比公式：

也可以得出该种情况下，电流I₁、I₂与线圈N₁、N₂之间的关系：

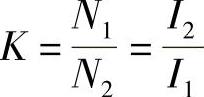
综上所述，可得变压器的基本方程式组：

（4）等效电路由于变压器的一次、二次线圈之间没有直接电的联系，仅有磁的耦合。虽然电磁平衡方程式可以反映其电磁关系，但计算十分繁杂。因此，希望有一个既能正确反映变压器内部电磁过程，又便于工程计算的单纯电路，来代替无电路联系、仅有磁耦合作用的实际变压器电路，这种电路称为变压器的等效电路。

变压器负载时的等效电路是将变压器一次、二次线圈的有关电参量放到同一个电路中进行分析的等效电路。

为了获得变压器负载运行时的等效电路，需要采用一定的折算方法，折算原则是折算前后磁动势、功率、损耗不变，即磁动势平衡关系、各种能量关系不变。

图3-15和图3-16所示是将变压器二次折算到一次的等效电路。其中，r_m、X_m、Z_m分别是变压器的励磁电阻（Ω）、励磁电抗（Ω）、励磁阻抗（Ω）；Z_m=E₁/I₀；r₂′、x₂′、z′_L是二次折算到一次的等效电阻、等效电感和等效负载阻抗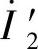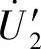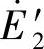；、、是二次折算到一次的等效电流、等效电压和等效感应电动势。

图3-16所示的等效电路被称为变压器的“T”型等效电路。

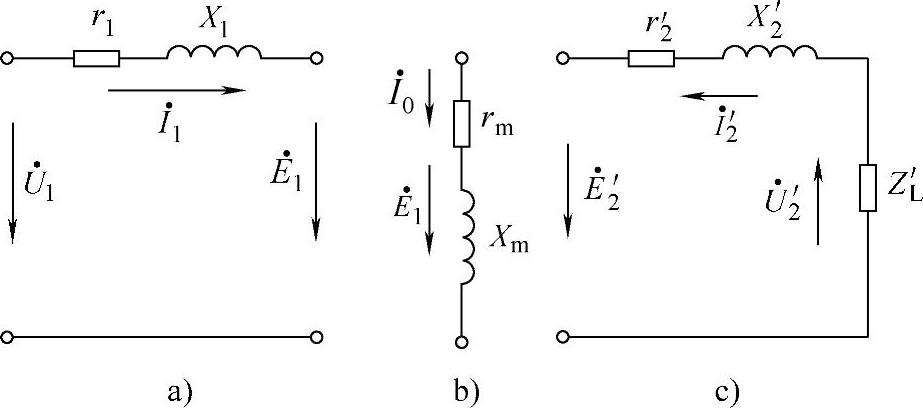
图3-15 变压器部分等效电路

a）一次线圈部分 b）励磁部分 c）二次线圈部分

图3-16 变压器“T”型等效电路

“T”型等效电路虽然客观地反映了变压器内部的电磁关系，但它是一个混联电路，进行复数运算较麻烦。普通的电力变压器中，I₀≈2%～10%I_1N（I_1N为变压器一次线圈的额定电流），因此，I₀往往忽略不计，即可以将励磁支路去掉，从而得到一个简化的串联电路，称为简化等效电路，如图3-17所示。

从图3-17可以看出，当二次侧短路，即Z′_L=0时，变压器的阻抗就是Z_k，故Z_k称为短路阻抗：

Z_k=Z₁+Z₂′=r_k+jX_k （3-33）

其中，r_k=r₁+r₂′，称为短路电阻（Ω）；X_k=X₁+X₂′，称为短路电抗（Ω）。

简化等效电路对应的电压平衡方程式为

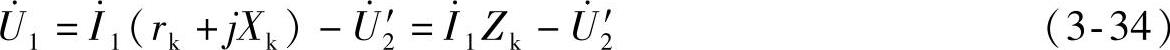
在弧焊电源的分析中，更多的是考虑负载变化时，变压器输出参数的变化，因此就要求将一次折算到二次的等效电路。

图3-18所示是将一次折算到二次的简化等效电路图，其中r″₁、x″₁是一次折算到二次的等效电阻和等效电感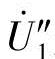；是一次折算到二次的等效电压；Z_L相当于电弧负载。

根据图3-18，可以列出其电压平衡方程式：

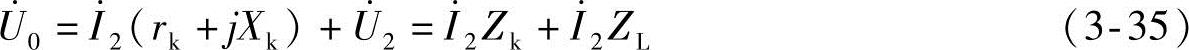
其中，r_k=r″₁+r₂、X_k=X″₁+X₂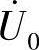；是变压器空载时的二次线圈的端电压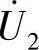；Z_k是变压器二次的等效阻抗：

Z_k=Z″₁+Z₂=r_k+jX_k （3-36）

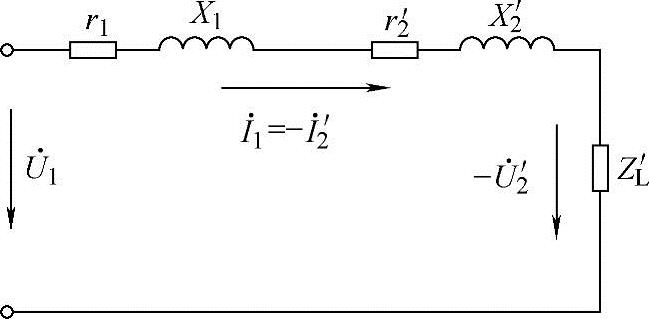
图3-17 变压器简化等效电路

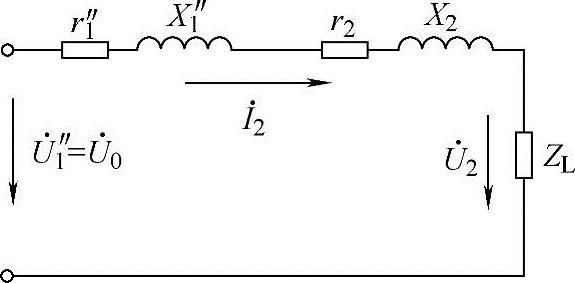
图3-18 一次折算到二次变压器简化等效电路

3.变压器的外特性

因为变压器的一次、二次线圈内部均存在电阻和漏抗，所以，当变压器工作时，即电流流过线圈时，内部的漏阻抗必然会产生压降，也就是说，即使一次线圈输入电压保持恒定，当变压器输出负载变化时，一次、二次线圈的电流会发生变化，变压器内部阻抗的压降也会发生变化，使得二次线圈输出的电压发生变化。

当一次线圈的输入电压U₁和负载功率因数cosφ₂（输出电压与电流相位差决定了负载功率因数cosφ₂）一定时，变压器二次线圈输出电压U₂随负载电流I₂变化的关系，称为变压器的输出特性，也称外特性，记作U₂=f（I₂）。其相应的曲线称为外特性曲线。

对于纯电阻或纯电感性负载，输入电压U₁和负载功率因数cosφ₂不变时，随着I₂的增加，U₂减小，变压器外特性曲线形状是下降的（见图3-19）。外特性下降的程度随cosφ₂的不同而有所差异，cosφ₂越小，变压器外特性曲线下降越快。

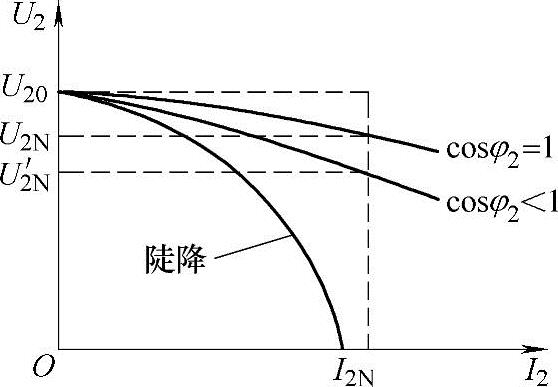
图3-19 变压器外特性曲线

变压器外特性下降程度与变压器内部的阻抗大小有关，变压器漏磁引起的感抗或变压器的内阻越大，外特性下降程度越大。变压器内部的阻抗将直接影响变压器外特性曲线形状。

对于普通的电力变压器、弧焊整流电源以及逆变弧焊电源中的变压器，要求其漏阻抗越小越好，因此其外特性曲线形状是平（或平缓）特性，而用于交流焊条电弧焊的弧焊变压器的漏抗较大，其外特性曲线形状是陡降的（或下降的）。

4.变压器的损耗与效率

（1）变压器的损耗变压器在传递能量的过程中，会产生损耗。变压器的损耗有铁损与铜损两大类。变压器空载运行时的损耗称为空载损耗，一般是指铁损；而变压器在额定情况下，负载运行时的损耗称为负载损耗，也称短路损耗，主要是指铜损。

变压器的基本铁损主要是磁滞损耗与涡流损耗。铁磁材料置于交变磁场中，被反复交变磁化，磁畴相互不停地摩擦而消耗能量，并以热量的形式表现出来，其损耗称为磁滞损耗。磁滞损耗与磁场交变的频率f、铁心的体积V和磁滞回线的面积成正比。

在变压器线圈中通交流电，根据安培环路定律，变压器铁心中产生的磁通量将是变化的。在交变磁场作用下，铁心内部会产生感生电动势，电动势在垂直于磁感应强度的平面上产生自成回路的电流i_w，称为涡流。涡流会使铁心发热，引起能量损耗，也就是涡流损耗。磁场交变的频率越高，磁通密度越大，则感应电动势就越大，涡流损耗也越大；铁心的电阻率越大，涡流所流过的路径越长，涡流损耗就越小。对于工频变压器来讲，其硅钢片的厚度越大，涡流损耗越大。

变压器的铁损还包括附加铁损。附加铁损产生的原因很多，主要如下：铁心接缝处由于磁通密度分布不均匀所引起的损耗；在变压器铁轭夹件、拉紧螺杆等结构部件中产生的涡流损耗等。附加铁损很难精确计算，通常对小容量变压器的影响较小，可以省略；而对大容量的变压器，各种附加损耗显著增加，甚至可达基本铁损的100%。

变压器的基本铜损是指一次、二次线圈内电流所引起的直流电阻损耗。附加铜损主要是由漏磁通所引起的趋肤效应和邻近效应，使电流在导线截面中分布不均匀而产生的额外损耗。

（2）变压器的效率η 变压器的效率一般是指输出功率与输入功率之比，即

式中 U_yI_y——变压器的输出功率（kW）；

P₁——变压器的输入有功功率（kW）。

（3）变压器的功率因数λ变压器的功率因数用λ表示（也有用cosφ表示的）。λ等于变压器从电源吸收的有功功率P₁与视在功率S_N之比。视在功率S_N等于变压器一次电流I₁与一次电压U₁的乘积，所以，变压器的功率因数λ为

变压器工作原理详解

相关推荐