在电磁铁结构尺寸和工作气隙值已知的情况下，直流磁路计算有以下任务。直流磁路计算可以采用分段法、漏磁系数法等方法。所分段数越多越接近于直流电磁铁的实际情况。图4-10拍合式直流电磁铁的磁动势及铁芯磁通图直流拍合式直流电磁铁示意图；线圈磁动势分态图；铁芯磁通图漏磁系数的定义及计算方法。......
2023-06-30
磁路及其计算方法
【摘要】：图3-3 磁路中的磁通用以激励磁路中磁通的载流线圈称为励磁线圈，励磁线圈中的电流称为励磁电流。若励磁电流为交流，磁路中的磁通是随时间变化的，这种磁路称为交流磁路。例如图3-5所示磁路由两段截面不同的铁磁材料和一段空气隙组成。值得指出的是，由于铁心饱和时磁路为非线性，因此铁心磁路计算时不能应用线性叠加原理。
1.磁路
磁通所通过的路径称为磁路。磁通的路径可以是铁磁物质，也可以是非铁磁物质。
如图3-3所示，变压器的线圈套装在铁心上，当线圈内通有电流时，线圈周围的空间（包括铁心内、外）就会产生磁场。由于铁心的导磁性能比空气要好得多，所以绝大部分磁通将在铁心内通过，这部分磁通称为主磁通。围绕着线圈，在部分铁心和铁心周围的空间，还存在少量分散的磁通，这部分磁通称为漏磁通。主磁通和漏磁通所通过的路径分别称为主磁路和漏磁路。
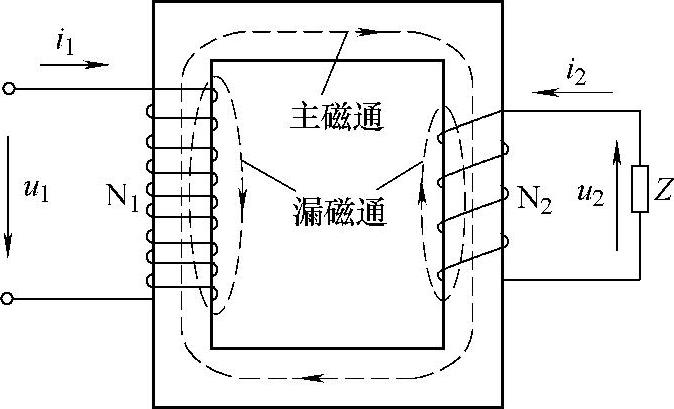
图3-3 磁路中的磁通
用以激励磁路中磁通的载流线圈称为励磁线圈，励磁线圈中的电流称为励磁电流。若励磁电流为直流，磁路中的磁通是恒定的，这种磁路称为直流磁路。若励磁电流为交流，磁路中的磁通是随时间变化的，这种磁路称为交流磁路。
2.磁路的基尔霍夫定律
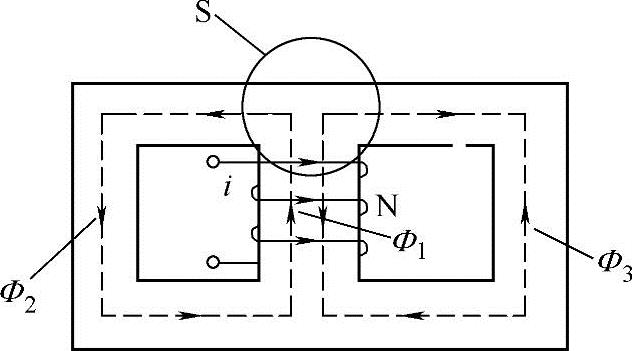
图3-4 磁路的基尔霍夫第一定律
（1）磁路的基尔霍夫第一定律 如果铁心不是一个简单回路，而是带有并联分支的磁路（见图3-4）。当中间铁心柱上有磁动势F时，磁通的路径如图中虚线所示。若令进入闭合面S的磁通为负，穿出闭合面的磁通为正，从图3-4可见，对闭合面S显然有
-Φ1+Φ2+Φ3=0
或 ∑Φ=0 （3-6）
式中 Φ1——穿过中间铁心柱的磁通（Wb）；
Φ2——穿过左侧铁心柱的磁通（Wb）；
Φ3——穿过右侧铁心柱的磁通（Wb）。
式（3-6）表明，穿出或进入任何一闭合面的总磁通恒等于零，这就是磁通连续性定律。该定律亦称为磁路的基尔霍夫第一定律。
（2）磁路的基尔霍夫第二定律 如果磁路由数段不同截面、不同铁磁材料的铁心构成，而且还含有空气隙。在磁路计算时，总是把整个磁路分成若干段，每段由相同截面积的相同材料构成，且假设段内磁通密度处处相等，磁场强度亦处处相等。例如图3-5所示磁路由两段截面不同的铁磁材料和一段空气隙组成。若铁心上的励磁磁动势为IN，根据安培环路定律（磁路欧姆定律）可得
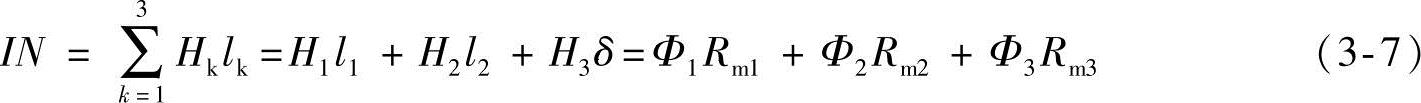
式中 l1和l2——1、2两段铁心的长度，其截面积分别为S1和S2；
δ——空气气隙长度；
H1和H2——1、2两段磁路内的磁场强度；
H3——空气隙内的磁场强度；
Φ1和Φ2——1、2两段铁心内的磁通；
Φ3——气隙内磁通；
Rm1、Rm2——1、2两段铁心磁路的磁阻；
Rm3——空气隙磁阻。
Hk是单位长度上的磁位降，Hklk则是一段磁路上的磁位降，它等于ΦkRmk。IN是作用在磁路上的总磁动势。式（3-7）表明了沿任何闭合磁路的总磁动势恒等于各段磁位降的代数和，这就是磁路的基尔霍夫第二定律。该定律实际上是安培环路定律的另一种表达形式。
值得指出的是，由于铁心饱和时磁路为非线性，因此铁心磁路计算时不能应用线性叠加原理。
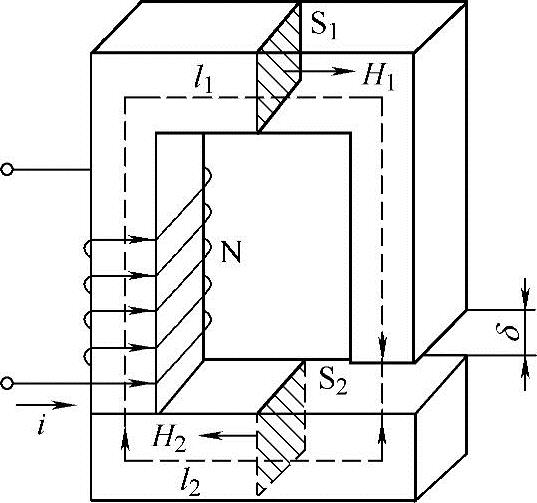
图3-5 磁路的基尔霍夫第二定律
有关现代弧焊电源及其控制的文章
- 详细阅读
-
永久磁铁磁路计算方法详细阅读
永久磁铁用于真空断路器、漏电保护断路器、节电型交流接触器及继电器电器中。磁系统中有永久磁铁，其磁通Φ1经铁轭、工作气隙、衔铁、铁芯成为回路，磁通Φ2经铁轭、分磁板、铁芯及空气隙成为回路，磁通Φ3是线圈产生的。永久磁铁的去磁曲线如图4-20所示。......
2023-06-30
-
电场强度及其计算方法详细阅读
一般常用检验电荷来探测、研究电场的性质。、nq，在A点所受到的电场力分别为F、2F、3F、…显然，F/q反映了电场中不同位置电场力的特性。检验电荷在电场中某一点所受电场力F与检验电荷量q的比值，称为该点的电场强度，简称场强，用公式表示为该计算值与假设值相近，说明假设的H3是正确的，表明1kg高压驱动蒸汽可以引射0.75kg的低压蒸汽；换言之，每引射1kg低压水蒸气需用1.33kg的驱动蒸汽。......
2023-06-20
-
力对点的矩及其计算方法详细阅读
力对点的矩是很早以前人们在使用杠杆、滑车、绞盘等机械搬运或提升重物时所形成的一个概念。若改变力的作用方向，则扳手的转动方向就会发生改变，因此，用F与d的乘积再冠以适当的正负号来表示力F使物体绕O点转动的效应，并称为力F对O点的矩，简称力矩，以符号MO表示，即O点称为转动中心，简称矩心。式中的正负号表示力矩的转向。分别计算图3-3所示的F1、F2对O点的力矩。......
2023-06-16
-
瞬态恢复电压及其计算方法详细阅读
本节将讨论单相单频回路，双频回路及三相电路开断的瞬态恢复电压。在绝大多数实际回路中，当断路器开断时，瞬态电压分别出现在断路器的两侧，瞬态恢复电压应是两个瞬态电压之和。在这些情况下，加到断路器两端的便是一个双频恢复电压瞬变过程，是电源侧和线路侧瞬态恢复电压的矢量差。通常只计算首开相的瞬态恢复电压。也可以在电网中进行实测，得出有关的瞬态恢复电压波形，但试验复杂，牵涉的问题很多，因而也很难进行。......
2023-07-02
-
环境监测中的采样效率及其计算方法详细阅读
采样方法或采样器的采样效率是指在规定的采样条件下所采集到的污染物量占其总量的百分数。用此法计算采样效率时，要求第二个采样管和第三个采样管污染物的浓度之和与第一个采样管比较是极小的，这样三个采样管污染物浓度之和就近似等于所配制的气体样品浓度。在空气监测中，评价采集颗粒物方法的采样效率多用质量采样效率表示。......
2023-11-23
- 详细阅读
- 详细阅读
相关推荐