【主要内容】1.函数微分的定义设函数y=f（x）在点x0的某个邻域内有定义.如果y在点x0处的增量Δy=f（x0+Δx）-f（x0） （其中，Δx是自变量x在点x0处的增量）可表示为Δy=AΔx+o（Δx）（其中，A与Δx无关，o（Δx）表示Δx→0时比Δx高阶的无穷小），则称y=f（x）在点x0处可微，称Δy的线性主部AΔx为y=f（x）在点x0处的微分，记为dy|x=x0（注意：函数y=f（x......
2023-10-27
层流边界层的微分方程式讲解
【摘要】：如果将这些控制微分方程根据边界层的特点进行简化，则经过简化的微分方程称为边界层微分方程。这里以稳态二维不可压缩流体流经平板时在边界层内的流动问题为例，说明其简化原则、简化过程以及简化后的微分方程式。1．原有的控制微分方程式2．连续微分方程的边界层理论简化3．y轴方向动量微分方程的边界层理论简化4．x轴方向动量微分方程的边界层理论简化11.3.3 简化结果
如同第1章内容提及，研究流体力学的主要目的之一是研究流体流场内部的运动参数变化以求得流体运动的基本规律，而在研究的过程主要讨论的是流体流速和压力的变化，所以在使用微分方程研究流体流动问题时，最常使用的控制微分方程为质量守恒微分方程和动量守恒微分方程，而在描述边界层内黏性流体运动的方程为 Navier-Stokes 微分方程（简称为N-S 方程）。如果将这些控制微分方程根据边界层的特点进行简化，则经过简化的微分方程称为边界层微分方程。这里以稳态二维不可压缩流体流经平板时在边界层内的流动问题为例，说明其简化原则、简化过程以及简化后的微分方程式。
11.3.1 简化原则
如图11-6 所示，均匀流体以u0流经平板，因为流体黏性效应，形成的边界层厚度越往下游越会增大。
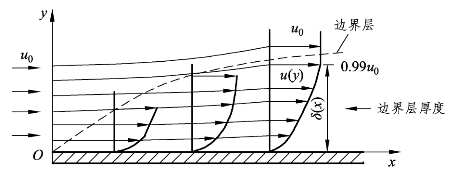
图11-6 平板边界层
相关研究证明，边界层的厚度非常细薄，可以得到边界层微分方程的简化原则，可以推知，边界层内流动的流体于x轴方向的速度u远大于y轴方向速度v，即u≫v以及边界层内流动的流体于y轴方向速度梯度变化远小于在x轴方向的梯度变化，也就是
。
11.3.2 简化过程
边界层微分方程的简化过程是将控制微分方程中的各项依据边界层微分方程的简化原则（u≫v与
）对原有的控制微分方程进行数量级大小的比较，保留主要项，忽略次要项，进行简化后得到边界层微分方程。
1．原有的控制微分方程式
2．连续微分方程的边界层理论简化
3．y轴方向动量微分方程的边界层理论简化
4．x轴方向动量微分方程的边界层理论简化
11.3.3 简化结果
有关工程流体力学基础的文章
- 详细阅读
-
泥沙的基本方程式详细阅读
10.4.1.2推移质不平衡输沙方程窦国仁推移质不平衡输沙方程式为:式中:γ和γs分别为水和泥沙颗粒容重;Hw和T 分别为平均波高和周期;根据多处海域资料求得α0=0.023，β0=0.04fw，fw为波浪摩阻系数;谢才系数用满宁公式确定，即C为床面糙率系数。......
2023-06-22
-
伯努利方程式：流动液体的能量方程式详细阅读
伯努利方程是能量守恒定律在流动液体中的表现形式。因而液体AB 段在Δt 时间流动时动能变化为:根据动能定理,外力所做功的总和等于液体能量的增量,即故有:将上式两边分别除以Δmg,整理得:或式和式称为理想液体的能量方程,一般称为理想液体的伯努利方程。式称为实际液体的伯努利方程。......
2023-06-18
-
变压器的运行方式讲解详细阅读
因此，自然循环冷却变压器的顶层油温一般不宜经常超过85℃。当冷却介质温度低时，油浸式变压器顶层油温也相应降低。干式变压器的温度限值应按制造厂的规定。......
2023-06-24
- 详细阅读
-
拥吻礼仪与各种常见形式的讲解详细阅读
在人们表示慰问、祝贺、欣喜时,拥吻礼也十分常用。拥吻礼在我国的涉外活动中也很常见,它包括亲吻、拥抱和吻手三种。亲人、熟人之间见面多是拥抱、亲吻。(二)拥抱礼拥抱礼是欧美各国熟人、朋友之间表示亲密的一种礼节,常常与亲吻礼同时施行。行正规的拥抱礼时,两人正面面对站立,各自举起右臂搭在对方的左肩后面；左臂从下方扶在对方右腰后侧。(三)吻手礼吻手礼是主要流行于欧美上流社会异性之间的一种最高层次的见面礼。......
2023-07-03
-
圆管中的层流运动及其影响因素详细阅读
如图1-13所示，液体在一直径为d的圆管内做层流运动，即Re＜Rexp=2320。图1-13 圆管中的层流在液流中取一小圆柱体，小圆柱体的直径为2y，长度为l，并设液流从左向右流动。......
2023-06-15
-
超文本和超媒体概念的讲解详细阅读
超文本和超媒体的概念与多媒体密切相关，因此很容易把它们和多媒体混淆在一起。由图5.1可以看出超文本具有包含多种媒体信息、网络结构形式和交互性三大特点。图5.1超文本的概念图超文本不是顺序的，而是一个非线性的网状结构，它把文本按其内部固有的对立性划分成不同的基本信息块，称为“节点”。早期的超文本的表现形式仅仅是文字的，这就是它被称为“文本”的原因。......
2023-10-22
相关推荐