根据物质被磁化后对磁场所产生的影响，可把物质分为三类：使磁场减弱的物质称为抗磁性物质；使磁场略有增强的称为顺磁性物质；使磁场急剧增加的称为铁磁性物质。原子核也有磁矩，不过它的磁矩很小，约为电子磁矩的1／2 000，故通常情况下可不予考虑。上述表明，电子是有磁矩的，电子的磁矩是轨道磁矩与自旋磁矩的矢量和。只有原子存在着未被排满的电子层时，由于电子磁矩之和不为零，原子才具有磁矩。这种磁矩称为原子的固有磁矩。......
2023-06-20
边界层基本概念介绍
【摘要】：图11-1 内黏滞流场与外黏滞流场之间边界层差异边界层理论是理论求解黏性流体外部流动的主要方法之一，尽管前面第4章的内容已有说明，但是为了本章内容的连贯性以及加速对本章内容的理解，这里对其特性再做重点的描述，强调重点在于边界层厚度的概念、镶合理念处理模式以及吹除厚度和动量厚度的定义等。
实际流体都有黏性，在运动中必然会出现一些与理想流体不同的规律，这种差异性一般限于紧贴物体表面，且在黏性作用不可忽略的流体薄层内，此薄层即称为边界层（Boundary layer）。从第4章的内容来讲，边界层理论概念于 1904年由普朗特提出。对于雷诺数Re较大的黏性流体流动可以看成由两种不同形态的流动组成：一种是边界层内流体的流动，流体的黏滞作用不可以忽略不计，也就是必须把流体当作黏性流体来做考虑；另一种形态的流动则是指边界层以外的流体流动，流体黏滞效应的效应可以忽略不计，也就是可以将边界层外的流动流体视为非黏性流体。这种处理黏性流体流动的方法为近代流体力学的发展开辟了新的途径，大大地简化问题研究的复杂度和计算的难度。研究流体流动问题时可以根据观察流体流场的位置将流场分成内部与外部流场两种类型问题，内部流场问题通常是指流体在管道内的流动问题，例如流体在发动机内的流动或者流体在管路中的流动，外部流场则是指流体流经物体表面的外部流动，例如飞机在大气中飞行，气体在飞机外部的气流性质变化。和内黏滞流场不同的是，内黏滞流场内，黏滞边界层越往下游越厚，不久就弥漫于整个流场，黏性效应会主导整个流场内的流动状况，而外黏滞流场中边界层在理论上可以无限地延伸，只有在边界层外的流动才视为非黏性流动。内黏滞流场与外黏滞流场两者边界层的差异如图11-1所示。
图11-1 内黏滞流场与外黏滞流场之间边界层差异
边界层理论是理论求解黏性流体外部流动的主要方法之一，尽管前面第4章的内容已有说明，但是为了本章内容的连贯性以及加速对本章内容的理解，这里对其特性再做重点的描述，强调重点在于边界层厚度的概念、镶合理念处理模式以及吹除厚度和动量厚度的定义等。
11.1.1 概念说明
如图11-2所示，以流体流经平板为例说明边界层代表的物理现象。虚线是代表边界层，在边界层的内部必须考虑流体流场的黏性，在边界层的外部可以将流体流场的黏性效应忽略不计。此外，流体与平板间形成的边界层随着流体流经平板的距离逐渐增厚，这是由于流体流经平板的距离（x轴方向的距离）越长，流体所受到黏性影响越大的缘故。
图11-2 边界层概念
11.1.2 边界层厚度的定义
为了区分黏性流区域与非黏性流区，必须对边界层的厚度进行定义，以流体流经平板的外部流动来说明，如图11-3 所示表示均匀流体以等速度u0流经平板的速度变化。流体在边界层内的流体流速为u(y)，y为流体质点与固定表面的垂直距离。当边界层内流体的流速达到99%u0时，在y轴的位置δ，则可以假设δ以外的区域为非黏性流区，而δ即为边界层的厚度。流体不受到流体黏性影响的速度为自由流速度u0，所以边界层厚度的定义可以表示为u (δ)=0.99u0。一般而言，在流体流场与固定表面的垂直距离y大于或等于边界层厚度δ时，都假设流体的流速不会受到流体黏性影响，也就是假设 u(δ)=u0。边界层厚度的定义和前面提及的无滑流现象，也就是u(0)=0一样，在流体力学与空气动力学的问题研究中，主要当成黏性流体流速的边界条件之一。
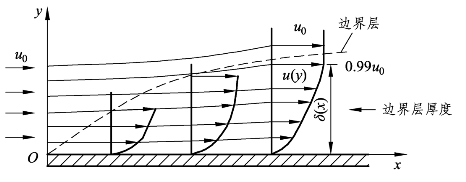
图11-3 边界层厚度定义
11.1.3 镶合理念处理模式
边界层理论的概念提出为近代流体力学的发展开辟了新的途径，研究中，可以先求出边界层内部黏滞区域内流场运动参数，例如流体流速和流体性质等物理量的变化，然后再将其和边界层外部非黏滞区域内流体流场运动参数的变化情形镶合起来，即可求出整个外部流场运动参数的变化，这种处理模式称为镶合理念处理模式（Combination concept processing mode）。相关研究指出，这种处理模式在流体雷诺数Re越大时，镶合所得的结果就越精确。但是对于雷诺数Re很小的流场，由于黏性流区域与非黏性流区之间的相互作用相当强烈，而且其间变化趋势为非线性，流体流场的运动参数稍有变化，就会造成边界层内部的流场，也就是流体流场黏滞区域内压力分布大幅地变化。因此如果流体流场的雷诺数非常小，镶合理念处理模式可能并不适用。此外，气体发生流体分离现象时，产生气体回流，边界层理论也不适用。
11.1.4 吹除厚度的定义
从图11-3中可以发现，流体流动因为边界层效应的影响而造成外围流线的微小位移称为吹除厚度（Displace thickness）。如图11-4 所示，在边界层中，实际流体流动的质量流率为
而对于相同质量流率的非黏性流体的质量流率
在实际流体流动与非黏性流体在流动质量流率相同的情况下，两者在固定表面的垂直距离之间的差值即称为吹除厚度，用符号 δ*表示，其数学定义为，当
时，δ* =δ- h。式中，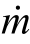
、ρ、u0、u、 b、δ *和δ分别为流体的质量流率、流体密度、均匀流的流速、流体质点的流速、边界层宽度、吹除厚度与边界层厚度。由于边界层非常细薄，也就是边界层的厚度非常小，流体流动会因为边界层效应产生流线位移，也就是吹除厚度对外围无黏流场造成的影响一般可以忽略不计，因此在边界层理论处理黏性边界层内部流场问题时，边界层外围的压力场推动边界层流动，其作用就有如动量方程的外力函数。
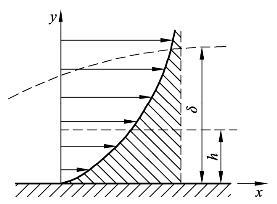
图11-4 吹除厚度定义的示意图
11.1.5 动量厚度的定义
有关工程流体力学基础的文章
- 详细阅读
-
平板边界层的计算的分析介绍详细阅读
表11-1 常用外部流动的层流公式11.4.2 平板湍流边界层的计算公式对于在临界雷诺数以下的流体流动状态为层流，超过临界雷诺数的流动状态视为湍流边界层。根据实验发现，只要不发生显著的分离现象，曲面情形的摩擦阻力和平板情形差不多，所以平板湍流边界层的研究结果可用于近似计算船体、机翼、机身、叶轮机械叶片的摩擦阻力。......
2023-06-29
-
非织造布：基本概念和应用介绍详细阅读
（一）堤段概况九江市城防大堤位于长江微弯河道的右侧一级阶地，溃口段位于桩号1+813～1+875m处，见图1-6。图1-6九江市城防大堤溃口段位置示意图堤顶高程23.72～23.75m，顶宽4.7～5.8m，底宽9～12.5m。堤外侧为直立的浆砌石挡墙，厚0.5m及厚0.2m的钢筋混凝土防渗墙，墙顶高程25.25m，墙底高程22.14m，墙底与外侧混凝土护坡相连，护坡下端设有深1m，厚0.2m的防渗齿槽。堤内侧有直立的浆砌石挡墙，高约2m，顶宽0.6～0.7m，底宽2.1m。......
2023-06-20
-
基本概念和特点详细阅读
空间信息网络是以空间平台为载体，实时获取、传输和处理空间信息的网络系统，其基本构成如图1-1所示。其节点包含各种卫星、空间站、升空平台、有人或无人机，这些平台节点在业务性质、应用特点、工作环境、技术体制等方面均有差异，由此构建的网络具有网络异构和业务异质的典型特征。图1-1空间信息网络架构图1-2空间信息网络的特点......
2023-07-02
-
热辐射现象基本概念详解详细阅读
发射辐射能是各类物质的固有特性。显然，热辐射是电磁波传递能量的现象。通常把波长在0.1～100μm范围的电磁波称为热辐射。于是有α+ρ=1 当热辐射投到气体上时，由于气体对辐射能几乎没有反射能力，则可认为ρ=0。于是有α+τ=1 热辐射投射到物体表面后的反射现象有镜面反射和漫反射两种类型，区分反射类型取决于物体的表面粗糙度。......
2023-06-23
-
微分方程基本概念详细阅读
引例例1 已知曲线上任一点的切线斜率等于该点横坐标的两倍，试建立其方程.解 所求曲线应满足方程例2 质量为m的物体只受重力的作用自由下落，试建立其路程s与时间t的关系.解 把物体降落的铅垂线取作s轴，其指向朝下（朝向地心）.设物体在t时刻的位置为s=s（t），加速度.由牛顿第二定律F=ma，得这是由著名科学家伽利略研究发现的，自由落体的重力加速度为常数g.例3 某商品在t时刻的售价为P，社会对该商......
2023-11-22
-
理解报警系统基本概念详细阅读
自定义报警是在HMI设备上组态的由PLC的过程数据引起的报警，包括离散量报警和模拟量报警。离散量报警对应于二进制数的1位，离散量的两种相反的状态可以用1位二进制数表示。离散量报警由变量内的某个位触发报警，而模拟量报警则由变量的限制值触发报警。该报警类别不需要进行确认。报警窗口的关闭和重新打开均可通过事件触发。......
2023-06-15
-
文件管理基本概念讲解详细阅读
1．文件文件是一组逻辑上相互关联的信息集合，可以是文档、图片、歌曲、视频等。文件名通常由两部分组成，即主文件名和扩展名，中间用分隔符“.”连接。其格式为：Windows文件的命名必须遵循以下约定：① 支持长文件名，但总长度不超过256个字符。③ 允许使用多间隔符，最后一个分隔符“.”后面的内容是扩展名。④ 文件名可以包含汉字、字母、数字、下划线、空格及一些特殊字符，但不可以包含？......
2023-11-01
相关推荐