图10-5 不可压缩流体在圆管内做均匀层流运动10.5.2 流体流场的速度分布情形圆管层流的最大速度umax为于r=0处,其计算公式为。......
2023-06-29
在实际工程上常见的流动多为湍流状态,例如一般管道内的流速 V= 3~5 m/s ,水的运动黏度ν=10×10 - 6 m2/s ,管径 d= 0.1 m ,则流体的雷诺数 Re= 3×105 ~5×105 m/s ,此时水在圆管内的流动状态很显然是湍流运动,因此湍流的特征和运动规律在解决工程实际问题中具有非常重要作用。
10.7.1 雷诺时间平均概念
流体在圆管道内做湍流运动时,由于湍流质点相互碰撞与混杂,使得流体质点的速度随着时间不断变化,造成流体流场各空间位置点的速度和压力等流动参数也随着时间作无规则变化,研究湍流管流问题有着极大的难度。然而实践证明,在空间中某一位置点的流速和压力等流动参数,虽然时刻都会发生变化,但在一个较长的时间内,这种变化并不漫无边际,而是围绕某一平均值做上下波动,如图10-9所示。这种现象称为湍流的脉动现象(Pulsation phenomenon),平均值即为时间平均值(Time average value或time mean value),简称时均值。
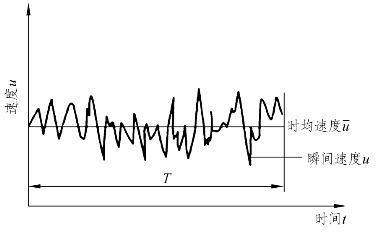
图10-9 流体在管道内做湍流运动时的瞬时速度变化曲线
湍流具有脉动现象的特性,再加上工程计算中关心的是流体流动参数对时间的平均变化情形,所以雷诺在 1845年提出了雷诺时间平均的概念,并为湍流的平均速度和平均压力做了如下的定义。
1.时间平均速度的定义

2.时间平均压力的定义

基于时均值的概念,可以将湍流简化成时均流动和脉动流动的迭加,这样对时均流动和脉动流动分别进行研究。工程实践上,关注的多为流体运动参数的时间值变化,所以只需研究各运动参数的时均值变化,也就是使用运动参数的时均值来描述湍流运动,此时描述的湍流就称为时均湍流。但是如果研究湍流具备的物理现象,例如湍流阻力的形成机制,就必须考虑湍流脉动造成的影响,也就是不可以使用运动参数的时均值来描述湍流的运动。除此之外,虽然湍流运动总是非稳态的流动,但是工程上常将运动参数的时均值作为湍流的运动参数,如果当湍流运动参数的时均值不随着时间变化而改变时,则湍流可以认为是稳态流动,此时湍流的运动状态称为时均稳态湍流。在工程业界讨论湍流时稳态流动指的就是时均稳态湍流。对于研究这种湍流,前述内容使用的连续性方程式、伯努利的修正方程均可适用,而本书在其后内容讨论的湍流均为时均湍流,且为稳定流动。
10.7.2 圆管内的湍流结构
如图10-10所示为流体在管道内的湍流结构示意图,从图中可以看出,湍流结构分成黏性底层、过渡层以及湍流核心区等结构。实验证明,流体在管内作湍流运动时,并非整个管流都是湍流。在贴近管壁的地方会有非常薄的一层流体由于管壁的阻碍作用,速度很小,流体的运动处于层流运动状态,该流层称为层流底层(Laminar bottom layer)或黏性底层(Viscidity bottom layer)。在管道中心的部分流体受到管道壁面的影响较小,流体质点的碰撞频繁,流体的运动表现出明显的湍流特征,该部分称为湍流核心区(Turbulent core area)。而在湍流核心区与层流底层之间是一层很薄的不完全湍流区,该区城又称为过渡层(Transition layer)或缓冲层(Buffer layer)。
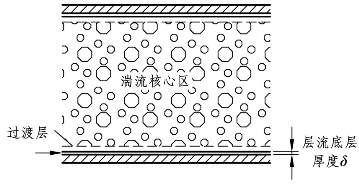
图10-10 流体在管道内流动时的湍流结构
层流底层厚度(δ)随雷诺数的增大而减小,也就是湍流越强烈,雷诺数越大,层流底层越薄。层流底层厚度一般只有几十分之一到几分之一毫米,但它的存在对管壁粗糙的扰动和传热性能有重大影响,因此不可忽视。对于直径为d的圆形管道,层流底层的厚度δ可以用半经验公式![]() 计算,式中,Re与f分别为管流的雷诺数与沿程阻力系数。
计算,式中,Re与f分别为管流的雷诺数与沿程阻力系数。
10.7.3 水力光滑管和水力粗糙管的判定
由于材料性质、加工条件、使用条件和年限等因素的影响,任何管道的内壁都不可能绝对光滑,总会有凹凸不平现象,在工程上,管壁表面上凹凸不平的平均尺寸称为管壁的绝对粗糙度(Absolute roughness),用符号△表示。绝对粗糙度△与管径d之比值△/d称为管壁的相对粗糙度。根据层流底层厚度δ与相对粗糙度△/d的相互关系,将管道分为水力光滑管和水力粗糙管两种管道,如图10-11所示。

图10-11 水力光滑管和水力粗糙管的外形
实验与理论研究均已证明,如果层流底层厚度δ远大于相对粗糙度△/d,管道内壁凹凸不平处会完全被层流底层掩盖,所以管壁的粗糙度几乎对管道内流体的流动无影响,就相当于流体在光滑管内流动,可认为沿程阻力损失和管壁粗糙度无关。此时的管道就称为水力光滑管(Hydraulically smooth pipe)。如果层流底层厚度δ远小于相对粗糙度△/d,管道内壁凹凸不平处会全暴露于湍流核心区中,此时湍流核心区的流体能够直接和粗糙壁面接触并冲击管道内壁的凹凸不平处形成涡旋,从而使得能量损失急剧增加。此时管壁的粗糙度成为沿程阻力损失的主要影响因素,因此该种管道就称为水力粗糙管(Hydraulically rough pipe)。据此,工程定义如果![]() 则该管道称为水力光滑管;如果
则该管道称为水力光滑管;如果![]() 则该管道称为水力粗糙管;如果
则该管道称为水力粗糙管;如果![]() 此时管道内流体虽然开始受管壁粗糙度的影响,但还未对湍流核心区的流体产生决定性的作用,流体在该管道的流动状态称为水力光滑管到水力粗糙管之间的过渡状态。
此时管道内流体虽然开始受管壁粗糙度的影响,但还未对湍流核心区的流体产生决定性的作用,流体在该管道的流动状态称为水力光滑管到水力粗糙管之间的过渡状态。
10.7.4 湍流剪应力组成及分布情形


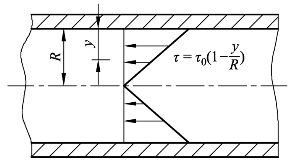
图10-12 圆管湍流剪应力分布情形的
10.7.5 湍流的速度分布情形
如图10-13所示为圆管中不同雷诺数Re时的速度分布情形,湍流的速度分布与层流的速度分布有很大的区别。层流(Re< 2 320)的速度剖面是一个旋转抛物面,随着Re的增大,壁面附近的速度梯度逐渐增大,在轴线附近一个较大的范围内,速度变化很平缓,湍流剪应力集中分布于壁面附近。湍流速度结构分成黏性底层、过渡层以及湍流核心区三个部分。在黏性底层,流体为层流状态,剪应力主要为黏性剪应力,惯性剪应力可以忽略不计;在湍流核心区内,惯性剪应力占据着主导的地位;在过渡区,黏性剪应力和惯性剪应力具有同一个数量级,但过渡区很小,一般将其并入湍流核心区来处理。

图10-13 圆形管流在不同雷诺数时的速度分布情形
1.黏性底层的速度分布情形

2.湍流核心区的速度分布

从图10-14 中可以看出圆管湍流在湍流核心区的速度梯度较小且分布较均匀,这是由于湍流核心区中流体质点脉动混掺发生强烈动量交换造成的。将速度分布公式代入动能修正系数与动量修正系数的计算式中,可求出圆管湍流的动能修正系数α≈ 1.0以及动量修正系数β≈1.0。
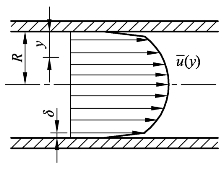
图10-14 圆管湍流在管内的速度分布情形
有关工程流体力学基础的文章

图10-5 不可压缩流体在圆管内做均匀层流运动10.5.2 流体流场的速度分布情形圆管层流的最大速度umax为于r=0处,其计算公式为。......
2023-06-29

湍流的重要特点是物理量的脉动,目前描述湍流流动的数值模拟方法主要包括直接数值模拟、大涡模拟和分离涡模拟等。分离涡模拟方法是将大涡模拟和雷诺平均方法结合,在壁面处采用分离涡模拟方法,在湍流的核心区域采用大涡模拟方法。模型考虑了网格的各向异性,且调整亚网格长度尺度来实现RANS向LES的过渡。除此之外,为解决近壁雷诺应力估计不足的问题,IDDES模型中增加新项fe。......
2023-06-23

瑞士数学家L.欧拉大约在200多年前提出了以下两种描述流体运动的方法。拉格朗日方法采用动坐标,注意于每一流体质点的运动历史;欧拉方法采用定坐标,注意于液体运动时每一空间点处流体状态的变化。在渗流力学中通常会采用欧拉方法来描述流体运动过程中的质量、动量和能量等。......
2023-06-28

通常在研究流体力学问题时,主要是研究流体在静止或运动时流场的性质或运动参数的变化以及流体运动的基本规律。一般而言,研究流体力学问题的方法大概可以分成理论解析法、实验观测法以及数值计算法。其优点在于研究费用较少,可以计算复杂的流体流动问题,计算结果也与真实现象之间的偏差较小。......
2023-06-29

实验中的故障电流是利用单频振荡回路提供的,主要是将大型电容器组充电后使之对电感放电以产生工频电流。实验开始前,S1打开,通过整流器对电容器组Ci充电,当达到实验所需的电压后,断开充电电路,即可开始实验。图2-14 实验电路图图2-15是预期电流10kA时对断路器进行实测的短路试验波形,图中通道CH1、通道CH2和通道CH3分别为短路电流、电弧电压和主轴转角。根据实验条件,以下仅分析单相短路情况,并认为短路电流作用在中相触头系统。......
2023-06-15

图10-2 雷诺实验装置雷诺实验发现,流体的流动状态主要是由雷诺数Re的大小决定。如果流体的雷诺数在 2 300~13 800,此时流体的流动称为转换流或过渡流,其流体的流动形态可能是层流也可能是湍流。在此Rec下和Rec上分别表示流体的下临界雷诺数和上临界雷诺数。......
2023-06-29

生活中经历心流越多的人,幸福感越强,心流可以说是衡量幸福的试金石。心流只发生在对个人而言很有挑战性、很有价值的任务时,所以学习、工作更容易产生心流,而运动则最易产生心流。虽然心流极美,被公认为是最佳的幸福体验,但却无法形容,因为太美了。处在心流体验中时,人们只会专注于活动本身,心流过去后,才意识到经历了无比愉悦的时光。......
2023-10-16
相关推荐