第 10 章已经探讨了黏性流体的内部流动,也就是管流问题。本章将讨论黏性流体流经物体外部表面的问题,也就是黏性流体的外部流动。对于有些问题的研究,使用非黏性流体假设可以简化研究过程,又不会影响问题的基本结论,但是在许多实际应用中,流体与接触物体表面不可能不产生黏性作用,使用非黏性流体的假设不仅影响工程计算的精度,甚至获得的结果还会和物体实际运动产生的物理现象相互矛盾,例如达朗贝尔悖论就是一个例子。......
2023-06-29

10.4.1 动能修正系数

10.4.2 管流能量损失
实际流体在管道内的流动过程中因为流体的黏滞效应或流经障碍造成机械能的损失称为管流能量损失,其形成的机理和计算方法各有不同,为了便于分析,常将能量损失分为沿程阻力损失和局部阻力损失两类。
1.沿程阻力损失
所谓沿程阻力损失(Drag loss along the way)是指流体在管道中流动因为流体在管壁之间有黏附作用以及流体质点与流体质点之间存在内摩擦力等因素造成的机械能损失,又称为流体黏性损失(Fluid viscosity loss)或沿程损失(Loss along the way)。而单位重力流体的沿程能量损失则称为沿程水头损失(Head loss along the way)或摩擦损耗落差(Friction loss drop)。理论分析和实验都已证明,沿程水头损失hf与管道长度L和速度的平方 2V成正比,而与管径D成反比,其计算公式为![]() 称为达西(Darcy)公式。式中,f为沿程阻力系数(Drag coefficient along the way)或者是摩擦损耗落差系数(Friction loss drop factor),g为重力加速度。研究发现,摩擦损耗落差系数f与流动状态和管壁的表面粗糙度等因素有关,在圆管内流动的问题中,对于层流流动
称为达西(Darcy)公式。式中,f为沿程阻力系数(Drag coefficient along the way)或者是摩擦损耗落差系数(Friction loss drop factor),g为重力加速度。研究发现,摩擦损耗落差系数f与流动状态和管壁的表面粗糙度等因素有关,在圆管内流动的问题中,对于层流流动![]() 至于湍流流动则必须使用半经验公式配合实验来确定。
至于湍流流动则必须使用半经验公式配合实验来确定。
2.局部阻力损失
所谓局部阻力损失(Local drag loss)是指流体在管道中流动,管道截面面积发生变化或者流经变径管、弯管、三通管与阀门等各种局部障碍装置时,由于管路本身弯曲、变形或者不同形状配件或管路引起的局部机械能损失,流体的局部阻力损失又称为形状阻力损失(Shape drag loss)。而单位重力流体的局部阻力损失则称为局部水头损失(Head loss along the way)或形状损耗落差(Shape loss drop),其计算公式为 式中,hζ为局部水头损失(Local head loss)或形状损耗落差(Shape loss drop);ζ为局部阻力系数(Local drag coefficient)或形状损耗落差系数(Shape loss drop factor),它的大小与流体的雷诺数Re和局部障碍的结构形式有关;V为流体流经管道截面的平均流速,通常是指流体流经局部障碍之后的流速;g为重力加速度,其值为9.81 m/s2。
式中,hζ为局部水头损失(Local head loss)或形状损耗落差(Shape loss drop);ζ为局部阻力系数(Local drag coefficient)或形状损耗落差系数(Shape loss drop factor),它的大小与流体的雷诺数Re和局部障碍的结构形式有关;V为流体流经管道截面的平均流速,通常是指流体流经局部障碍之后的流速;g为重力加速度,其值为9.81 m/s2。
虽然沿程阻力损失和局部阻力损失这两种阻力损失的外因有所差别,但是内因却是相同的,也就是实际流体本身有黏滞性,流体质点之间产生相对运动,一定会产生黏滞切应力,流动阻力引起水头损失,边界的影响只是区分沿程损失和局部损失的依据。通过以上分析可以推知,流体在流动过程中产生阻力损失的两个必要条件为① 流体流动具有黏滞性;② 由于固体边界的影响。
【例10-6】
对于低速流体在管道的流动可能导致流动能量损失的因素是什么?
【解答】
低速流体在管道流动时产生的能量损失,大致可以分成沿程阻力损失和局部阻力损失两类,造成流动能量损失的因素大抵包括流体的黏滞效应以及管道截面面积发生变化或流体流经局部障碍装置产生的机械能损失等几种因素。
【例10-7】
在某制冷系统中,使用管路内径为 d= 10 mm ,管路长度为l=3 m的输油管输送润滑油,已知该润滑油的运动黏度为ν=1.802×10- 4 m2/s ,求体流量 Q= 75 cm3/s 时,输油管的流速、流动状态与沿程水头损失是多少?
【解答】


【例10-8】
如图10-4所示,用长度l=15 m、直径 d= 12 mm 的低碳钢圆管排出油箱中的油。已知油面比管道出口高h=2 m、油的密度 ρ= 815.8 kg/m3、黏度μ=0.01 Pa·s以及管道出口的流动状态为层流(动能修正系数α=2.0),试求油在管道出口处的流速V与流量Q是多少?
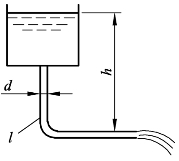
图10-4 圆管排油流动
【解答】

有关工程流体力学基础的文章

第 10 章已经探讨了黏性流体的内部流动,也就是管流问题。本章将讨论黏性流体流经物体外部表面的问题,也就是黏性流体的外部流动。对于有些问题的研究,使用非黏性流体假设可以简化研究过程,又不会影响问题的基本结论,但是在许多实际应用中,流体与接触物体表面不可能不产生黏性作用,使用非黏性流体的假设不仅影响工程计算的精度,甚至获得的结果还会和物体实际运动产生的物理现象相互矛盾,例如达朗贝尔悖论就是一个例子。......
2023-06-29

图10-2 雷诺实验装置雷诺实验发现,流体的流动状态主要是由雷诺数Re的大小决定。如果流体的雷诺数在 2 300~13 800,此时流体的流动称为转换流或过渡流,其流体的流动形态可能是层流也可能是湍流。在此Rec下和Rec上分别表示流体的下临界雷诺数和上临界雷诺数。......
2023-06-29

泡沫质量是指在一定的温度和压力下,泡沫流体中的气体体积与泡沫体积之比,也称为泡沫干度或泡沫特征值。泡沫是一种不稳定流体,当泡沫静止不动时,小泡沫会有向大气泡中扩散的倾向,小气泡变成大气泡后,大气泡就会因为浮力的作用逐渐上升。因此泡沫是一种复杂的流体,它的性能会受到很多可变因素的影响。......
2023-11-18

在工程领域中,静止液体对平面壁面产生影响的研究重点多放在总压力作用力的计算与作用点位置的判定上。试求作用在闸门上的力。由于作用在曲面上各点的流体静压产生的作用力都垂直于容器壁,这就形成了复杂的空间力系问题。......
2023-06-29

研究低速流体力学问题的计算公式主要为流率守恒公式与伯努利方程式这两个,研究的重点放在流动流体流速和压力的变化上。对于低速流动,使用伯努利方程式研究流体流动时压力与速度的变化,其计算结果与实际测量结果之间的误差其实不大,以致于可以将误差忽略不计。......
2023-06-29

通常在研究流体力学问题时,主要是研究流体在静止或运动时流场的性质或运动参数的变化以及流体运动的基本规律。一般而言,研究流体力学问题的方法大概可以分成理论解析法、实验观测法以及数值计算法。其优点在于研究费用较少,可以计算复杂的流体流动问题,计算结果也与真实现象之间的偏差较小。......
2023-06-29

图10-5 不可压缩流体在圆管内做均匀层流运动10.5.2 流体流场的速度分布情形圆管层流的最大速度umax为于r=0处,其计算公式为。......
2023-06-29

正常条件下,一般黏性土的抗渗强度取决于粒团遇水后的稳固程度。粒团遇水后的稳固程度主要决定于黏土矿物成分,黏土矿物以伊里石居首位;含有高岭石和蒙脱石的黏性土,颗粒组成中黏粒含量多在30%以下,粉粒居多,塑性指数多小于22%,多属低限液限黏土。式即为黏性土抗渗强度,在不考虑黏聚力的抗渗作用下,流土型黏性土的抗渗强度与砂性土完全一致。......
2023-06-28
相关推荐