黏性流体运动的两种形态详解

2023-06-29 理论教育版权反馈

【摘要】：图10-2 雷诺实验装置雷诺实验发现，流体的流动状态主要是由雷诺数Re的大小决定。如果流体的雷诺数在 2 300～13 800，此时流体的流动称为转换流或过渡流，其流体的流动形态可能是层流也可能是湍流。在此Rec下和Rec上分别表示流体的下临界雷诺数和上临界雷诺数。

英国物理学家雷诺在 1883年发表了他的实验结果。他通过大量的实验研究发现，实际流体在管路中存在两种不同的状态，并且确定了层流和湍流这两种流动状态转换的必要条件，其实验装置如图10-2所示。

pagenumber_ebook=220,pagenumber_book=213

图10-2 雷诺实验装置

雷诺实验发现，流体的流动状态主要是由雷诺数Re的大小决定。在流体的流动速度很慢的情况下，流体的雷诺数很小，有色液体成一条直线平稳地流过整根玻璃管而与管内的水不相混合，此时玻璃管流体的流动形态称为层流，其流动状态如图10-3（a）所示。随着调整控制阀逐渐增大，水流速度加快，从而雷诺数增加，当流体的雷诺数增大到一定数值时，有色液体流经玻璃管的流线会出现不规则的波浪形，此时流体的流动称为转换流或过渡流（Transition flow），其流动状态如图10-3（b）所示。此时如果继续增大流速使流体雷诺数增加，当流体的雷诺数达到某临界值时，整个玻璃管内的水呈现均匀的颜色，这说明流体质点除了沿管道向前运动外，还存在不规则的径向运动，质点间相互碰撞相互混杂，此时流体的流动称为湍流或紊流，其流动状态如图10-3（c）所示。

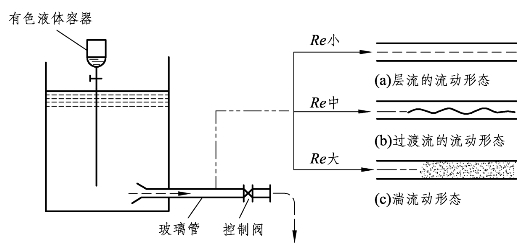
pagenumber_ebook=220,pagenumber_book=213

图10-3 层流、过渡流与湍流的流动形态示意图

雷诺发现，对于一般的管流，如果流体的雷诺数低于 2 300，流体的流动形态为层流。此临界的雷诺数Re称为下临界雷诺数（Lower critical Reynolds number），用符号Rce下表示。如果流体的雷诺数Re高于 13 800，流体的流动形态为湍流，此临界的雷诺数Re称为上临界雷诺数（Upper critical Reynolds number），用符号Rec上表示。如果流体的雷诺数在 2 300～13 800，此时流体的流动称为转换流或过渡流，其流体的流动形态可能是层流也可能是湍流。过渡流的状态极不稳定，只要外界稍有扰动，就有可能会转变为湍流，因此一般将过渡流归属为湍流问题处理。而以Re下≈2 300作为判别层流与湍流的标准，因此工程业界常说的临界雷诺数指的是下临界雷诺数，而对于圆形管流而言，如果流体的雷诺数低于 2 300则可以直接将管内流体的流动形态判定为层流。必须注意的是临界雷诺数并不是一个准确的固定常数，它随管壁的表面粗糙度、圆形管入口处水流的扰动大小等实验条件不同而有所变化。如果入口处水流的扰动大，则临界雷诺数就低；如果入口处水流的扰动小，则临界雷诺数就高。利用这一现象可以用人为的方式产生一些扰动以促使湍流的发生，产生这类扰动的装置称为激流装置。雷诺实验得出的圆管流动下临界雷诺数为 2 300，但有些教科书采用的临界雷诺数是2 000或2 320。这也是临界雷诺数与干扰有关的缘故，雷诺的实验环境受到的干扰极小，实验前水箱中的水体经长时间的稳定作用，经反复多次细心测量才得出的，而后人的大量实验很难重复得出雷诺实验的准确数值，通常为 2 000～2 300。从工程实际出发，圆管临界雷诺数一般取在2 300左右。

【例10-2】

层流流场、湍流流场以及过渡流的判定准则是什么？

【解答】

雷诺在实验的过程中发现，流体流场的流动状态主要是由雷诺数Re的大小决定，如果0 ＜ Re ＜ Rec下，则流体流场的状态为层流流场；如果 Rec下＜ Re ＜Rec上，则流体流场的状态为过渡流场；如果 Re＞Rec上，则流体流场的状态为湍流流场。在此Rec下和Rec上分别表示流体的下临界雷诺数和上临界雷诺数。

【例10-3】

临界雷诺数（Critical Reynolds number）的定义是什么？

【解答】

流体流场的状态开始由层流转变成湍流时的雷诺数称为临界雷诺数Rce，也就是一般常用的流场状态判定准则中下临界雷诺数（Lower critical Reynolds number）。

黏性流体运动的两种形态详解

相关推荐