因次分析法：物理量因次乘幂分析和无因次参数组合研究

2023-06-29 理论教育版权反馈

【摘要】：9.3.3 因次分析法的目的与研究方法因次分析法是从因次齐次性定理为出发点，针对与研究问题有关的物理量做因次乘幂分析，并进一步将它们转换成无因次参数的组合，从而统一研究各个物理量在因次上的内在联系。

从事工程设计和科学研究的过程中，常常会遇到根据经验分析判断研究的问题是否与某些物理量有关，运用既有理论方法一般无法准确地描述这些物理参数对研究问题的影响，此时，必须使用实验的方式寻求物理现象的规律。但是对情况复杂的工程问题，如果单个与逐次改变每一个物理参数去做实验，不仅耗费时间，也无法完整地找出这些物理参数的关联性、规律性与通用性。长期的科学实验研究发现可以利用因次分析法（Dimensional analysis method）解决此一难题。

9.3.1 因次的概念

在工程研究中，所谓单位是用来描述物理量大小的计量尺度，而因次则是用来表示物理量单位的属性，因次的概念是研究因次分析法的基础。

1．因次的定义

工程设计和科学研究的过程会涉及各种物理量，例如质量、时间、力、速度、长度等都是研究问题时常遇到的物理量。这些物理量都是具有单位（Unit）的，物理量单位属性的表示即称为因次或量纲（Dimension）。同一物理量可以用不同的单位来度量，但只有唯一的因次，例如，时间可以 h、min、s 等不同单位来度量，但是作为物理量的属性，都属于时间因次，用符号 T 来表示。长度可以用 m、cm、ft、in 等不同单位来度量，但作为物理量的属性，都属于长度因次，用符号L来表示，质量可以用kg、g、slug等不同单位来度量，但作为物理量的属性，都属于质量因次，用符号 M 来表示。工程上物理量的因次用符号dim表示，例如密度的因次表示为 dimρ= ML-3。

2．因次的类型与表示

如果能够适当地规定某些固定物理量当作基本的物理量，并使用其因次符号表示，而将其他物理量表示成由这些基本物理量的因次符号组成的乘幂形式，就可以统一研究各个物理量之间的关系，这就是因次表示法的概念。在因次表示法中，这些被指定基本物理量的因次，称为基本因次（Primary dimension），而由基本因次衍生的因次就称为导出因次（Secondary dimension）或衍生因次（Derivative dimension）。

3．基本因次的定义

单位可以分成公制单位与英制单位，因次的划分也是如此。公制单位制常用的基本因次符号是M、L、T与Θ，对于英制单位制常用的基本因次符号是F、L、T与Θ，其中M为质量的因次代表符号，L为长度的因次代表符号，T为时间的因次代表符号，Θ为温度的因次代表符号以及F为力量的因次代表符号。也就是说，在研究流体流动问题的过程中，公制单位制与英制单位制选用的基本因次不完全相同。对于公制单位选用为基本因次的物理量是质量、长度、时间与温度，而对于英制单位制选用为基本因次的物理量是力量、长度、时间与温度。由于公制单位制与英制单位制选用的基本因次不同，虽然两种单位制在求取导出因次与无因次参数时的观念与方法相同，但是两者求得的导出因次与无因次参数的形式有所不同。本书主要选用的单位是公制（标准制）单位，选用的基本因次为质量 M、长度L、时间T与温度Θ四个基本因次。一般而言，除了研究有关燃烧或化学的问题，通常都不考虑温度Θ这个基本因次。

4．导出因次的定义

当选定了基本因次的项目，所有的物理量都可以用基本因次的乘幂形式来表现，这些由基本因次衍生的因次就称为导出因次，例如对于公制单位制，选用的基本因次是质量、长度、时间与温度，因为速度是长度/时间，所以其因次（导出因次）为 LT-1。

5．常用的物理量因次表

要学好因次分析法，不仅需要掌握基本因次与导出因次的概念，还必须熟记常用物理量的因次，如表9-1所示。

表9-1 常用物理量的公制单位制因次表

pagenumber_ebook=213,pagenumber_book=206

9.3.2 因次齐次性定理

所谓因次齐次性定理（Dimensional homogeneity theorem）是指凡是能够描述物理现象的方程式，其在方程式中的各项之因次都必须是齐次的，也就是说方程式中的每一项的因次都必须相同，例如伯努利方程式，式中P项的因次为项的因次为ML- 3 × LT -1 × LT -1=ML-1 T -2，而 Pt项的因次也是 ML-1T -2。研究证明凡是能够描述某一个物理现象的方程式都必须满足因次的齐次性，所以因次的齐次性被当作初步判定物理方程式是否正确的准则。

9.3.3 因次分析法的目的与研究方法

因次分析法是从因次齐次性定理为出发点，针对与研究问题有关的物理量做因次乘幂分析，并进一步将它们转换成无因次参数的组合，从而统一研究各个物理量在因次上的内在联系。此研究方法可以在降低问题研究影响变量数量的情况下，完整地找出这些物理参数的关联性、规律性与通用性。在流体力学的研究中，因次分析法是与相似理论关系密切的另一种通过实验探索流体流动规律的重要方法，它和相似理论在流体力学中并称为指导实验研究的两大基础理论。

1．因次分析法的使用目的

因次分析法是将影响问题研究的物理参数转换成无因次参数的组合，在降低问题研究难度与研究参数数量的情况下，找出影响物理参数的关联性与流动现象的通用性。因次分析法具有许多好处，描述如下。

（1）节省研究成本。因次分析法可以将问题研究的物理参数转换成无因次参数的组合，使得研究参数的数量减少，在问题研究时可以节省大量的时间、人力和财力，达到节省研究成本的目的。

（2）有利实验与理论的结合。使用因次分析法整理获得的研究结果可以直接用于模型实验或理论分析上，有利于实验与理论的结合。

（3）有助于工业应用与科学研究的发展。使用因次分析法可以针对每个无因次参数加以讨论，从而找出无因次参数相对应的流体流动或空气动力特性，获得通用性的运动规律。使用因次分析法获得的研究结果可以应用于原型及其他相似的流动，不需再针对相同类型的流体流动进行研究，有助于工业应用与科学研究的发展。

2．常用的无因次参数

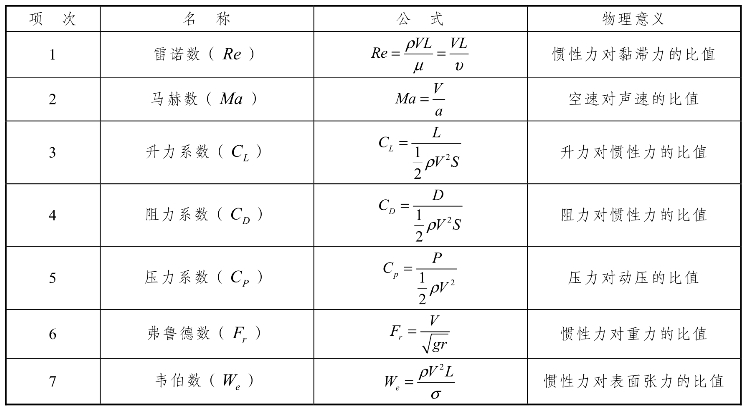
因次分析法的第一步将问题研究的物理参数转换成无因次参数的组合，所以在研究流体力学时，如果熟悉常用的无因次参数及其代表的物理意义，将有助于因次分析法的学习，常用无因次参数及其代表的物理意义如表9-2所示。

表9-2 常用的无因次参数表

pagenumber_ebook=214,pagenumber_book=207

3．因次分析法的研究方法与步骤

一般使用π定理，又称白金汉（E Buckingham）定理，它是指如果一个流动现象涉及n个物理量与j个基本因次，则这个现象可以用n-j个无因次参数来描述，而且这些无因次参数之间的函数关系为 πi=f (π1，π2，… ，πn-j)，例如使用π定理得到的无因次参数为 π1、 π2与π3，则 π1、 π2与 π3之间的函数关系可以表示为 π1=f (π1，π3)。通常使用π定理研究流动现象可以将其分解成六个步骤进行，就能获得影响现象的无因次参数与这些参数之间的关联性，从而找出流体流动的特性。

（1）找出影响变量（物理量）的个数n。使用因次分析法（π定理）的第一个步骤是找出所有与流体流动现象有关的物理量，这是非常重要的步骤，因为只要缺少任何一个，就会得到不全面的，甚至是错误的结果。

（2）列出每个物理量的因次。在找出与流体流动现象有关的全部物理量后，必须将物理量表示成以基本因次为基础的乘幂形式，也就是如果为基本因次的物理量，以基本因次表示，如果物理量不选定为基本因次，以导出因次来表示。例如在公制单位选用的基本因次物理量是质量、长度、时间与温度，于是质量的因次是基本因次M，而压力为导出因次 ML-1T-2。

（3）找出无法形成“无因次参数π”的个数j。通常j值为所列物理量中所有不同基本因次的数目，标准单位在探讨流体力学问题的过程中选用的基本因次为M、L T、与Θ，一般除了研究有关燃烧或化学的问题多不讨论Θ这个基本因次。所以在研究流体力学时，j值多为3或更少，也就是j≤3。

（4）找出“无因次参数π”的个数k。从前面的内容可知n、j与k之间的关系必定满足n-j=k的关系式。

（5）利用乘幂法找出无因次参数π。将j+1个物理量的因次指数相乘并设法让乘积中基本因次的乘幂指数都等于0，即求得无因次参数。

（6）将无因次参数表示为与其他无因次参数的函数。也就是将这些无因次参数之间的函数关系表示为 πi=f(π1，π2，… ，πn-j)的关系式。

4．数据的创新及使用

一般而言，使用的无因次参数配合相似准则的概念有效地将理论与实验研究结合，并且能够作为两者研究得到的数据与实体运动数据相互转换的桥梁，但是有时常使用无因次参数，例如雷诺数Re、马赫数Ma、弗鲁德数Fr、升力系数CL与阻力系数CD等并不能明确地指出需研究探讨物理现象，此时就必须再次地利用因次分析法去重组无因次参数，直到能够明确地表示所需研究探讨的物理现象为止。

【例9-2】

已知密度为ρ不可压缩流体，以均匀流速U0及迎角α流经弦长为C与弦宽为b的薄平板（假设为二维流场），用因次分析法求出该平板的升力L与上述 ρ、U0、 α、b 与C等参数间的无因次关系式。

【解答】

使用π定理研究流体流动现象的六个步骤进行求解。

（1）找出影响变量（物理量）的个数n。由题干可知问题的影响参数为升力L、密度ρ、速度U0、迎角α及面积S（此S为平板的上视面积，也就是S=bc），所以n=5。

（2）列出每个物理量的因次。参考如表 9-1 所示常用物理量的公制单位因次表，每个物理量的因次详列如下。

① 升力L的因次为 MLT-2。

② 密度ρ的因次为 ML-3。

③ 速度U0的因次为 LT-1。

④ 面积S的因次为 L2。

⑤ 迎角α则为无因次参数。

（3）找出无法形成“无因次参数π”的个数j：从步骤（2）可知，问题中的基本因次为质量M、长度L以及时间T三个基本因次，所以j=3。