相似理论在飞机设计中的应用：风洞测试

相似理论是指导模型实验设计，获得与实物原型相同运动规律的重要理论。在流体力学的研究中，所谓原型是指在流体流场内实际运动的实物，而实验模型则是指在实验中根据原型（实物）按照一定比例关系缩小（或放大）做出的代表物。由于流体流动的现象非常复杂，工程实践与科学研究的过程经常需要依靠实验寻求物理现象的规律或者验证理论解析和数值计算的结果。对于尺寸较大的实物（例如车辆、船舶与飞机等），由于结构复杂与造价昂贵，通常先在缩小的模型上进行实验，得到所需的实验结果后，再换算到实物上去。然而想得到模型实验与实物运动同样的规律，就必须使实验模型与实物原型符合相似理论，因此相似理论被认为指导模型实验研究的理论基础，在流体力学的研究中占有非常重要的地位。

9.2.1 相似理论的目的

相似理论的主要目的是建立实验模型与实物（实体原型）的关联性，人们在经过长期的科学实验，终于探索和总结出一个结论，就是如果实验模型（Model）与实体原型（Protype）之间的关系符合相似法则（Similarity rule），也就是实验模型与要设计或研究的实物（实体原型）之间满足几何相似、运动相似以及动力相似等条件，利用实验模型观察到的流体物理特性就会与实物运动具有同样的流动规律。这一经验理论即称为相似理论（Similitude theory）。由其定义可知，研究实验模型与实物运动彼此之间流动相似现象的理论即称为相似理论，它将实验结果换算到实物运动并找出其流体流动规律性。相似理论的发现，使得大量的研发时间、人力与金钱得以节省，并避免了许多研发时的危险与风险，因此视为指导模型实验研究时的主要基础理论。

9.2.2 几何相似的意义

几何相似关心的是长度因次{L}，在任何敏感的模型测试实验中，实验模型与实体原型（实物）之间的几何相似都是首先必须满足的条件。其定义描述为“如果实验模型和实体原型（实物）两者在三个坐标轴上所有的对应尺寸都呈现相同线性比例，则称此两者之间满足几何相似的关系”，当然从严格意义来说，实验模型和实体原型（实物）之间要满足几何相似的条件，不仅两者之间对应的长度比例必须保持不变，而且两者对应的角度与流体流经两者的流动方向也必须完全一致对应。甚至从更严格的角度来看，实验模型与实体原型（实物）两者之间的表面粗糙度也应该具有相同的线性比例。但是实际上，这是不可能完全做到的，在模型实验设计中只能尽可能地近似，实验的结果会和实际的情况有误差，只要其误差在容许范围内即可接受。

9.2.3 运动相似的意义

所谓运动相似（Kinematic similarity）是指实验模型和实体原型（实物）两者之间具有相同的对应长度比例与对应时间比例，也就是两者之间具备相同的对应速度比例。要让模型实验设计满足运动相似条件，除了必须让实验模型和实体原型（实物）之间满足几何相似，还必须使模型和原型两者之间对应的速度方向完全相同以及速度大小呈现一定比例关系。

9.2.4 动力相似的意义

所谓动力相似（Dynamic similarity）是指实验模型和实体原型（实物）两者之间具有相同的对应比例。在从事模型实验设计时，如果要使实验模型和实体原型（实物）两者之间满足动力相似条件，几何相似是首先必须满足的条件。除此之外，还必须具备相同的力量比例及压力系数CP，从严格意义来看，要使模型实验设计满足动力相似条件，实验模型和实体原型（实物）两者之间的所有无因次参数都必须对应相同，但是由于实际流动非常复杂，所有类型的力量都满足相同的对应比例是不可能的。长期的科学实验发现，在观察流体的流动特性时，通常只有一到两种类型的作用力起着主要作用，因此，在进行流体流动的实验研究时，通常是在满足几何相似条件前提下，要求实验模型和实物原型两者之间只需满足主要作用力的动力相似即可，对流动现象不起主要作用的其他力则忽略不计。

9.2.5 流动相似的意义

在模型实验设计中，几何相似是必须满足的首要条件，如果不满足实验模型和实体原型（实物）等比例缩小的原则，模型实验也就失去了实质意义。要使得流体在实验模型上的流动能够表现出在实体原型（实物）上流动时的主要现象和特性，并从流体在实验模型上的流动情形预测出在实体原型（实物）上流动的结果，就必须使流经模型流动与原型流动保持几何相似、运动相似以及动力相似的关系。在流体力学中，当模型流动与原型流动两者之间满足几何相似、运动相似以及动力相似条件，则称两者为流动相似（Flow similarity）。工程的实践经验发现，当模型流动与原型流动两者之间为流动相似，模型实验中观测到的物理现象会与实物运动具有同样的规律，这也就是相似理论所要表达的主要物理意义。简单地说，当模型流动和原型流动两者之间呈现流动相似的关系时，模型实验观察到的流动现象与规律与实物运动的情形相同，因此可以从流体在实验模型上的流动情形预测出流体在实物原型上流动时的结果，这也就是流体力学中模型实验的原理。

9.2.6 风洞测试

风洞（Wind tunnel）是一种飞机设计过程中以相似理论为基础建立的一种使用实验模型来仿真实体运动，从而找出实物运动规律的研究装置，它可以节省时间、人力与成本，并且避免直接进行实体测试时可能遭遇到的意外与风险，在飞机及车辆的设计和研发过程中广泛应用。

1．功用与构造

如图9-2所示，风洞测量利用模型仿真飞机在运动时的空气动力特性，目的在于节省飞机在设计过程中的人力、物力和财力的浪费。

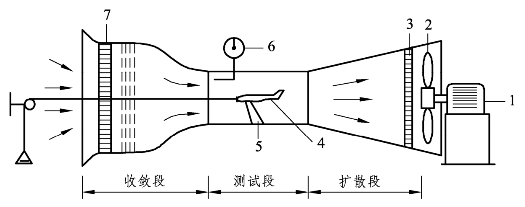
图9-2 低速风洞实验的示意图

1—电动机；2—风扇；3—防护网；4—飞机模型；5—支架；6—空速表；7—整流格。

2．吹试条件

要利用风洞来研究实体飞机飞行的空气动力特性，飞机模型和真实飞机实体之间必须满足几何相似以及马赫数相同和雷诺数相同等条件。

3．Prandtl-Glauert规则

高速风洞较低速风洞价格昂贵且在实验时易发生危险，往往按照 Prandtl-Glauert 规则将低速风洞测量的空气动力数据模拟高速飞机飞行的空气动力特性。

（1）目的。Prandtl-Glauert规则的目的是建立可压缩流与不可压缩流中相同翼型的气动力参数的关系，进而得到可压缩性对同一翼型的影响。

（2）公式为式中，CP,可压为可压缩流中机翼翼型表面的压力系数，CP，不可压为不可压缩流中机翼翼型表面的压力系数，Ma为飞行马赫数。

【例9-1】

在亚声速风洞实验中，当风速 U0=30 m/s 时（经计算 Ma∞= 0.088），在模型翼型上某个测试点的压力系数 CPi=-1 .18，当风速增加到 U0=204 m/s ，相应条件相同情况下，问其马赫数增加到多少？并利用Prandtl-Glauert规则求出该点压力系数CPi。

【解答】

（1）当 Ma∞= 0.088时，因为马赫数非常小，能够确定在模型翼型上的空气流动都为不可压。

（2）根据马赫数的计算公式由题干可知声速值当风速增到 U0=204 m/s 时，。

9.2.7 模型实验与相似理论的适用时机

在工程实践与科学研究的过程中，经常需要依靠模型实验探求实物运动表现出的物理现象、运动规律以及验证理论与数值计算结果，例如本章前面介绍的“风洞测试”即属一例。在流体力学的研究中，所谓模型实验是指依据相似原理把实物原型按一定比例缩小制成模型，并且利用简化的控制方法找出或重现实际发生的物理现象的一种方法，在工程实践上，许多科学研究和生产设计的研发过程都必须做模型实验。相似理论虽然可以指导模型实验设计并建构起模型实验与实物运动之间研究数据相互转换的桥梁，但在工程实际执行上，模型实验不可能都满足所有的动力相似条件，必须掌握研究的方向与重点，才能找出实际流动现象的物理本质。如果不能够确认研究的重点，也不能保证实验模型和实物原型中流动现象之间的物理本质相同，进行模型实验是没有价值的。并不是所有的流动现象都能做到进行模型实验，只有对其流动现象有足够的认知并了解支配其现象的主要物理法则，在不适合对其做理论分析或数值模拟的原型时才适合利用相似理论建构模型实验来研究相关流动现象。进行模型实验研究流体流动规律时，必须以满足几何相似条件为前提，再根据实际要求实验模型和实体原型（实物）两者之间满足运动相似以及影响问题研究主要作用力的动力相似，才能在最佳能效的情况下找到研究的流体流动或者实际物体运动的物理现象与规律。

9.2.8 常见的相似准则

虽然相似理论可以建构模型实验与实物运动之间研究数据相互转换的桥梁，但是进行模型实验时不可能都满足所有的动力相似条件，如何让模型实验有效地掌握研究的重点一直是流体力学研究讨论的课题。经过长期科学实验与研究后发现使用相似准则的概念可以有效地改善或解决此难题。

1．相似准则的概念

所谓相似准则（Similarity criterion）是用来判断两个流动现象之间相似性使用的无因次参数。工程实践中发现，彼此相似的流动现象必定具有数值相同的相似准则，而如果相似准则的数值相同，其对应的流动现象必定相似。在流体力学的研究中，相似准则的概念一直是模型实验、理论计算与分析以及实体运动之间研究数据彼此验证的基础。一般而言，如果模型实验、理论计算与分析以及实体运动在彼此之间满足相似准则，其彼此对应的流动现象和流动规律必定相似。在流体力学工程中，常使用的相似准则包括雷诺数相似准则、马赫数相似准则、弗鲁德数相似准则、韦伯数相似准则和欧拉数相似准则等。

2．雷诺数相似准则

雷诺数相似准则以其用来判定的准则为雷诺数（Reynolds number）Re而命名，从物理观点来看，流体的雷诺数Re可视为流体流场惯性力与黏滞力的比值，而从数学的定义来看流体的雷诺数可以用表示，式中，ρ为流体的密度，V为流体流动的速度，L为特征（参考）长度，μ为流体的动力黏度。雷诺数相似准则主要用于以流体黏性力为主要作用力的两个流动现象是否满足动力相似的判定依据，所以又称为黏性力相似准则，它是流体力学研究中最重要的相似准则。当两个流动现象之间满足黏性力相似条件时，此两者的雷诺数Re必定相等，反之亦然，这就是雷诺数相似准则的主要意义。

3．马赫数相似准则

马赫数相似准则以其用来判定的准则为马赫数（Mach number）Ma而命名，从物理观点看来，流体的马赫数Ma可以视为流体的流速V对声速a的比值，其数学定义为马赫数相似准则主要用于以流体弹性力为主要作用力的两个流动现象是否满足动力相似的判定依据，所以又称为弹性力相似准则。气体的体积弹性系数与气体的压缩性有关，所以如果两个流动现象之间满足压缩性相似条件，此两者的马赫数Ma必定相等，反之亦然，这就是马赫数相似准则的主要意义。

4．弗鲁德数相似准则

弗鲁德数相似准则以其用来判定的准则为弗鲁德数（Froude number）Fr而命名，从物理观点看来，流体的弗鲁德数Fr可以视为流体的惯性力对重力的比值，从数学定义来看，流体的弗鲁德数Fr可以用公式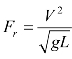计算得到，式中，V、g与L分别为流体的流速、重力加速度以及特征（参考）长度。弗鲁德数相似准则主要用于以流体的重力为主要作用力的两个流动现象是否满足动力相似的判定依据，所以又称为重力相似准则。当两个流动现象之间满足重力相似条件时，此两者的弗鲁德数Fr必定相等，反之亦然，这就是弗鲁德数相似准则的主要意义。

5．韦伯数相似准则

韦伯数相似准则以其用来判定的准则为韦伯数（Weber number）We而命名，从物理观点看来，流体的韦伯数We可以视为惯性力对表面张力的比值。从数学定义来看，流体的韦伯数We可以用公式来计算，式中，ρ 、V 、L 与σ分别为流体的密度、流速、特征（参考）长度以及表面张力系数。韦伯数We主要用于以流体的表面张力为主要作用力的两个流动现象是否满足动力相似的判定依据，所以又称为表面张力相似准则。当两个流动现象之间满足表面张力相似条件时，此两者的韦伯数We必定相等，反之亦然，这就是韦伯数相似准则的主要意义。

6．欧拉数相似准则

欧拉数相似准则以其用来判定的准则为欧拉数（Euler number）Eu而命名，从物理观点看来，流体的欧拉数Eu可以视为压力对惯性力的比值。从数学定义来看，流体的欧拉数Eu可以用公式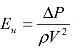计算，式中，P、 ρ 与V分别为流体的压力、密度和流速。欧拉数相似准则主要用于以流体的压力为主要作用力的两个流动现象是否满足动力相似的判定依据，所以又称为压力相似准则。当两个流动现象的雷诺数相等，欧拉数也通常会相等；而弗鲁德数相等，欧拉数也通常会相等。所以只有液体出现负压或存在空蚀现象，欧拉数相似准则（两个流动现象的欧拉数相等）才可用来保证液体在流动时满足动力相似。

7．综合讨论

理论上，模型实验应同时满足上述各项相似准则，也就是要求流体流经实验模型与实物原型的雷诺数Re、马赫数Ma、弗鲁德数Fr、韦伯数We以及欧拉数Eu都必须对应相等，但是在工程实践中很难做到所有的相似准则条件都完全满足。因此，在进行模型实验研究流体的流动规律时，满足几何相似条件为前提，然后根据实际的研究要求实验模型和实物原型满足影响问题研究主要作用力的相似准则条件。

（1）可压缩流体流动的模型实验。一般而言，对于可压缩流体流动的模型实验，模型和原型的雷诺数Re以及马赫数Ma必须对应相等，也就是必须满足雷诺数相似准则以及马赫数相似准则这两个相似准则条件。

（2）有自由液面的不可压缩流模型实验。对于自由液面并且允许液面上下自由变动的各种液体流动，例如堰坝溢流、孔口出流、明槽流动以及隧洞流动等重力起主要作用的液体流动，模型和原型的雷诺数Re、弗鲁德数Fr以及韦伯数We必须对应相等，也就是必须满足雷诺数相似准则、弗鲁德数相似准则以及韦伯数相似准则这三个相似准则条件，如有必要，欧拉数Eu也必须对应相等。

（3）无自由液面的不可压缩流模型实验。对于深水下的潜体运动以及管道中的流动通常遵循雷诺数相似准则，也就是以模型和原型的雷诺数Re对应相等来保证液体在流动时满足动力相似。

通常依此标准去设计模型实验，所得的结果应该是可接受的，也就是可以在最有能效的情况下找到研究的流动或者实际物体运动的物理现象与规律。