第七节矛盾的分类问题对社会主义时期的矛盾进行科学分类是一个重要的理论课题和方法论课题。按照一类二类矛盾的分类法，把敌与我、革命与反革命、无产阶级与资产阶级的矛盾看成是不能结合的，这大概是大家都会同意的。因为一类二类矛盾的分类法也是以承认“两个为主”为其基本理论依据的。在我看来，两个为主的矛盾分类方法值得研究的地方并不比前一种分类方法少，某些方面，要在理论上说得圆通难度也许更大。......
2023-11-28
达朗贝尔悖论：流体黏度与阻力矛盾的问题
【摘要】：但是实验证明，即使黏性很小的流体，它们流过圆柱体或其他物体时，都会产生阻力，所以这个推导的结果与一般人的认知有差异，也与实际测量的结果产生矛盾，称为达朗贝尔悖论。达朗贝尔悖论是使用理想流体的假设与实测结果产生矛盾最有名的例子，其计算结果与实验测量产生差异原因在于不可压缩势流理论将流体的黏度忽略不计，也就是假设流体的黏度μ=0。这就是有名的达朗贝尔悖论。
法国物理学家达朗贝尔在 1752年根据不可压缩势流的迭加运算法则推出了平面理想流体均匀等速通过圆柱体流动，作用在圆柱面上既无升力，也无阻力的结论。但是实验证明，即使黏性很小的流体，它们流过圆柱体或其他物体时，都会产生阻力，所以这个推导的结果与一般人的认知有差异，也与实际测量的结果产生矛盾，称为达朗贝尔悖论。达朗贝尔悖论是使用理想流体的假设与实测结果产生矛盾最有名的例子，其计算结果与实验测量产生差异原因在于不可压缩势流理论将流体的黏度忽略不计，也就是假设流体的黏度μ=0。正因为达朗贝尔悖论，后续流体流动研究并不能用不可压缩势流的迭加运算来求取物体在流体中运动或流体流过物体时产生的阻力解，那是不切实际且不可能的做法。
【例8-15】
已知密度为ρ不可压缩无黏性流体，以均匀流速U0流经一个圆柱体，其流线分布可用流线函数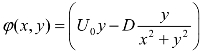
来表示，式中D为偶极流强度。
（1）试求出该流体的速度表达式。
（2）试求出圆柱体横截面的半径a。
（3）该圆柱面上所受的升力L与阻力D各是多少？并请论述造成该计算结果的原因。
【解答】
图8-17 均匀流流经圆柱体
（3）根据伯努利方程，圆球上下对称无压差，所以圆柱所受的升力为 0。一般而言，物体承受的阻力可分为压差阻力（形状阻力）和摩擦阻力两种，因为圆球左右对称对称无压差，所以压差阻力为0。题目假设流体的黏度忽略不计，所以摩擦阻力为0。这就是有名的达朗贝尔悖论。因为任何物体的流动都会产生摩擦阻力，而本题的摩擦阻力为0，所以势流理论不适用于研究流体流动时产生之阻力问题。
有关工程流体力学基础的文章
- 详细阅读
-
低速流体力学问题中的流体假设与实验验证详细阅读
研究低速流体力学问题经常使用的假设主要有稳态一维流动、不可压缩流体、非黏性流体、理想流体、平均流速与流管等。因此采用非黏性流体假设的结果都必须利用实验来检验其精确度与可用性。......
2023-06-29
-
眼镜的悖论：眼镜和生活中的伦理问题详细阅读
看来眼镜到了一定的领域也就是有了一定的意义。眼镜没有配成，所以到了今天我的眼镜前边还是空气，最直接的就是我们生活的这个世界。尽管许多时候生命的本质是用生命的表象来完成体现的，但是生命的个体有时候在许多场合总也是要生出悖论来的。我的妈呀，不就是给儿子配一副眼镜吗，怎么转眼间出现了这么严重的伦理问题。......
2024-01-25
-
研究流体力学问题的方法优化详细阅读
通常在研究流体力学问题时，主要是研究流体在静止或运动时流场的性质或运动参数的变化以及流体运动的基本规律。一般而言，研究流体力学问题的方法大概可以分成理论解析法、实验观测法以及数值计算法。其优点在于研究费用较少，可以计算复杂的流体流动问题，计算结果也与真实现象之间的偏差较小。......
2023-06-29
-
巧妙解矛盾，不积累大问题详细阅读
称呼与身份一定要相符，要注意用关心和体贴的语气和对方交流。当对方讲话时，一定要认真听，如果对方讲个不停，不要表现出不耐烦，更不能随意打断对方的讲话，可以通过发问巧妙地把话题转移。在沟通过程中，与被沟通对象要坦诚相见。只有真正懂得礼节并且有理智的女性才能做到良好沟通，化解矛盾，并且获得周围知情者的赞赏，为自己的人际交往打开更大的局面。......
2023-07-25
-
流体流动问题的分类方法及应用场景详细阅读
1.8.1 稳态流场与非稳态流场由于流体连续性假设的缘故，通常在研究流体力学问题时都会把流体的压力、温度与密度等流体性质以及流体的流速表示位置和时间的函数。......
2023-06-29
-
流体静压的计算原理与应用详细阅读
图2-1 流体静压定义与其作用方向的示意图2.2.2 静压的计算实验表明在静止流场中，液体和气体承受的相对压力，仅与液体或气体的密度和高度有关，而与其他因素无关，这个结论即称为静压理论。根据静压理论计算公式与前面推得 PB=PC的结果，可进一步推得关系式 PB=PA+ρ1ghAB=PC=P0+ρ2ghCD。......
2023-06-29
-
矛盾规律研究：差异与矛盾的争议及条件详细阅读
第六节差异与矛盾差异是不是矛盾，这是一个有争议的问题。一些同志认为，差异就是矛盾这个命题是科学的，符合实际情况；一些同志则认为，并不是一切差异都是矛盾。英国贵族和我国工人的特点有很大的差异，但他们之间并不是矛盾。应该明确，这是矛盾的差别性问题，不是矛盾的有无问题。我们不能说因为张三和李四是有差异的，因而他们就是矛盾。应该说，有差异的事物，只有在一定条件下才可能构成矛盾。......
2023-11-28
相关推荐