根据第 7章以及本章前面内容得到的结果可知,如果流体为平面理想流体,也就是平面不可压缩势流时,流线函数φ和速度势函数Φ两者会同时存在。和均匀等速流类似,源流和汇流也是求解复杂平面理想流体流动时常用的基本平面不可压缩势流流动之一。......
2023-06-29
前面介绍了几种简单的平面不可压缩势流(平面理想流体的流动),重要的不只是它们能代表怎样的实际流动,而在于它们是多数复杂平面不可压缩势流迭加运算中所需的基本组成流动,如果将这几种基本流动组合在一起,就能够形成许多有重要意义的复杂流动,这样就无须耗费巨大的费用去实验,就能模拟流体的流动情况并获得某些流动规律,有利于某些流体现象的初步研究。这里以均匀等速流、源流和汇流以及势涡流基本流动为例,叙述如何利用平面不可压缩势流的迭加运算来获得流体流动规律。
8.4.1 迭加运算的原理
如前所述,平面不可压缩势流在流动时流线函数φ和速度势函数Φ同时存在并满足拉普拉斯方程,也就是φ和Φ是满足∇2φ=0与∇2φ=0的调和函数。拉普拉斯方程是线性齐次方程,方程解具备可以迭加的特性,也就是流线函数或速度势函数的线性组合仍然能够满足拉普拉斯方程,即满足![]() 式中 φ1、 φ2、 φ3、 …、φn和Φ1、Φ2、Φ3、 … 、Φn分别是简单平面不可压缩势流的流线函数与速度势函数解,而φ和Φ分别是流线函数与速度势函数的组合解,因此平面不可压缩势流具有 φ= φ1+φ2+φ3+…+φn和 φ= φ1+φ2+φ3+…+φn的特性,即在平面不可压缩势流中流线函数与速度势函数的可迭加特性。在流体力学或空气动力学的问题研究中,利用这一特性将某些基本或者已知的平面不可压缩势流的流线函数或者速度势函数的解组合成复杂平面不可压缩势流的流线函数或者速度势函数的解,再利用第7章介绍的求解流体流速方法得出速度解并利用伯努利公式找出压力解,从而获得流动规律,大幅降低求解过程的难度。
式中 φ1、 φ2、 φ3、 …、φn和Φ1、Φ2、Φ3、 … 、Φn分别是简单平面不可压缩势流的流线函数与速度势函数解,而φ和Φ分别是流线函数与速度势函数的组合解,因此平面不可压缩势流具有 φ= φ1+φ2+φ3+…+φn和 φ= φ1+φ2+φ3+…+φn的特性,即在平面不可压缩势流中流线函数与速度势函数的可迭加特性。在流体力学或空气动力学的问题研究中,利用这一特性将某些基本或者已知的平面不可压缩势流的流线函数或者速度势函数的解组合成复杂平面不可压缩势流的流线函数或者速度势函数的解,再利用第7章介绍的求解流体流速方法得出速度解并利用伯努利公式找出压力解,从而获得流动规律,大幅降低求解过程的难度。
8.4.2 问题研究的运算过程
一般而言,问题研究的过程大抵可分成四个步骤,说明如下。
1.找出组合流动的流线函数和速度势函数
平面不可压缩势流可按迭加运算原理将某些基本或者是已知组成流动的流线函数(φ1、 φ2、 φ3、 … 、φn)和速度势函数(Φ1、 Φ2、 Φ3、 … 、Φn)组合成研究问题的流线函数φ和速度势函数Φ,从而进一步求解较为复杂的流动规律。
2.找出组合流动的速度分量
利用第 7 章介绍的求解流体流速方法,从满足平面不可压缩流的判定式∇·V→=0中找出速度分量与流线函数之间的关系式或从满足![]() 的条件找出速度分量与速度势函数之间的关系式,进而获得要研究的流速表达式。
的条件找出速度分量与速度势函数之间的关系式,进而获得要研究的流速表达式。
3.找出组合流动的压力或压力分布情况
从步骤2得到的流速表达式求出流速,再利用伯努利方程获得流体流动的压力或压力分布情况。
4.找出组合流动的运动规律
在平面不可压缩流动问题研究中,只要探讨流体在流场内的流速与压力变化,就可获得流体流动规律。
一般可视问题或研究需要,选择第1~2步或全部步骤依序执行。
8.4.3 均匀等速流与源流的迭加运算
均匀等速流与源流的迭加相当于均匀等速流绕着半无限体的流动,这种类型的迭加运算在工程研究上的推广,就是采用很多不同强度的源流,沿x轴排列,使它和匀速直线流迭加,形成和实际物体轮廓线完全一致或较为吻合的边界流线。这样无须费用巨大的实验,就能初步地估计均匀流体流经物体上游端,例如流经桥墩或门墩的前半部的水流速度和压力分布。
1.组合流动之流线函数与速度势函数的计算与获得
![]()

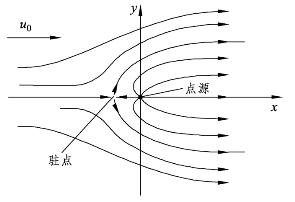
图8-8 均匀等速流与源流迭加后形成的流动
2.组合流动之流速的计算与获得

3.驻点位置的获得

8.4.4 环流与汇流的迭加运算
环流(势涡流)与汇流迭加组成的平面不可压缩势流称为螺旋流(Spiral flow),在旋风燃烧室、离心式喷油嘴和离心式除尘器等设备中,流体自外沿着圆周切向进入,又从中央不断流出,这样的流体流动就类似于环流与汇流的迭加。
1.组合流动之流线函数与速度势函数的计算
假设环流以速度环流量Γ逆时针方向旋转,而汇流以汇流强度q从四周沿着径向方向朝

2.组合流动之流速的计算

3.流线和等势线的示意图

实线代表流线,虚线代表等势线,从图中可以看出流线和等势线是两簇相互正交的对数螺旋线,所以这种流动称为螺旋流。在工程实际上,离心泵、离心风机等的流动类似于环流(势涡流)与源流的迭加形成的组合,是另一类螺旋流,其流动情形如图8-10所示。
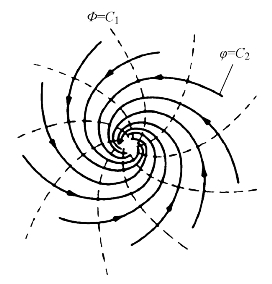
图8-9 环流(势涡流)与汇流迭加形成的流线和等势线
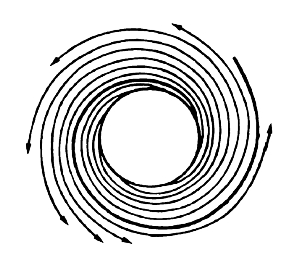
图8-10 环流(势涡流)与源流迭加形成的螺旋流
环流(势涡流)与源流的迭加形成组合流动的流线函数、速度势函数和速度的推导过程与环流(势涡流)与汇流迭加形成之螺旋流类似,这里就不再描述,有兴趣者自行推导与研究。
8.4.5 等强度源流和汇流的迭加运算
对于强度大小皆为 q 的源流和汇流且其源点和汇点分别置于A点位置(-a,0)和B点位置(a,0)两点组成的平面不可压缩势流称为偶流,而如果源点和汇点彼此无限接近,则该组合流动称为偶极流。
1.偶流之流线函数与速度势函数的计算


图8-11 等强度源流和汇流的组合流动中各参数几何关系


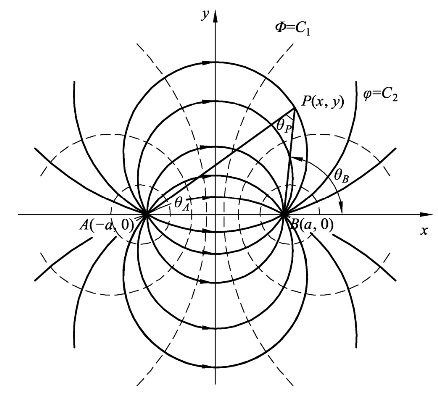
图8-12 等强度源流和汇流迭加所形成之流线和等势线的示意图
2.偶极流的定义与计算

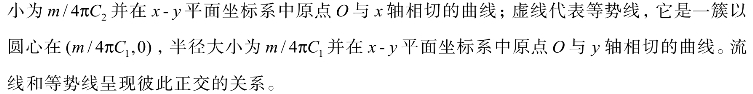
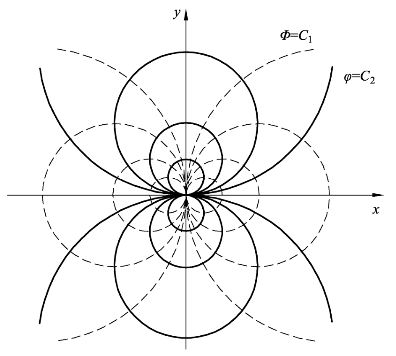
图8-13 偶极流的等势线和流线
【例8-14】
计算强度为![]() 的偶极流在r-θ平面圆柱坐标系的径向速度vr和周向速度vθ是多少?
的偶极流在r-θ平面圆柱坐标系的径向速度vr和周向速度vθ是多少?
【解答】
偶极流的速度势函数Φ和流线函数φ分别是![]() 与
与![]() 因为r-θ平面不可压缩势流径向和周向的速度分量与速度势函数和流线函数之间的关系式分别是
因为r-θ平面不可压缩势流径向和周向的速度分量与速度势函数和流线函数之间的关系式分别是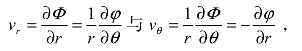 因此偶极流速度分量vr为
因此偶极流速度分量vr为![]() 与
与![]() 。
。
实际上,偶极流本身并无太大的物理及工程实际意义,但它与某些基本的平面不可压缩势流迭加后,可以进一步地利用迭加运算法得到重大实际意义的平面不可压缩位势流的流动解。例如偶极流与等速均匀流迭加可以得到无环量圆柱绕流类型的平面不可压缩位势流,偶极流与等速均匀流和势涡流的迭加可得到有环量的圆柱绕流类型的平面不可压缩位势流。
8.4.6 均匀等速流和偶极流的迭加运算
均匀等速流与偶极流的迭加结果相当于均匀等速流通过无速度环量的圆柱体的平面理想流体流动,其迭加形成组合流动的流线函数和速度势函数的运算、流速的推导如下。
1.组合流动之流线函数与速度势函数的计算

2.组合流动的示意图
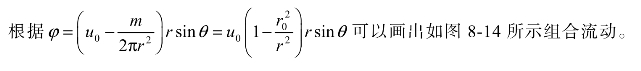

图8-14 均匀等速流和偶极流迭加后的流动
从图中可以看出,φ=0的流线由以x-y平面坐标系的原点O为圆心且半径为0r之圆以及点A、B以外的两轴组成,也就是φ=0的流线自x轴的负端至点A分成两股,沿着上、下两个半圆周至点B时重新汇合后再直朝x轴的正端。流体不能够穿过流线,因此零流线可以用圆柱体的横截面取代。均匀等速流与偶极流的迭加结果就相当于均匀等速流通过无速度环量的圆柱体的平面理想流体流动。
3.均匀等速流通过无速度环量的圆柱体之流速的计算
均匀等速流与偶极流的迭加结果相当于均匀等速流通过无速度环量的圆柱体的平面理想流体流动,因此可以用均匀等速流和偶极流的迭加运算去研究该类型流体流动规律,如图8-15所示。
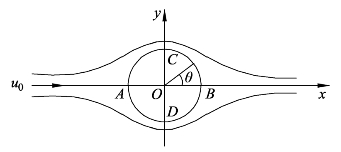
图8-15 均匀等速流通过无速度环量的圆柱体流动


有关工程流体力学基础的文章

根据第 7章以及本章前面内容得到的结果可知,如果流体为平面理想流体,也就是平面不可压缩势流时,流线函数φ和速度势函数Φ两者会同时存在。和均匀等速流类似,源流和汇流也是求解复杂平面理想流体流动时常用的基本平面不可压缩势流流动之一。......
2023-06-29

温馨小提醒事实上,气流与外界环境之间不可能没有热量交换,同时可逆过程也不可能存在。空气流过管道时,在面积 A= 6.5 cm2的截面上,速度 V= 300 m/s ,马赫数为0.6,质量流率 = 1.2 kg/s ,试求该截面上空气的静压和总压。......
2023-06-29

试述调和函数的定义、特性及应用。调和函数的意义。调和函数的特性。工程数学或高等数学发现,如果一个函数u(x,y)为调和函数,则该函数具备“可迭加”的特性。证明如果流体为x-y平面理想流体,流体在流动时的流线函数φ为调和函数,则函数具有迭加性。......
2023-06-29

续表考点1:向量的线性运算1.(2017全国I,13)已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=___________.考点2:平面向量的数量积2.(2014全国I,15)已知A,B,C为圆O上的三点,若=,则与的夹角为___________.1.已知点A(1,-1),B(3,0),C(2,1).若平面区域D由所有满足(1≤λ≤2,0≤μ≤1)的点P组成,则D的面积为_......
2023-10-15

何塞·安东尼奥·科德尔奇西班牙卡尔德斯德斯特拉克;1952年何塞·安东尼奥·科德尔奇是R组,一个第二次世界大战后在巴塞罗那成立的进步建筑师团体的领军人物。欧斯塔基奥·乌加尔德是一名工程师,喜欢一处距巴塞罗那约30公里的地块,靠近卡尔德斯德斯特拉克村,位于山顶,可以俯瞰大海。见过乌加尔德住宅,应当不惊讶于科德尔奇作为摄影师的斐然成就。......
2023-08-20

输入流是用流提取运算符实现的。流读取运算符通常会跳过输入流中的空格、tab键、换行符等等的空白字符。该函数读取num-1个字符后结束,或者遇到分隔符separator时结束。成员函数peek返回输入流中的下一个字符,但并不将其从输入流中删除。......
2023-11-07

在肋梁楼盖中,结构布置包括柱网、承重墙、梁和板的布置。进行结构平面布置时,应综合考虑建筑功能、造价及施工条件等,合理确定梁的平面布置。......
2023-08-30

表4.1.1JavaScript一元运算符(续上表)2.二元运算符二元运算符是指需要两个操作数的运算符,它是JavaScript中最常见的运算符,比如加减乘除、位移、大小比较等。表4.1.2JavaScript二元运算符(续上表)3.三元运算符三元运算符是指需要三个操作数的运算符,JavaScript中唯一的三元运算符是条件运算符(?表4.1.3JavaScript三元运算符有C++开发经验的读者应该知道,C++支持运算符重载,即运算符根据不同的操作数类型执行不同运算。......
2023-11-08
相关推荐