可压缩流体力学中的平面不可压缩势流

2025-09-29 理论教育版权反馈

【摘要】：根据第 7章以及本章前面内容得到的结果可知，如果流体为平面理想流体，也就是平面不可压缩势流时，流线函数φ和速度势函数Φ两者会同时存在。和均匀等速流类似，源流和汇流也是求解复杂平面理想流体流动时常用的基本平面不可压缩势流流动之一。

理想流体流动因为流动的过程中必须同时满足不可压缩流与位势流判定式=0和的假设条件，所以又称为不可压缩势流（Incompressible potential flow）。根据第 7章以及本章前面内容得到的结果可知，如果流体为平面理想流体，也就是平面不可压缩势流时，流线函数φ和速度势函数Φ两者会同时存在。根据理论研究结果，平面理想流体在流动过程中，流线函数与速度势函数这两种函数都属于调和函数，因此两者均具有可迭加的特性，基于此种特性，在研究平面理想流体流动问题时，可以将复杂流体流动的流线函数或速度势函数用简单且已知的流线函数或速度势函数予以迭加表示，然后由其求出流动流体的速度表达式或者流体流动在流场各点的速度，从而找出流体流动的运动规律。平面理想流体流动（平面不可压缩势流）求解的过程中常见的基本流动包含均匀等速流、源流和汇流以及势涡等二维理想流体流动，其流动形态的示意图如图8-1所示。

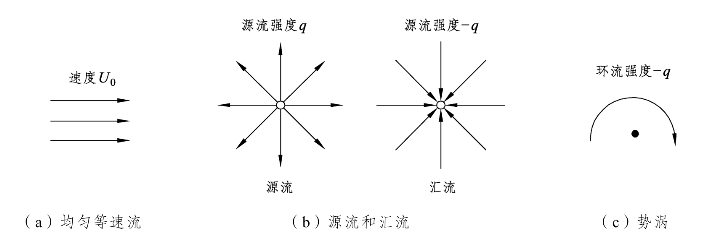
pagenumber_ebook=183,pagenumber_book=176

图8-1 三种基本流动形态

由于流线函数和速度势函数的迭加性，可以利用几种简单流体流动的基本解迭加后获得研究所需的结果，这里针对平面理想流体流动求解过程中常用到的均匀等速流、源流和汇流以及势涡等基本流动解依次加以描述及说明。

8.3.1 均匀等速流

均匀等速流为求解复杂平面理想流体流动时常用的基本平面不可压缩势流之一，重点在于流体流动类型的定义以及流线函数φ和速度势函数Φ的获得。

1．均匀等速流的定义

pagenumber_ebook=183,pagenumber_book=176

2．流线函数的计算与获得

pagenumber_ebook=184,pagenumber_book=177

3．速度势函数的计算与获得

pagenumber_ebook=184,pagenumber_book=177

4．流线和等势线的示意图

根据流线函数φ与速度势函数Φ计算式，可以画出均匀等速流的流线和等势线，如图8-2所示。实线为流线，虚线为等势线，从图中可以看出，流线和等势线呈现相互垂直的关系，也就是两者彼此正交。

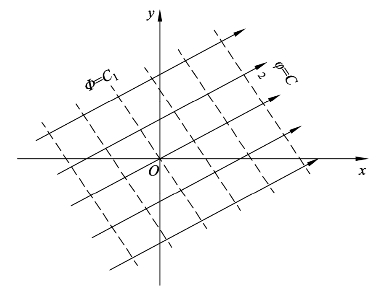
pagenumber_ebook=184,pagenumber_book=177

图8-2 均匀等速流之流线和等势线的示意图

5．讨论

对于一个平面理想流体均匀等速流，流场内各点的速度都相同，所以根据伯努利方程式可以推知，如果均匀等速流是在水平面上或者重力对流体流动造成的影响忽略不计，则流动流体造成的静压P为一个特定常数，也就是P=C。

【例8-6】

如果流体为x-y平面理想流体均匀等速流，且流速平行于 x 轴，也就是流速表达式为，试求流线函数φ与速度势函数Φ的表达式。

【解答】

pagenumber_ebook=185,pagenumber_book=178

【例8-7】

如果流体为x-y平面理想流体均匀等速流，且流速平行于y轴，也就是流体的流速表达式为试求流线函数φ与速度势函数Φ的表达式。

【解答】

pagenumber_ebook=185,pagenumber_book=178

8.3.2 源流和汇流

研究平面理想流体流动时，可以使用基本平面理想流体流动（基本平面不可压缩势流）的流线函数与速度势函数构建出复杂流体流动的流线函数或速度势函数，进而求出流体流动的速度表达式。和均匀等速流类似，源流和汇流也是求解复杂平面理想流体流动时常用的基本平面不可压缩势流流动之一。

1．源流和汇流的定义

如图8-3所示，二维的源流和汇流是指从平面内的一点（即O点）沿着径向均匀且直线地流向四周或者从四周流入，且流体流速与半径成反比的流动形态。如果流动以一定的强度从O点沿着径向方向均匀且直线地向四周流出，这种流动称为源流（Source flow），而O点称为源点（Source point）。如果流动以一定的强度从各方沿着径向方向均匀且直线地流入O点，这种流动称为汇流（Sink flow），而O点称为汇点（Sink point）。

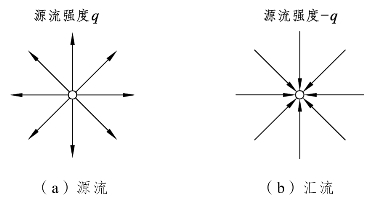
pagenumber_ebook=186,pagenumber_book=179

图8-3 源流和汇流的示意图

2．源流和汇流的强度

源流和汇流的强度是指流体从源点或汇点通过半径为 r 的每单位长度圆柱面流出或流入的流量，用符号q表示。由其定义可知 q=±2 π rvr，式中vr为沿径向方向的速度分量。如果q值为正，流体流动的形态是源流，也就是流体是从源点O沿着径向流向四周；如果q值为负，流体流动的形态是汇流，也就是流体是从四周沿着径向方向流向汇点O。

3．源流和汇流的速度分量

根据源流、汇流及其强度的定义可以推知，源流和汇流在径向方向的速度分量是而在周向方向的速度分量vθ=0。所以源流和汇流问题必须使用r-θ平面圆柱坐标来处理。

4．源流和汇流的速度表示法

pagenumber_ebook=186,pagenumber_book=179

【例8-8】

请用r-θ平面圆柱坐标的速度表示法表示源流的速度。

【解答】

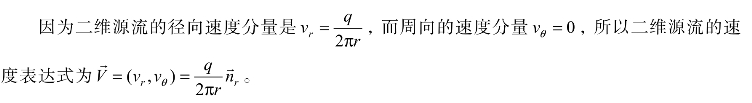
pagenumber_ebook=186,pagenumber_book=179

【例8-9】

证明二维源流存在流线函数φ。

【解答】

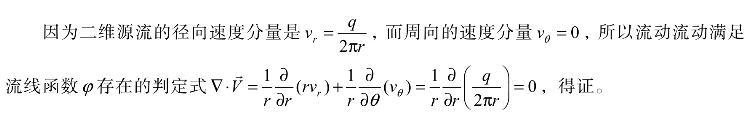
pagenumber_ebook=187,pagenumber_book=180

【例8-10】

证明二维源流存在速度势函数Φ。

【解答】

pagenumber_ebook=187,pagenumber_book=180

5．源流和汇流之流线函数的计算(https://www.chuimin.cn)

pagenumber_ebook=187,pagenumber_book=180

6．源流和汇流之速度势函数的计算

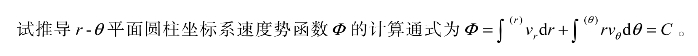
pagenumber_ebook=188,pagenumber_book=181

【例8-11】

pagenumber_ebook=188,pagenumber_book=181

【解答】

pagenumber_ebook=188,pagenumber_book=181

7．流线和等势线的示意图

根据源流和汇流的流线函数φ与速度势函数Φ计算式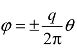 pagenumber_ebook=188,pagenumber_book=181 和可以画出源流和汇流的流线和等势线，如图8-4 所示。图中实线代表流线，虚线代表等势线。如果流体是从O点沿着径向方向流向四周，则流动的形态是源流。如果流体是从四周沿着径向方向流向O点，则流动形态是汇流。

8．讨论

pagenumber_ebook=188,pagenumber_book=181

pagenumber_ebook=189,pagenumber_book=182

图8-4 源流和汇流之流线和等势线

（1）源流和汇流的源点和汇点为奇点。当半径r=0时，源流和汇流的径向速度vr会变成正无穷大或负无穷大，所以源流和汇流的源点和汇点是奇点。径向速度的计算公式只有在源点或汇点以外的区域才能应用。

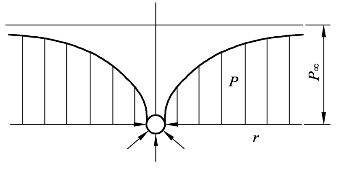
pagenumber_ebook=189,pagenumber_book=182

图8-5 源流和汇流沿径向之压力P分布

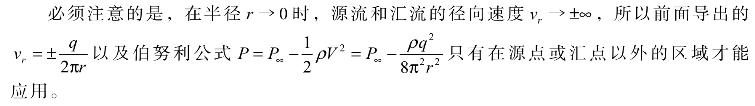
pagenumber_ebook=189,pagenumber_book=182

8.3.3 势涡流

势涡流又称为环流或自由涡流，它和前面介绍的均匀等速流与源流和汇流一样，也是利用迭加法求解复杂平面理想流体流动时常用的基本不可压势流之一。

1．势涡流的定义

如图8-6所示，势涡流（Potential vortices）是指流体以一定环流强度绕着某一固定点O做均匀且等速的圆周运动，流体流速与圆周半径成反比的流体流动形态。

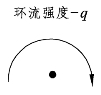
pagenumber_ebook=190,pagenumber_book=183

图8-6 势涡流形态

根据开尔文定理（Kelvin theorem），对于无黏性流体，如果初始时刻为无旋的流动将永远保持无旋，而有旋流动的涡流强度Γ则具有保持性，既不会消失，也不会扩散，流动必定满足的关系。由此可知，在平面理想流体（二维不可压缩非黏性流）的假设中，势涡流的环流强度Γ保持为一个常数。由于势涡流假设在没有外力的情况下始终存在，所以势涡流也称为自由涡流（Free eddy current）。

2．势涡流的环流强度

势涡流的环流强度（Potential vortex strength）Γ又称为势涡流的速度环流量（Velocity circulation of potential vortex），它定义为速度对周围曲线的线积分，也就是并以逆时针的方向为正，也就是如果Γ＞0，则势涡流为逆时针旋转，如果Γ＜0，则势涡流为顺时针旋转。

3．平面势涡流的速度向量表示法

pagenumber_ebook=190,pagenumber_book=183

【例8-12】

说明环流（平面势涡流）存在速度势函数Φ。

【解答】

（1）因为环流（平面势涡流）在径向和周向的速度分量分别是 vr=0和 pagenumber_ebook=190,pagenumber_book=183 所以平面势涡流的流动问题必须使用r-θ平面圆柱坐标系来处理。

（2）因为无旋流的判定式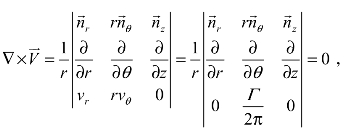 pagenumber_ebook=191,pagenumber_book=184 所以环流（平面势涡流）存在速度势函数Φ。

（3）从步骤（2）可知，环流（平面势涡流）是无旋流，也就是说环流是圆周运动，却不是有旋运动。

4．平面势涡流之流线函数的计算

pagenumber_ebook=191,pagenumber_book=184

5．平面势涡流之速度势函数的计算

pagenumber_ebook=191,pagenumber_book=184

6．流线和等势线的示意图

根据平面势涡流之流线函数φ和速度势函数Φ的计算式 pagenumber_ebook=191,pagenumber_book=184 和可以画出平面势涡流的流线和等势线，如图8-7 所示，实线代表流线，虚线代表等势线。从图中可以看出，流线是不同半径的同心圆，也就是圆周半径 r 相同时，速度势函数Φ=常数的圆形曲线；等势线是不同圆心角的径线，也就是圆心角θ相同时，流线函数φ=常数的直线。所以能够推知，平面势涡流的流线函数与速度势函数两者呈正交的关系，除此之外，如果环流强度Γ＞0，则势涡流为逆时针旋转，如果环流强度Γ＜0，则势涡流为顺时针旋转。