流线函数与速度势函数在流体力学中的作用

这里引入流线函数与速度势函数的概念，用来求解二维流场的速度分布情况，流线函数与速度势函数在工程上对流体流动问题的研究占有极其重要的地位与作用。例如在平面不可压缩流体以及无旋流体的流动问题中，可以先从流线函数或速度势函数求出速度场，再应用伯努利方程求得压力场，如此使研究问题的难度大幅地降低。

7.4.1 流线函数

流线函数在早期平面不可压缩势流理论问题的研究中占有非常重要的地位，因为使用流线函数可以求解二维理想流体的流速变化，从而获得流场内的压力变化，并进一步找出二维理想流体的运动规律。

1．流线函数的定义与存在条件

流线函数（Stream function）是二维不可压缩流体流动过程的质量守恒微分方程形式，也就是从连续微分方程∇·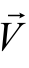=0推导而得的一个特殊函数。这里以x-y二维不可压缩流场为例说明该函数的定义、推导方式以及推导过程中得到的几个推论。

2．流线函数的应用

根据流线函数φ的定义，可以利用流线函数求得流体流速的速度分量从而描述流体在二维不可压缩流场内的速度分布，或者从二维不可压缩流场的速度表达式或速度分量中求得流线函数。

【例7-19】

试说明流线函数存在条件与是否存在判定方程式。

【解答】

（1）如果流体流场是二维不可压缩流场，则流线函数φ必定存在，因此可以推知，流线函数存在条件是流体流场必须是一个二维（平面）不可压缩流场。

（2）因为流线函数的存在条件是流体流场必须是一个二维（平面）不可压缩流场，而如果流场是二维（平面）不可压缩流场，则流体流速必须满足二维质量守恒微分方程或二维连续微分方程因此可以推得，流线函数是否存在的判定为是否为0。如果则流线函数存在；如果则流线函数不存在。

【例7-20】

如果流场为稳态，流动速度为，是否存在流线函数φ？为什么？

【解答】

【例7-21】

【解答】

【例7-22】

【解答】

7.4.2 速度势函数

速度势函数是从无旋流场中推导出来的，和流线函数一样，在早期的平面不可压缩势流理论研究中占有非常重要的地位。利用速度势函数可以求解二维理想流体的流速变化，从而获得流场内的压力变化，并进一步找出二维理想流体的运动规律。

1．旋涡的基本理论

在生活中经常看到流体做明显的旋涡运动，如龙卷风、台风或小旋风等都是旋涡运动，它是一种强烈的有旋运动。在自然界和工程领域中旋涡的例子不胜枚举，例如在大气和海洋中的环流以及工程领域中飞行器、发动机燃烧室、锅炉燃烧室、流体机械、桥梁与各种水利设施等涉及流动时可以看到大量的旋涡运动。

（1）流体微团的运动分析。在流体力学的问题研究中经常提到流体质点和流体微团这两个名词，是基本概念，初学者容易搞混，这里对其定义进行说明与区分。

① 流体质点与流体微团的定义与区别。通常研究流体力学问题时并不讨论个别分子的微观行为，而是以宏观的观点去研究的流体运动，也就是假设流体由无限流体质点或流体微团组成，流体质点和流体微团的最大差异是流体质点是指微小体积内所有流体分子的总称，它是可以忽略在受力时产生线性尺度效应的最小单元，而流体微团则是由多个流体质点组成的具有线性尺度效应的微小流体团。简单地说流体微团（Fluid micromass）是由多个流体质点（Fluid particle）组成，而流体流动是由无限多个流体质点或流体微团的运动综合，充满运动流体的空间即称为流体流场。由于流体质点的定义，其在运动时产生的内效应，也就是变形效应可以忽略不计，其假设与理论力学的问题研究中，刚体受力时可以忽略作用力对物体造成伸长、缩短或弯曲等效应的道理类似。

② 流体质点与流体微团的运动分析。在理论力学的问题研究中，刚体的运动可分为平移和转动两种形式。流体与刚体的不同主要在于流体具有流动性，极易变形，流体微团运动过程中，除了与刚体一样可以平移和转动之外，还会发生变形，而流体产生的变形运动能够分成线变形和角变形（剪切变形）两种类型如图7-14所示。

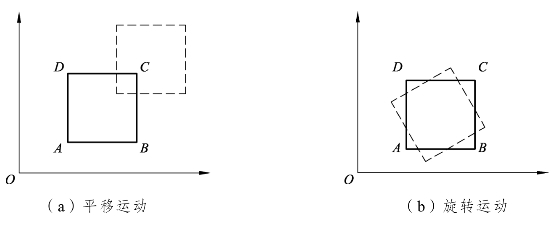
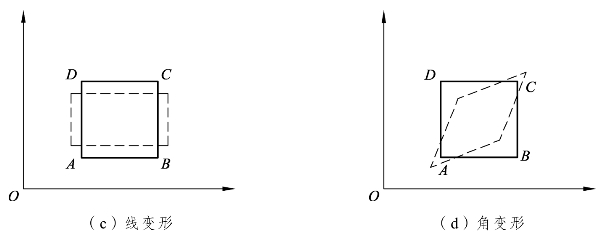
图7-14 流体运动类型示意图

在工程计算中，为了简化问题经常使用理想流体（Ideal fluid）的假设——假设流体的压缩性与黏性忽略不计，因此流体微团在流动时线变形和角变形（剪切变形）均可以忽略不计。如果流体没有黏性，则不存在剪应力，就无法传递旋转运动。所以在理想流体的假设中，流体微团或流体质点的运动，只有平移运动，而没有旋转运动和变形运动。可以推知，在理想流体假设中，流体流动时只改变流体微团或流体质点的位置而不改变其形状、大小和方向。

【例7-23】

试论述刚体和流体微团的运动构成类型的差异。

【解答】

（1）在理论力学问题研究中，刚体是指在力的作用下其大小和形状都不变的物体，也就是假设物体（固体）在受力时物体不会变形，因此只有平移运动和旋转运动两种方式。

（2）根据亥姆霍兹速度分解定理在一般情况下，流体微团的运动由平移、旋转、变形（线变形和角变形）等类型构成。

【例7-24】

问流体质点与流体微团的定义如何？其运动构成类型的差异性如何？为何在理想流体的假设中，流体质点与流体微团两者的运动构成类型会一致？

【解答】

（1）在流体力学问题研究中，流体质点是指在可以忽略受力时产生线性尺度效应的微小体积内所有流体分子的总体，流体微团则是由多个流体质点组成的具有线性尺度效应的微小流体团。

（2）一般情况下，流体微团的运动由平移、旋转、变形（线变形和角变形）等构成，而流体质点因为线性尺度效应可以忽略不计，因此不考虑变形运动，只有平移运动和旋转运动两种类型。

（3）在理想流体的假设中，流体的压缩性与黏性忽略不计，因此流体微团在流动时的线变形和角变形（剪切变形）均可以忽略不计。如果流体没有黏性，则不存在剪应力，就无法传递旋转运动、所以在理想流体的假设中，流体微团和流体质点两者的运动都只有平移运动。

2．无旋流的定义与存在条件

如果流体在某特定研究区域的涡度（Ω）均为0，则该流体在流场中的流动称为无旋流。实际的流体都不会是无旋的，只有假设无黏性流体的流动才有可能是无旋流，那是因为如果流体没有黏性，自然不存在剪应力，也就不能传递旋转运动。根据无旋流的定义以及有关流体旋度的内容描述，可以推知，一个流体流场是否为无旋流的判定方程为如果则流场是无旋的，如果则流场是有旋的。无旋流动的唯一标志是流体微团并没有旋转，它与流体运动的轨迹形状无关。如图7-15 所示流体微团运动，（a）和（b）的运动轨迹是直线，（a）是无旋流，而（b）是有旋流；（c）和（d）中的运动轨迹是圆周，（c）是无旋流，而（d）是有旋流。由此可以发现，流体是否为无旋流动取决于流体的涡度或流体微团的旋转角速度是否为0。

图7-15 流体微团无旋或有旋运动的示意图

【例7-25】

【解答】

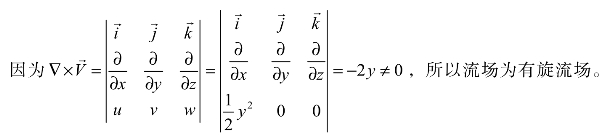
3．位势流的定义与无旋流的关系

一般而言，在流体力学的问题研究中，位势流（Potential flow）指的就是无黏性流（Inviscous flow），它是一种假想的流场。无黏性流假设流体流动时不会受到流体黏性的影响，也就是指流体绝对黏度μ=0的流动。如果流体的流动为无黏性流，流场的速度位势（Velocity potential）不会因为受到流体黏性的影响而衰减，在流体流动的过程中将会是一个常数。根据本章“无旋流的定义与存在条件”的内容描述，无旋流存在条件也是假设流体流动过程为无黏性流，涡度也不会受到流体黏性的影响而衰减，流场的涡度也将保持是一个常数。可以推知，在流体力学中，位势流、无旋流与无黏性流三者代表的物理意义与假设是相同的，也就是流体的绝对黏度μ=0时，流体的涡度以及速度位势维持不变。

4．速度势函数的定义与存在条件

【例7-26】

试说明速度势函数Φ的存在条件与判定方程式。

【解答】

（1）速度势函数的存在条件：如果流体流动的过程是无旋流也就是位势流，则速度势函数Φ存在。

（2）根据无旋流或者位势流判定方程可以推得速度势函数存在的判定方程式是∇×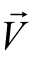为0。从前面例题可知，无旋流、位势流、无黏性流、有势流动以及速度势函数存在与否的判定式均为∇×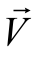是否为0。

5．判定式的计算

【例7-27】

如果流体流场的速度分量分别为 u=x2 +y2，v =-2 xy+3x ，问是否存在速度势函数Φ？

【解答】

因为所以流体流场为有旋流场，速度势函数Φ也就不存在。

6．速度势函数的应用

在流体力学与空气动力学问题研究中，可以根据速度势函数Φ的定义，利用速度势函数求得无旋流场内的速度分布或者从无旋流场内的速度表达式或其速度分量中求得速度势函数。

【例7-28】

如果二维无旋流场且其速度势函数表达式为 Φ=4(x 2+y2)，问该流体流场流动时的速度表达式是什么？

【解答】

【例7-29】

若流场为x-y二维无旋，已知流场的滞止压力P为101 000 Pa，流体的密度ρ为ρ= 1.19 kg/m3，平面势流的速度势函数表达式为 Φ= (x 2 - y2)，试求流动流体在流场内点（2，1.5）处的速度值与压力值。

【解答】

【例7-30】

【解答】

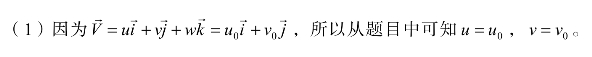
7.4.3 流线函数与速度势函数的关系

如前所述，流线函数φ必须在二维不可压缩流场的条件下才能够存在，流体流动的过程必须满足的判定方程式。而速度势函数Φ必须在流体流场为无旋流场的条件下才能够存在，流体流动的过程必须满足的判定方程式。所以流线函数φ和速度势函数Φ必须在二维不可压缩的无旋流场才能够同时存在，也就是流体的流场必须是平面理想流体的流场，它是一个假想情况。研究证明，如果流线函数φ和速度势函数Φ同时存在，则流线函数和速度势函数两者彼此正交。

【例7-31】

如果流场为x-y二维不可压缩流场与非旋性流场，试证明流线函数φ与速度势函数Φ彼此正交。

【解答】

【例7-32】

何谓位势流？何谓速度势函数？如何由速度势函数得到流场的速度分量？在流体力学与空气动力学的问题研究中，速度势函数与流线函数在应用范围的主要差异性是什么？

【解答】

（1）在流体力学与空气动力学的问题研究中，所谓位势流指的是无旋流，也就是流体流动的过程满足= 0的判定方程式，因此可找出速度势函数Φ的存在。又因为如果流体的流动为无黏性流，流场的速度位势不会因为受到流体黏性的影响而衰减，所以速度势函数会是一个常数。位势流也是指流体在流动的过程中满足绝对黏度μ=0假设。

（2）因为位势流指的是无旋流，流体流动的过程满足的条件，因此可以找到一个函数Φ使得流场的速度并由此计算公式，可以得到流场的速度分量。

（3）在工程应用中，可以使用速度势函数Φ求得无旋流的速度分量，而使用流线函数则是为了求得二维不可压缩流的速度分量。

【例7-33】

在流体力学与空气动力学的问题研究中，流线函数φ与速度势函数Φ同时存在的条件是什么？如果流线函数与速度势函数同时存在，两者的相互关系是什么？

【解答】

（1）同时存在的条件：流线函数φ与速度势函数Φ必须在二维不可压缩的无旋流场才能够同时存在，也就是流体流动过程必须满足与的条件。因此流动流体必须为二维的理想流体，也就是流体流动过程必须是二维流动且同时满足流体密度ρ=C与绝对黏度μ=0的条件。

（2）相互关系：如果流体流场同时存在流线函数φ和速度势函数Φ，则流线函数与速度势函数彼此之间呈垂直的关系，也就是流线函数与速度势函数两者彼此正交。

课后练习

（1）控制体积法的类型与研究目是什么？

（2）说明积分控制体积法与微分控制体积法的优缺点。

（3）列出雷诺转换公式并说明其代表的物理意义。

（4）列出质量守恒积分方程式并说明其代表的物理意义。

（5）如图7-16 所示，如果玻璃球可以由截面1充气，其截面积为 A1，速度为V1，密度为 ρ1，玻璃球的半径为R，问玻璃球在充气过程中的质量流率表达式是什么？

图7-16 玻璃球充气

（6）如图7-17所示，从喷管喷出密度为ρ及速度为V的水流冲击到一个具有转向角β且以稳定的速度U移动的叶片，假设叶片安装在导轨上受到一个约束力F作用，问水柱流经进出口截面的流量（体积流率）表达式是什么？

（7）列出动量守恒积分方程并说明其代表的物理意义。

（8）如图7-17所示，从喷管喷出密度为ρ及速度为V的水流冲击到一个具有转向角β且以稳定的速度U移动的叶片，假设叶片安装在导轨上受到一个约束力F作用，问水柱冲击力的表达式是什么？

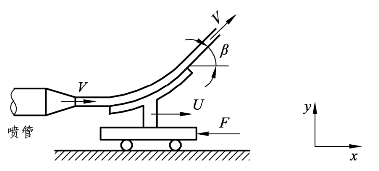
图7-17 水流冲击移动叶片

（9）分别列出喷射（气）发动机净推力公式与总推力公式并说明其差异。

（10）列出涡喷发动机的主要影响因素。

（11）问涡喷发动机的进气量对发动机推力的影响如何？

（12）问涡喷飞机的飞行高度对发动机推力的影响如何？

（13）问流线函数φ的存在条件是什么？

（14）问速度势函数Φ的存在条件是什么？

（15）问不可压缩流场的判定条件是什么？

（16）问无旋流场的判定条件是什么？

（17）如果二维流场的速度分量u=x与v=-y，问流线函数φ与速度势函数Φ是否存在？

（18）问流体的流场同时存在流线函数与速度势函数的条件是什么？

（19）问如果流体的流场同时存在流线函数与速度势函数，两者的关系是什么？

（20）如图7-18 所示，考虑水（ρ=1×103 kg/m3）稳定地流经装置。各截面面积分别是A1=0.018 6 m2、 A2=0.046 5 m2及 A3=A4=0.037 2 m2，而水流经截面①的速度为3.048 m/s，通过截面③的质量流率为56.624 kg/s，通过截面④的体积流率为0.093 m2/s。假设通过各进出口管路皆为均匀流动，试求水流经②截面积的质量流率和流速是什么？

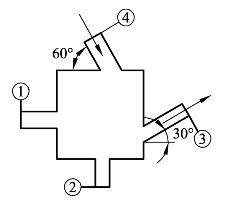
图7-18 水流经多截面管道

（21）如图7-19所示，静态推力测试台是用来测试喷射（气）发动机的静态推力装置，如果某喷射（气）发动机的测试数据为 V1=200 m/s、 V2=500 m/s、 P1=78.5 kPa、P2=101 kPa、 A1=1.0 m2以及T1=268 K ，问该喷射（气）发动机的推力如何？

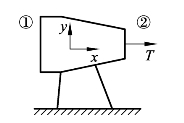
图7-19 静态推力测试台

（22）已知密度为ρ的不可压缩无黏性流体，以均匀流速U0流经一个圆柱（二维），其流线分布可用流线函数表示，问流动流体在x轴方向的速度分量是什么？

（23）若流场为x-y二维无旋流场，速度势函数的表示式为 Φ= 4(x 2+y2)，问流动流体在x轴方向的速度分量是什么？