一个逻辑函数的真值表是唯一的，但函数表达式可以有多种形式。对逻辑函数进行化简，求得最简表达式，可使实现逻辑函数的逻辑电路及问题的分析简单化，在工程上可以做到节省元器件、提高电路的可靠性。逻辑函数化简有公式法和卡诺图法两种。例如，逻辑函数式可以有五种表达式，其转换方法如下：原式是与或表达式。......
2023-06-24
积分控制体积法：诺转换公式的应用与简化
【摘要】：积分控制体积法使用的计算方程为诺转换公式，关注的重点是转换公式的应用以及公式的推导和简化。诺转换公式的目的是将整个流体质量系统转换成控制体积系统的物理量分析。
积分控制体积法使用的计算方程为雷诺转换公式，关注的重点是转换公式的应用以及公式的推导和简化。工程计算中经常使用的是质量守恒方程与动量守恒方程，描述如下。
7.2.1 雷诺转换公式
基于流体力学问题研究特性，处理流体流动问题时先将整个流体系统的质量、动量以及动量矩等分析转换成流体在特定研究区域的相应物理量的分析，也就是将第6章内容提及的控制质量系统（Control mass system）转换成控制体积系统（Control volume system）。如果要达到此目的，就必须将物理量的计算方程转换成适合于某特定研究区域内，而非某个固定质量系统的计算方程，这种转换用到的定理称为雷诺转换定理（Reynolds transformation theorem）。换句话说，雷诺转换定理在研究流体运动时，扮演着将流体在整个流体质量系统内物理量分析转换成在控制体积系统内的角色。这定理能够运用于所有基本定律的转换，而用到的公式即称为雷诺转换公式（Reynolds transformation equation）。由于积分控制体积法中使用的计算方程都由雷诺转换公式推导而出，雷诺转换公式又称为一般守恒方程式（General conservation equation）。
1．公式介绍
2．公式代表的物理意义
3．雷诺转换公式的应用
雷诺转换公式在流体力学与空气动力学中多应用于质量守恒方程与动量守恒方程的转换。
【例7-1】
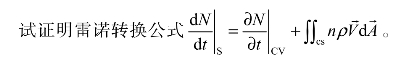
【解答】
【解答】
（1）雷诺转换公式的目的是将整个流体质量系统转换成控制体积系统的物理量分析。它是一种将流体流动问题的计算锁定在研究者关注的区域以探讨物理量变化之计算思维的转换方式。
（2）在雷诺转换公式中各项代表的物理意义如下。
①
：物理量N的全变化率，也就是流体质量系统中物理量N随时间的变化率。
②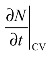
：局部的物理量N随时间变化率，也就是流体在研究区域或控制体积中物理量N的累积率。
③
物理量 N 进出控制系统引起的变化率，也就是流体通过控制体积表面或研究区域表面的物理量N流出率的总和。
7.2.2 质量守恒方程式
质量守恒方程源于质量本身不可创造或毁灭原理并利用雷诺转换定理进行转换推导而得的有关流体在研究区域表面或控制体积内质量变化率公式。根据流体的连续性，在工程计算中，流体可视为一个连续且没有空隙的介质，所以质量守恒方程又称为连续方程式（Continuity equation）。质量守恒方程多用来处理流体在控制体积（研究区域）内质量变化率，控制体积（研究区域）表面，也就是控制表面或边界上的质流率、体流率和流体密度、速度，以及经有效截面的物理量计算问题。
1．公式推导
2．物理意义
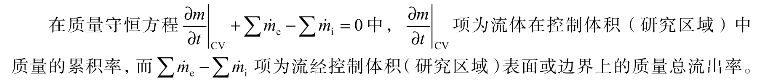
3．简化与应用
质量守恒方程根据流体流动的类型分为非稳态可压缩流动问题、非稳态不可压缩流动问题、稳态可压缩流动问题以及稳态不可压缩流动问题四类的计算。
（1）非稳态可压缩流体流动问题。
【例7-3】
如图7-3所示，不可压缩流体在半径为R的圆管进口处速度为V1，经过一定距离，在管内以速度
作稳定的层流流动，试求
图7-3 圆管内层流流动
（1）流体经过调适后的平均速度。
（2）V1与Vmax之间的关系。
【解答】
【例7-4】
如图7-4所示，如果玻璃球由截面1充气，其截面积为 A1，速度为V1，密度为 ρ1，玻璃球半径为R，试求玻璃球内密度 ρb(t)的瞬时变化率。
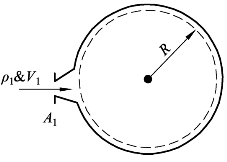
图7-4 玻璃球进气
【解答】
（1）玻璃球在充气过程中，球内气体的质量会越来越多，密度也就越来越大，所以在玻璃球内空气质量随着时间的改变与密度的变化不可以忽略，这问题属于非稳态可压缩流动问题类型。
（2）因为质量守恒方程式
，且玻璃球内气体的质量为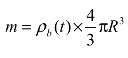
。
【例7-5】
如图7-5 所示，假设桶内（控制体积）所装液体为水，试写出其流动过程中的质量守恒方程与该方程代表的物理意义。
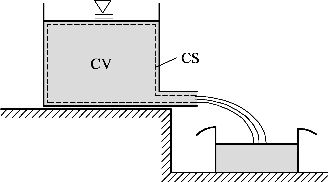
图7-5 桶里装水流动
【解答】【例7-6】
如图7-6 所示，假设桶内所装液体为水，桶的面积是 A，流出孔的面积是 A1，水面的高度是h，水流出的速度是V，试推导桶内水流时间t与高度h和水流速度V的关系式。
图7-6 桶内水流动
【解答】
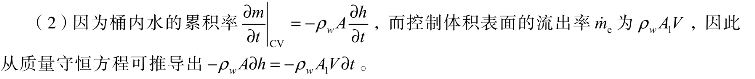
【例7-7】
空气流过单一进出口的工程管道时，截面面积 A= 6.5 cm2，速度 V= 300 m/s ，马赫数＝0.6，质量流率 
= 1.2 kg/s ，试写出流体质量守恒方程并求出该截面上空气的静压P值。
【解答】
（1）因为气体的流速大于 0.3 马赫（Ma），必须考虑空气的密度变化，而工程计算中常将流体流动过程视为稳态问题，因此这属于稳态可压缩流动类型问题，流体质量守恒方程可写成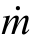
=ρAV =C 。
【例7-8】
如图7-7 所示，如果空气在管道中的流动为一个稳态可压缩流动过程，试写出流场内密度ρ、比容γ、面积A以及速度V之间的关系式。
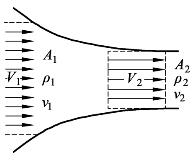
图7-7 管道流动
【解答】
【例7-9】
如图7-7 所示，如果空气在管道中的流动为稳态不可压缩流动过程，试写出流场内面积A和速度V之间的关系式。
【解答】
【例7-10】
如图7-8 所示，从喷管喷出的水流密度为ρ，速度为 V射流冲击到一个具有转向角β且以稳定的速度U移动的叶片，假设叶片安装在导轨上受到力 F，问水柱流经进出口截面的质量流率表示式是什么？
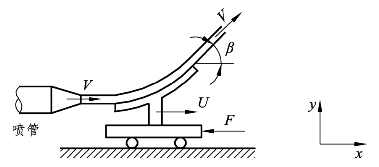
图7-8 喷流冲击移动叶片
【解答】
7.2.3 动量守恒方程式
动量守恒方程是物理学中动量定理在流体力学中的具体表现，它反映了流体流动过程中的动量变化以及流动产生的作用力和作用力造成的影响。动量守恒方程是利用牛顿第二运动定律并由雷诺转换定理进行转换推导而得流动作用力的计算公式。在工程实际中，动量守恒方程多用于处理流动与控制体积之间相互作用力的计算，例如流动对弯管的作用力或者射流对平板的冲击力等问题的计算都使用动量守恒方程。
1．公式推导
2．物理意义
动量守恒方程式
代表的物理意义为“作用在控制体积的力总和等于流体流经控制表面或研究区域表面的动量总流出率”。由于流体动量与流动产生的作用力为向量，而非标量，所以由雷诺转换公式推导出的动量守恒方程为向量，而非标量。在实际的工程计算中，建议先选定一个坐标系，以便找出各个作用力在控制体积各方向的分量大小及作用方向，与流经控制表面的各部分动量通量的关系。
【例7-11】
【解答】
【例7-12】
【解答】
【例7-13】
如图7-9所示，静态推力测试台是设计用来测试喷射（气）发动机（Jet engine）的静态推力装置，如果某喷射（气）发动机的测试数据为 V1=200 m/s 、V2=500 m/s、 P1=78.5 kPa、P2=101 kPa、 A1=1.0 m2以及T1=268 K ，问该喷射（气）发动机的质量流率与推力是多少？
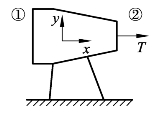
图7-9 静态推力测试台
【解答】
（1）设定问题研究的假设以方便求解：假设问题中流动的过程为稳态一维流动。
① 确定控制体积与其上的作用力。如图7-10所示，控制体积的取法如虚线所示区域范围。流动产生作用于控制体积上的作用力，包括推力以及流体压力在截面①与截面②上产生的作用力。
图7-10 确定静态推力测试台控制体积及作用力
【例7-14】
如图7-11所示，密度为ρ、速度为V1和流量（体积流率）为Q的自由射流冲击到静止的板上，水流向四周散开，假设截面2和截面3的截面面积分别为 A2和 A3以及流经截面2和截面3平均流速分别为V2和 V3，且 A2=A3=A1/2以及V2=V3，试求图中（a）和（b）的射流对挡板的冲击力。自由射流指从喷管或者孔口射入大气的一股流束，特点是流束上的压力为大气压力。
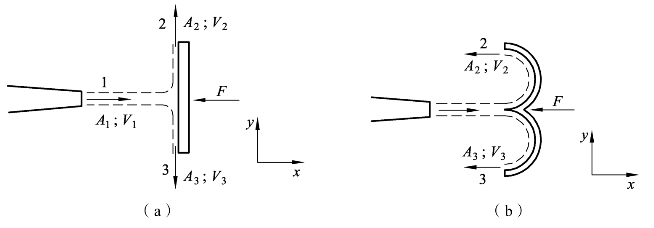
图7-11 射流冲击静止板
【解答】
（1）设定问题研究的假设以方便求解：假设流动过程是稳态，并忽略重力效应以及射流运动时的机械能损失。
（4）比较图（a）与图（b）中射流对挡板冲击力的计算结果可以发现，图（b）中射流对反向曲面产生的冲击力是图（a）中平板的两倍，所以为了充分利用水流的动力，在冲击式水轮机上采用反向曲面作为叶片形状，不过为了回水方便，反向角通常采用160°～170°。
【例7-15】
如图7-12所示，从喷管喷出密度为ρ及速度为V的水流冲击到一个具有转向角β且以稳定的速度U移动的叶片，假设叶片安装在导轨上并受到一个约束力F，请问约束力F做功最大时的U/V值是多少？
图7-12 水流冲击移动的叶片
【解答】
（1）设定问题研究的假设以方便求解：假设流体流动的过程是稳态流动，并忽略净压力作用与重力效应以及射流运动时产生的机械能损失，并假设水柱沿着叶片经过的截面积为定值，因此沿着叶片水流的平均速度为均值。
（2）确定控制体积与其上的作用力：控制体积的取法如图7-13中虚线所示区域范围，因叶片为水平移动，所以可以推知控制体积受到y方向的作用力为0，也就是 Fy=0。
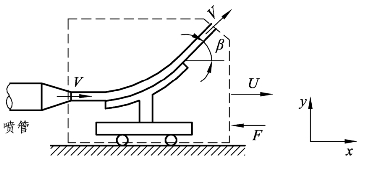
图7-13 水流冲击问题的控制体积选取
3．涡轮喷射发动机的推力
（2）公式计算结果相同的必要条件。
通过涡轮喷射发动机推力公式中净推力公式与总推力公式的比较，可以发现只有在当飞行空速 Va等于0时，净推力公式计算结果才与总推力公式计算结果相等。喷气式飞机在维修过程中地面试车阶段会使用钢绳固定在喷气式飞机的尾部避免飞机移动，防止飞机突然向前冲出造成人员、装备以及飞机本身的损伤，此时飞机飞行速度自然为0。把涡射发动机拆下来放在试车台上测试，当然也不会有飞机飞行速度。因此不论喷气式飞机在地面试车或涡喷发动机在试车台试车，飞机飞行速度Va等于0，发动机总推力自然等于净推力。据此，得出结论：涡喷发动机的净推力公式与总推力公式计算结果相同的必要条件是飞机飞行速度为0，也就是飞机在静止的时候，净推力公式与总推力公式的计算结果才会相同。一般情况下，只有喷气式飞机在地面试车或者把涡喷发动机拆下来放在试车台试车时，净推力才会等于总推力。
（3）影响推力的因素。
涡喷发动机推力受到空气质量流率、飞机飞行速度、喷气（射）速度以及喷管出口面积的影响。空气质量流率受飞机飞行高度以及大气的密度、温度、压力和湿度等因素影响，且喷气（射）速度又是发动机转速的函数。因此涡喷发动机的影响因素包括发动机进气量、转速与发动机喷管出口面积、飞机飞行高度与飞行速度以及飞机飞行时的大气密度、温度、压力与湿度等。这些因素与推力的关系受限于篇幅且多属航空发动机的课程范围，通常不在流体力学中讨论，学生可以自行翻阅航空发动机相关书籍。
有关工程流体力学基础的文章
- 详细阅读
-
控制体积法的分类与特性详细阅读
7.1.2 控制体积法的研究目的与方法1．研究目的研究流体流动问题时，如果使用积分控制体积法，其研究的目的主要是计算流体在研究区域表面或者控制体积内产生的质量变化率或者研究流体流动对研究区域造成的影响。......
2023-06-29
-
极小子流形体积的变分公式详细阅读
V（0）就是M的体积，可将V（t）视为Ft（M）的体积，因为当每个Ft都是整体等距嵌入时，V（t）的确是Ft（M）的体积．将公式（2．3．28）代入（2．3．25），有引理1（体积第一变分公式）因此，利用引理1，对任意的变分向量场W（x），体积的第一变分等于零的充要条件是x∈M，H（x）恒等于零．引理1给出了极小子流形的一个几何解释．另外，可以知道公式（2．3．29）和（2．3．30）给出了W（......
2023-11-23
-
微分控制体积法在流场数值模拟中的应用详细阅读
一般而言，研究重点放在流场内各点的压力、密度、温度与速度的变化，用到的微分控制方程包括质量微分守恒方程、动量守恒微分方程与能量微分守恒方程三种类型。质量守恒微分方程是标量，并不是向量。......
2023-06-29
-
使用推理公式法计算设计洪峰流量详细阅读
推理公式法是由暴雨资料推求小流域设计洪水的一种简化方法。所谓推理公式，也叫合理化公式，它是把流域的产流、汇流过程经过概化，利用等流时线原理推理得出小流域的设计洪峰流量的计算公式。G2.4.3.1推理公式的基本形式在一个小流域中，若流域的最大汇流长度为L，流域的汇流时间为τ。G2.4.3.2产、汇流参数的确定产流参数μ代表产流历时tc内地面平均入渗率，又称损失参数。推理公式法假定流域各点的损失相同，把μ视为常数。......
2023-06-21
-
结构图的等效变换和简化法详细阅读
为了便于分析和计算，需要将结构图中的一些方框基于“等效”的概念进行重新排列和整理，使复杂的结构图得以简化。图2-13n个方框串联的等效变换2.环节的并联传递函数分别为G1与G2的并联连接，如图2-14所示。其等效传递函数等于该两个传递函数的代数和。表2-1结构图简化的基本规则续表下面举例说明结构图的等效变换和简化过程。图2-17例2-7系统的结构图的化简例2-8 设系统的结构图如图2-18所示，试对其进行简化，并求闭环传递函数。......
2023-06-28
-
一个平凡公式的巧妙应用详细阅读
显然有△PBC+△PCA+△PAB＝△ABC，也就是图5-1这里h是△ABC的高。从式马上得到x+y+z＝h。这表明，不管P在△ABC内什么位置，它到三边距离之和，总等于△ABC的高。这个平凡公式的巧妙运用，会使他们兴致盎然地进入几何大花园。从这个公式出发，逻辑上会有一个很大的缺口。相比之下，我们宁可采用一条形式上较弱，叙述起来也较简单的命题：图5-3基本命题 如图5-3，设△ABC的AB边上有一点M。......
2023-10-17
-
水量平衡公式及其应用分析详细阅读
3.计算分区地表水量平衡公式城市计算分区(地表水):式中:CRWt、CLWt、CXWt分别为水库对城市供水量、城市当地可供水量以及外流域或区域对城市供水量;CDt、CIt、CAt、CEt、COt分别为城市生活用水、城市工业用水、城市农业用水、城市生态环境用水和城市其他用水;CETt、CFTt分别为城市蒸发、城市渗漏水量;CRWt为城市退水;CCWt为城市重复利用水量。......
2023-06-30
相关推荐