一个目标在上述约定下可以看成是n维空间中的一个向量,这就是向量空间模型的由来。下面结合目标的表示,给出其定义。,td};2)依据目标特征项序列,对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理,将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2025-09-29
在流体力学的问题研究中,除了使用直角坐标系,也常常会因为研究需要使用圆柱坐标系来研究流体流动。
6.6.1 直角坐标与圆柱坐标之间的关系
在直角坐标系上流体的流动性质与流体流速等物理量用流场内 x 轴、y 轴及 z 轴三个方向的分量来表示,而在圆柱坐标中流动物理量用流场内径向距离 r、方位角θ以及高度z三个参数的函数来表示。如图6-3 所示为圆柱与直角坐标之间的关系,从图中可以看出,直线![]() 的圆柱坐标与直角坐标之间距离关系可以用 x=r cosθ ; y=r sinθ 与z=z表示。在关系式中,x、y与z分别代表直角坐标上x轴、y轴与z轴的距离分量,而r、θ与z则分别代表圆柱坐标上的径向距离、方位角与高度。点P与点 Q 分别可以用圆柱坐标 P(r ,θ,z)和 Q(r ,θ,0)表示。
的圆柱坐标与直角坐标之间距离关系可以用 x=r cosθ ; y=r sinθ 与z=z表示。在关系式中,x、y与z分别代表直角坐标上x轴、y轴与z轴的距离分量,而r、θ与z则分别代表圆柱坐标上的径向距离、方位角与高度。点P与点 Q 分别可以用圆柱坐标 P(r ,θ,z)和 Q(r ,θ,0)表示。
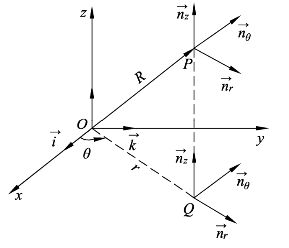
图6-3 圆柱坐标与直角坐标之间的关系
6.6.2 圆柱坐标的速度表示式

6.6.3 圆柱坐标的梯度运算符号定义
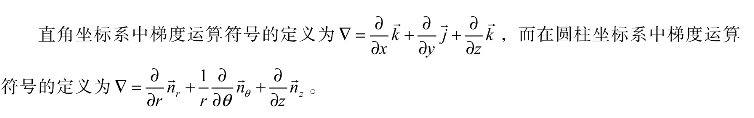
6.6.4 圆柱坐标中梯度运算符号与流速的点积计算式

6.6.5 圆柱坐标中梯度运算符号与流速的叉积计算式

6.6.6 圆柱坐标的对流时间导数计算式
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
【例6-6】
![]()
【解答】
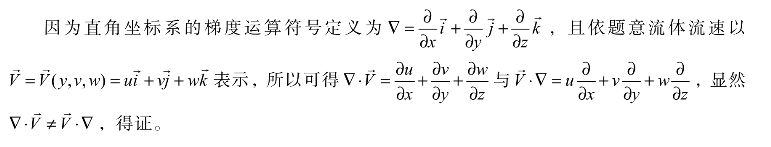
课后练习
(1)描述流体流动情况的主要物理量有哪些?
(2)系统、环境与边界的定义如何?
(3)控制质量系统与控制体积系统的定义如何?
(4)控制表面的定义如何?
(5)系统外延性质与内延性质的定义如何?
(6)描述流体流动的方法有哪些?
(7)为何在宏观流体力学中,拉格朗日法并不适用于流体流动参数的描述。
(8)列出流体加速度的计算公式并说明其公式中各项的物理意义。
(9)流体为稳态流动时,流体的对流加速度是否为0,其原因为何?

相关文章

一个目标在上述约定下可以看成是n维空间中的一个向量,这就是向量空间模型的由来。下面结合目标的表示,给出其定义。,td};2)依据目标特征项序列,对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理,将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2025-09-29

支持向量机是Vapnik及其合作者[130]根据结构风险最小化原则提出的一种在高维特征空间使用线性函数假设空间的学习系统。支持向量机是机器学习领域若干标准技术的集大成者。在若干挑战性的应用中,获得了目前为止最好的性能。,xn)′标记为正类,否则,将其标记为负类。图3-4 二维训练集的分开超平面(w,b)图3-5 最优超平面对于多个模式类的分类问题,输出域是Y={1,2,…......
2025-09-29

焊缝成分主要与焊接材料有关,当然也受熔合比和母材的影响。焊缝金属主要是在铸态条件下去满足使用要求的,一部分焊缝焊后经受热处理,而这些热处理又往往是简单的回火热处理,主要目的是去应力和软化。所谓焊接材料的成分是焊条、焊丝熔化后,完全没有母材参与的条件下所形成的焊缝金属的成分,没有熔合比的影响。熔合比是母材在焊缝中所占的比例。......
2025-09-29

图2-6 主应力状态图在一般情况下,变形毛坯内各质点的变形状态是不相同的。一点的应变状态可用一个平行六面体来表示,每个面上有一个正应变、两个切应变,共9个应变分量,经叠加刚性转动可使切应变互等,则仅有6个独立的应变分量。用主坐标系表示质点的应变状态,即单元体上仅有正应变,而无切应变;换言之,仅承受拉伸或压缩,而无角变形。图2-7 主应变状态图......
2025-09-29

上式中系数矩阵的各分块子阵分别为经过派克变换后的磁链方程为这就是变换到d、q、0坐标系统的磁链方程。式中的Ld和Lq分别是定子的等效绕组dd和qq的电感系数,称为直轴同步电感和交轴同步电感。在目前采用的变换矩阵情况下,磁链方程中互感系数不可互易问题,只要将各量改为标么值并适当选取基准值即可克服。则最终得到的磁链方程为习惯上常将d、q、0系统中的电势方程和磁链方程合称为同步电机的基本方程,亦称派克方程。......
2025-09-29

本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出时域分析时常用的MATLAB命令。例3-11 已知闭环系统传递函数为试用MATLAB判断系统的稳定性。图3-30例3-12系统的阶跃响应曲线图3-31例3-12系统的脉冲响应曲线例3-13 已知单位负反馈控制系统的开环传递函数为,试用MATLAB计算系统在单位阶跃信号作用下的tr、tp、ts、σ%。......
2025-09-29

主要介绍非圆柱沟槽凸轮传动和导丝动程自控两种成型机构及其差微的工作原理。非圆柱沟槽凸轮传动的工作原理如下:(一)非圆柱沟槽凸轮成型机构图7-8 所示为GD001 型络丝机成型机构,成型凸轮11 的回转通过嵌在凸轮内的转子12 使导丝托板13 往复运动,并使其上的角形导丝臂14 一起运动。当络丝筒子20 的卷绕半径增大时,承压辊19 使成型摇板15 随摇架17 绕支点O13顺时针方向摆动,导向杆16 就沿成型凸轮板13 上移。......
2025-09-29
相关推荐