一个目标在上述约定下可以看成是n维空间中的一个向量,这就是向量空间模型的由来。下面结合目标的表示,给出其定义。,td};2)依据目标特征项序列,对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理,将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2023-06-28
流体过程中通常有流体压力、温度、密度等性质以及速度、加速度和动量等物理量来描述流体状态与运动情况。其中压力、温度、密度属于标量,而速度、加速度和动量则属于向量。这里以直角坐标为例,针对标量与向量的定义、向量的大小、向量的计算以及梯度运算做主要说明。
6.3.1 标量的定义
所谓标量是指坐标变换下保持不变的物理量,也就是在使用不同的坐标系时,标量的值都相同,例如,在两个固定点之间的距离,不论从直角坐标系、圆柱坐标系或圆球坐标系来看,它的值都维持不变。因此标量(Scalar quantity)定义为只有大小而没有方向的物理量。
6.3.2 向量的定义
所谓向量(Vector)又称为矢量,它是指具有大小又有方向的物理量,例如位移、速率、加速度、力、力矩、动量、冲量等物理量,都是属于向量,向量存在的三要素为起点、大小与方向。向量同时具有大小与方向的双重属性,通常会在相应物理量上面加上箭号符号表示向量,例如的流动速度用符号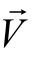 来表示,就是指研究流体流动的问题时,流速必须同时显示大小与方向,而如果用符号V来表示,就只表示它的大小,并不显示方向(本书为不妨碍理解,也部分保留 V 表示矢量速度)。有些书籍为了编辑方便,以粗体字表示向量,例如向量
来表示,就是指研究流体流动的问题时,流速必须同时显示大小与方向,而如果用符号V来表示,就只表示它的大小,并不显示方向(本书为不妨碍理解,也部分保留 V 表示矢量速度)。有些书籍为了编辑方便,以粗体字表示向量,例如向量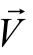 用符号V表示。
用符号V表示。
6.3.3 向量的表示法
6.3.4 向量大小的计算
6.3.5 向量的平行、相等与相反的定义
向量具有大小与方向的双重属性,因而在此描述与说明向量平行、相等与相反。
1.向量平行的定义
如果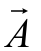 与
与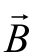 为两个非零向量,所指的方向相同或相反,则此两向量称为平行向量(Parallel vector),彼此不会相交。
为两个非零向量,所指的方向相同或相反,则此两向量称为平行向量(Parallel vector),彼此不会相交。
2.向量相等的定义
如果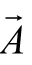 和
和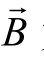 为两个非零向量,且大小与方向都相等,则此两向量称为相等向量(Equal vector),可以用数学式
为两个非零向量,且大小与方向都相等,则此两向量称为相等向量(Equal vector),可以用数学式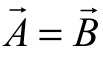 表示。
表示。
3.向量相反的定义
6.3.6 向量的计算
1.向量的加法计算
2.向量的减法计算
3.向量的点积计算
4.向量的叉积计算
两个向量的叉积计算可以用符号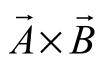 来表示,计算公式为
来表示,计算公式为
向量叉积得到的结果仍然为向量,也就是具有大小与方向的物理量,所以向量叉积(Vector cross product)又称为向量积(Vector product)。
6.3.7 梯度符号定义
有关工程流体力学基础的文章

一个目标在上述约定下可以看成是n维空间中的一个向量,这就是向量空间模型的由来。下面结合目标的表示,给出其定义。,td};2)依据目标特征项序列,对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理,将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2023-06-28

支持向量机是Vapnik及其合作者[130]根据结构风险最小化原则提出的一种在高维特征空间使用线性函数假设空间的学习系统。支持向量机是机器学习领域若干标准技术的集大成者。在若干挑战性的应用中,获得了目前为止最好的性能。,xn)′标记为正类,否则,将其标记为负类。图3-4 二维训练集的分开超平面(w,b)图3-5 最优超平面对于多个模式类的分类问题,输出域是Y={1,2,…......
2023-06-28

所有能定义在V上的线性泛函的集合,构成了一个与V采用同样标量集的向量空间,我们将它写作V*。事实上,在抽象代数意义上,V*和V是同构的。因此,我们称这些线性泛函为对偶向量或者余向量,称V*为对偶空间。构造对偶空间V*的对偶空间V(**),我们又会回到V,因此,V和V*就很像是彼此的镜像。每一个向量空间都有它的对偶空间,如果其中一个发生反变转换,那么另一个会发生共变转换,反之亦然。......
2023-11-22

张量积也是一个向量空间,但我们将这个向量空间里的向量称之为张量。张量积还解决了一个特殊的代数问题。它们的张量积VW构成了一个新向量空间,所用的也是同一组标量。参考阅读//No. 7 集合论,第18页No. 8 积,第20页No. 57 向量,第118页No. 76 维度,第156页右图:张量积可以把一个不完全的线性映射转化为一个线性映射。通过取张量积,我们可以将向量空间乘在一起,得到一个新向量空间。......
2023-11-22

,1)T.由于方程组的系数矩阵的n-1阶子式所以,方程组的系数矩阵的秩为n-1,从而α0是方程组的一个基础解系.因此λ=a+(n-1)b对应的所有特征向量为.设对应特征值λ=a-b的特征向量为y=(y1,y2,…......
2023-10-27

一、空间直角坐标系在空间,使3条具有相同单位长度的数轴相互垂直且相交于一点O,这3条数轴分别称为x轴、y轴和z轴,一般是把x轴和y轴放置在水平面上,z轴垂直于水平面.z轴的正向按如图7.1所示的右手法则判断,具体规定如下:伸出右手,让四指与大拇指垂直,并使四指先指向x轴的正向,然后让四指沿握拳方向旋转90°指向y轴的正向,这时大拇指所指的方向就是z轴的正向.这样就组成了右手空间直角坐标系Oxyz.......
2023-11-20

设A是n 阶矩阵,λ是一个数,若存在n维非零列向量ξ,使得则称λ是A 的特征值,ξ是A 的对应于特征值λ的特征向量.由①式,得ξ=0,因ξ≠0,故齐次方程组x=0有非零解,于是②式称为A 的特征方程,是未知量λ的n次方程,有n个根,λE-A称为特征矩阵,|λE-A|称为特征多项式.求出λi(i=1,2,…......
2023-11-21
相关推荐