直链淀粉含量与RVA谱的关系,因亚种的差异有所不一致。舒庆尧等对23个水稻品种的表观直链淀粉含量、RVA谱进行了研究,得出RVA谱的消减值和回复值与直链淀粉含量呈极显著正相关。Gravois等发现中等直链淀粉含量与RVA谱值的关系密切。......
2025-09-29
事实上,流体流动一定会有黏性。在流体流动过程中,黏性的存在会使得数学描述和处理变得十分困难。对于一些黏性较小的流体(例如水与空气等)或者黏性作用不占主导地位的流动问题,往往假设黏性μ=0来模拟真实的流体流动问题,例如第3章的内容中描述的稳态、一维与理想流体的处理方式就是最典型的。但是对某些黏性作用占据主导的问题,如果忽略流体黏性μ造成的影响,将会得到完全不符合实际情况的结果。例如本章前面的内容中提及的达朗贝尔悖论就是一个典型例子。
4.6.1 流体黏性的概念
物体在流体中运动时,流体会产生一个阻滞运动的力,此特有属性称为流体的黏性,而流体黏性产生的阻滞效应称为黏滞效应。流体黏滞效应与运动物体彼此之间好像物体在地面运动时,运动物体与地表面的摩擦效应及其彼此之间的关系。研究指出,流体的黏性主要受流体分子与分子之间的吸引力(流体的内聚力)以及流体分子的运动力等因素影响。其中流体的内聚力为影响液体黏性的主要因素,而流体分子的运动力为影响气体黏性的主要因素。又根据实验发现,流体的黏性受温度的影响很大,对于液体而言,液体内部分子与分子之间的吸引力,也就是液体内部的内聚力是影响液体黏性的主要因素:温度升高时,液体会逐渐地蒸发为气体,液体内部的内聚力会逐渐减少,液体的黏性减少;温度降低时,液体的黏性增加。对于气体而言,气体内部分子的运动力是影响气体黏性的主要因素,且依据气体分子动力理论,当气体温度升高,气体内部的动能增加,内部分子的运动也随之增加。因此温度升高时,气体黏性增加;温度降低时,气体黏性减少。由此可知液体的黏性与气体的黏性受温度增减影响的反应趋势相反。此外,实验还证明,流体的黏性受压力的影响通常不大,一般在工程计算中不予以考虑。
4.6.2 无滑流现象
流体因为具有黏性,在流经物体表面时,流体分子与物体接触表面会受彼此之间的相互作用,在接触表面达到动量的平衡,因此流体速度会和接触表面的相同,此现象即为无滑流现象(No-slipping condition)。同理,物体表面流体分子达到能量的平衡,流体温度会和接触物体表面的相同,此现象即为无温度跳动现象(No temperature jump condition)。在流体力学与空气动力学问题研究中,无滑流现象与无温度跳动现象主要当成黏性流体在接触表面速度与温度的边界条件。
4.6.3 牛顿流体的意义
除非特别说明,流体一般都当成牛顿流体来处理,气体自然也不例外。所谓牛顿流体(Newtonian fluid)是指定温及定压下,流体受到的剪应力与流体速度梯度成正比,也就是满足牛顿黏性定律公式![]() 的流体。式中,τ是流体受到的剪应力(Shear stress),定义为流体在单位面积上受到的黏滞力,μ为流体的动力黏性系数(Dynamic viscosity coefficient),它是流体受到的剪应力τ与速度梯度
的流体。式中,τ是流体受到的剪应力(Shear stress),定义为流体在单位面积上受到的黏滞力,μ为流体的动力黏性系数(Dynamic viscosity coefficient),它是流体受到的剪应力τ与速度梯度![]() 的比例常数。流体的黏性一般用动力黏性系数表示,又称为流体的黏度(Viscosity)或动力黏度(Dynamic viscosity),其与流体种类与温度有关。许多空气动力学问题研究中,惯性力总是和黏性力同时并存的,流体的黏度μ和密度ρ的比值起着重要作用。有时用它们的比值来表示气体的黏性更为方便,因此,定义
的比例常数。流体的黏性一般用动力黏性系数表示,又称为流体的黏度(Viscosity)或动力黏度(Dynamic viscosity),其与流体种类与温度有关。许多空气动力学问题研究中,惯性力总是和黏性力同时并存的,流体的黏度μ和密度ρ的比值起着重要作用。有时用它们的比值来表示气体的黏性更为方便,因此,定义 式中ν即称为流体的运动黏性系数(Kinematic viscosity coefficient)或流体的运动黏度(Kinematic viscosity)。
式中ν即称为流体的运动黏性系数(Kinematic viscosity coefficient)或流体的运动黏度(Kinematic viscosity)。
4.6.4 边界层的概念
边界层(Boundary layer)的概念是指液体与气体流经物体表面时,液体与气体在物体表面附近的流场会形成所谓的边界层,虽然它是一个假想的概念,但在流体力学与空气动力学问题研究中却是一个非常有用且不可或缺的处理模式。边界层(Boundary layer)的概念在2025年由普朗特提出。对于雷诺数较大的黏性流体流动可以将其看成由两种不同形态的流动组成:一种是固体边界(接触物体表面)附近流场的流动,也就是边界层内流体的流动,此时黏性产生的黏滞作用不可忽略,也就是必须把流体视为黏性流体;另一种是指边界层以外的流体流动,此时,流体黏性产生的黏滞效应可以忽略不计,也就是可以将边界层外的流动流体视为无(非)黏性流体。这种处理黏性流体流动的方法为近代流体力学的发展开辟了新的途径。这里针对边界层的定义、现象与使用时机等部分简单地描述,至于气体在高于声速流动时的激波与边界层的相互干扰问题,过于复杂,不属于本书的讨论范围。
1.概念说明
如图4-2 所示,以空气流经平板为例,虚线代表边界层,在边界层的内部必须考虑空气流场的黏性,而在边界层的外部,则将空气流场的黏性忽略不计。除此之外,空气与平板形成的边界层会随空气流经平板的距离而逐渐增厚,这是因为空气流经平板的距离(x方向)越长,空气受到黏性影响越大的缘故。
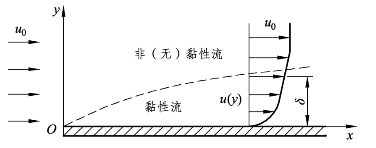
图4-2 边界层概念
2.边界层厚度的定义
为了区分黏性流区域与非(无)黏性流区,必须先了解边界层厚度(Boundary layer thickness)的定义,仍以流体流经平板的外部流动来说明。如图4-3 所示为均匀流体以等速度u0流经平板的速度变化。流体在边界层内的流体的流速为u(y),y为流体质点与固定表面的垂直距离。如果边界层内流体的流速达到 99% u0,在y轴的位置δ,可以假设其以外的区域为非黏性流区,则δ即为边界层的厚度。由于流体不受流体黏性影响的速度为自由流速度u0,所以边界层厚度的定义可以表示为 u (δ)=0.99u0。一般而言,固定表面的垂直距离y大于或等于边界层厚度δ时,假设流体的流速不会受到流体黏性影响,即假设 u(δ)=u0。边界层厚度的定义和前面提及的无滑流现象一样,在流体力学与空气动力学问题研究中,主要当成是黏性流体流速的边界条件之一。

图4-3 边界层厚度定义的示意图
又从图4-3 中可以发现,流体流动会因为边界层效应的影响造成外围流线的微小位移δ,称之为位移厚度(Displace thickness)。由于边界层非常细薄,也就是边界层的厚度非常小,流体流动受边界层效应产生的流线位移,也就是位移厚度影响可以忽略不计。
3.不适用情况
对于雷诺数 Re 很小的流场,黏性流区与无黏性流区之间的相互作用相当强烈,而且其间的变化趋势是非线性的,所以如果流场的雷诺数非常小,边界层理论可能并不适用。而在气体发生流体分离时,气体回流现象会产生,边界层理论也不适用。
【例4-10】
如图4-4 所示,U0为均匀气流的速度,u(y)为边界层内气流的速度分布,δ为边界层的厚度,问u(0)与u(δ)的值是多少?
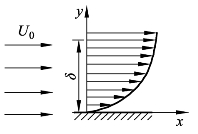
图4-4 边界层气流速度分布
【解答】
(1)由于无滑流现象,因此与固定平板接触的流体分子的速度u(0)=0。
(2)根据边界层厚度的定义,u (δ)=0.99U0,通常为简化问题,一般采用 u(δ)=U0。(https://www.chuimin.cn)
4.6.5 流体分离的概念
流体分离是黏性问题研究的一个重要课题,例如飞机在亚声速飞行时,气体分离现象会引起飞机飞行升力急速下降,导致飞机失速而造成飞行事故。
1.正负压力梯度的概念
如第3章所述,空气流经物体曲面,例如机翼翼型的上表面时,从其前缘开始,气流的流管逐渐变细,流速逐渐加快,压力会逐渐地减小,其压力变化的趋势是负压力梯度![]() 当到达某一点E时,气流的流管最细,气流的流速最快,此时气流的压力梯度为0。当气流流经E点后,随着气流继续向后流动,气流的流管又逐渐地变粗,流速逐渐减慢,压力逐渐地增大,其压力变化的趋势将转为正压力梯度
当到达某一点E时,气流的流管最细,气流的流速最快,此时气流的压力梯度为0。当气流流经E点后,随着气流继续向后流动,气流的流管又逐渐地变粗,流速逐渐减慢,压力逐渐地增大,其压力变化的趋势将转为正压力梯度![]() 如图4-5所示。
如图4-5所示。
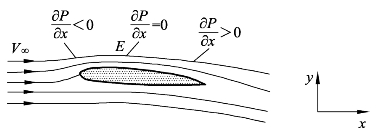
图4-5 流经机翼翼型上表面气流压力变化
从以上例子可以知道,空气流经机翼翼型的上表面时,气流先加速后减速,因此会有速度梯度与压力梯度。当机翼后缘的正压力梯度到达某一特定值时,流体分离的现象就会产生并导致失速的发生。
2.流体分离的定义
所谓流体分离(Flow separation)是指沿着物体表面边界层内的气流由于黏性的作用消耗了动能,在压力沿着流动方向增高的区域中,无法继续沿着物体表面流动,以致产生气体倒(回)流的现象,气流因而离开物体表面。如图4-6 所示为气体流经平板问题的示意图,边界层的厚度非常小,流体流动因为边界层效应影响造成外围流线的微小位移通常可以忽略不计,因此气体流经平板时压力沿着流动方向几乎保持不变,即![]() 当气体流经平板时一般不会有流体分离的现象发生,只有在气体流经弯曲壁面时才可能会发生流体分离。
当气体流经平板时一般不会有流体分离的现象发生,只有在气体流经弯曲壁面时才可能会发生流体分离。
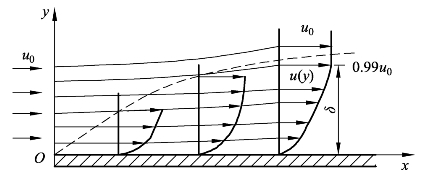
图4-6 气体流经平板问题
3.现象描述
如图4-7 所示,气流沿着弯曲壁面流动,在弯曲壁面前方的自由流(Free flow),也就是未受黏性效应影响的气流,即无黏性流的流速U沿着弯曲壁面因为气流的流管逐渐变细而逐渐加速,一直到B点时才会停止加速。当气流到达B点后继续流动,气体流速会因为气流的流管逐渐变粗逐渐减速。由此可以推知,在B点之前的压力变化趋势是负压力梯度,也就是![]() 而B点之后的压力变化趋势是正压力梯度,也就是
而B点之后的压力变化趋势是正压力梯度,也就是![]() 至于B点时的压力梯度为0即
至于B点时的压力梯度为0即![]() 且该点的气体流速最大。当气体气流到达B点后继续沿着弯曲壁面流动时,气流的正压力梯度会逐渐地增加,当达到某一特定值时,气体将因为前方的压力过大而逐渐地无法再继续流动,开始发生气流回流的现象,所以沿着物体表面边界层内的气流会发生流体分离,如图4-7中的D点与E点所示。
且该点的气体流速最大。当气体气流到达B点后继续沿着弯曲壁面流动时,气流的正压力梯度会逐渐地增加,当达到某一特定值时,气体将因为前方的压力过大而逐渐地无法再继续流动,开始发生气流回流的现象,所以沿着物体表面边界层内的气流会发生流体分离,如图4-7中的D点与E点所示。
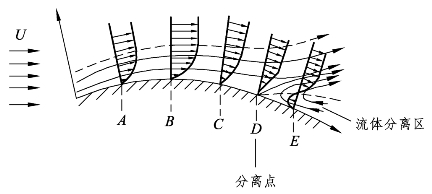
图4-7 流体分离的示意图
4.现象分析
将流体分离现象归纳成一个简单的规律,就是负压力梯度![]() 与零压力梯度
与零压力梯度![]() 不会发生流体分离,只有正压力梯度
不会发生流体分离,只有正压力梯度![]() 才有可能发生流体分离的现象。但是微小的正压力梯度并不会直接产生流体分离,只有气流的正压力梯度大到一定程度时才有可能会发生流体分离,如图4-8所示。
才有可能发生流体分离的现象。但是微小的正压力梯度并不会直接产生流体分离,只有气流的正压力梯度大到一定程度时才有可能会发生流体分离,如图4-8所示。
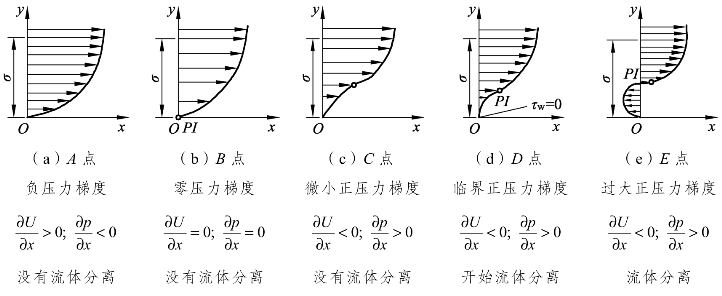
图4-8 流体分离现象分析
从图4-7 与图4-8 中可以看出,A 点与 B 点由于压力梯度![]() 小于等于0,所以不会发生流体分离,C 点虽然压力梯度大于0,但是正压力梯度
小于等于0,所以不会发生流体分离,C 点虽然压力梯度大于0,但是正压力梯度![]() 过小,所以也不会发生流体分离。气体沿着弯曲壁面继续流动,随着正压力梯度
过小,所以也不会发生流体分离。气体沿着弯曲壁面继续流动,随着正压力梯度![]() 逐渐地增加,当气体流至曲面 D 点时,气流的流场开始产生流体分离,D 点的压力梯度则称为临界正压力梯度(Critical positive pressure gradient),而 D 点即称为分离点(Separation point)。根据流体分离的定义,D点的壁面剪应力为0(τw=0)。如果气流继续再沿着弯曲壁面推进,气体会因为前方的压力过大而逐渐地无法再继续流动,开始发生气流回流(Airflow reflux)的现象,如图4-7与图4-8的E点所示。实验证明气流流动时正压力梯度和气体黏性是气体产生分离的根本原因。湍流流场因为边界层内流体的平均动量大,在相同正压力梯度情况下向前推进的能力较强,因此其分离点会比层流流场分离点稍微靠后一些,这也是高尔夫球为何要做成凹凸不平的原因。
逐渐地增加,当气体流至曲面 D 点时,气流的流场开始产生流体分离,D 点的压力梯度则称为临界正压力梯度(Critical positive pressure gradient),而 D 点即称为分离点(Separation point)。根据流体分离的定义,D点的壁面剪应力为0(τw=0)。如果气流继续再沿着弯曲壁面推进,气体会因为前方的压力过大而逐渐地无法再继续流动,开始发生气流回流(Airflow reflux)的现象,如图4-7与图4-8的E点所示。实验证明气流流动时正压力梯度和气体黏性是气体产生分离的根本原因。湍流流场因为边界层内流体的平均动量大,在相同正压力梯度情况下向前推进的能力较强,因此其分离点会比层流流场分离点稍微靠后一些,这也是高尔夫球为何要做成凹凸不平的原因。
【例4-11】
如图4-9 所示,O 点为分离点(边界层内的气流开始发生分离现象的临界点),u(y)为边界层内气流的速度分布情形,δ为边界层的厚度,假设物体为静止状态,问在物体表面(y=0),O点的 u(δ)、 u(0)与![]() 是多少?
是多少?
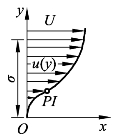
图4-9 分离点处边界层过渡分布
【解答】
(1)根据边界层厚度的定义,并通常为简化问题起见,采用u(δ)=U。根据无滑流条件,与表面接触的气体分子和接触物体表面有相同的速度,所以u(0)=0。
(2)根据分离点存在条件,流体分离的临界情况出现在壁面剪应力等于0的位置,因此壁面(y=0)时的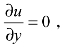 也就是
也就是 。
。
相关文章

直链淀粉含量与RVA谱的关系,因亚种的差异有所不一致。舒庆尧等对23个水稻品种的表观直链淀粉含量、RVA谱进行了研究,得出RVA谱的消减值和回复值与直链淀粉含量呈极显著正相关。Gravois等发现中等直链淀粉含量与RVA谱值的关系密切。......
2025-09-29

采用分子混沌假设,并认为颗粒之间以二体碰撞为主。上述本构关系式由Gidaspow 针对气固两相流率先提出,在气固两相流模拟中获得了较广泛的应用。因此,上述本构关系严格地说,仅适用于速度梯度较小、颗粒近乎弹性的颗粒流。......
2025-09-29

在渗透变形试验的前期,渗透系数随水力梯度的增加变化幅度不大,基本保持不变。表5.6给出了渗透变形试验规程和本书建议的方法得到的临界水力梯度对比。由表5.6可知,含黏粗粒土试样即使在应力较低的情况下,其渗透变形的临界水力梯度也较“零附加应力”状态下的试件临界水力梯度高出许多。......
2025-09-29

图2.17活性射流成形过程中温度分布数值模拟结果活性药型罩顶部轴线处微元温度随时间的变化如图2.18所示。图2.20活性药型罩底部微元温度随时间的变化从机理上分析,在爆炸驱动作用下,活性药型罩材料温升需要一定时间才能导致活性材料聚合物基体发生分解,释放足够多氧化剂后,活性金属粉体才能与氧化剂发生剧烈的化学反应。......
2025-09-29

淀粉分支酶又称Q酶,在支链淀粉结构形成中有重要的作用。根据淀粉分支酶作用的底物和形成的分支链长,可将同工型分为SBEI和SBEII两个家族。A型的突变体中,直链淀粉含量高,支链淀粉分支减少且分支链增长。Chrastil等认为,淀粉分支酶变化动态与支链淀粉聚合度、链的长度、链数有关,而这些结构都与稻米食味品质紧密相关。......
2025-09-29

得出气缸内气体压力和容积数据,并把此数据显示在对数-对数坐标中,可以得出压缩行程和膨胀行程中的多变指数。另外,CI发动机在膨胀过程期间n值为1.0、1.3、1.35持续增加,这表示在膨胀过程期间持续发生燃烧。其次,要看一下多变指数n与工质供给热量δQ之间的关系。膨胀多变指数ne在膨胀冲程初期变小,但在持续燃烧作用下逐步增大,直到燃烧结束后保持一定。......
2025-09-29

直链淀粉含量、胶稠度和糊化温度,是衡量稻米蒸煮加工和食用品质优劣的三项理化指标。稻米中直链淀粉含量高,糊化温度升高,胶稠度降低,使饭质变硬、口感差。在全部57个B3F5代株系中,直链淀粉含量和胶稠度与Wx基因型同步分离,表明直链淀粉含量主要由Wx基因控制,胶稠度也由Wx基因或与其紧密连锁的基因位点控制。......
2025-09-29

对于绝大多数板料,均可满足这两个要求,但各种材料冲裁后,所得的制件质量与模具的磨损程度相差很大。塑性较好的板料在冲裁后,通常需要进行整修和去毛刺,塑性差的材料或厚板料冲裁时,为了提高板材的塑性,可采取加热方法,如冲裁有机玻璃时一般都需要加热到60℃左右后才冲裁。......
2025-09-29
相关推荐