等熵过程中的气体压力与温度不变性

2023-06-29 理论教育版权反馈

【摘要】：在等熵过程中，没有能量损耗与热功交换，因此气体的总压 tP与总温tT一定会分别保持在一个固定常数值。对于工程精度要求较高的计算问题，等熵过程假设可能不再适用，必须视实际情况对计算公式加以修正。式中，P1与 P2、T1与T2以及 ρ1与 ρ2分别表示等熵过程中状态1与状态2的压力、温度与密度。

一般而言，在研究气体的弱扰动过程（Weak disturbance process）或者高速气体在管道内的流动问题时，通常将气体状态改变的过程视为一个等熵过程并配合理想气体方程式P=ρRT加以计算。

4.3.1 相关过程定义

所谓等熵过程（Isentropic process）又称为可逆绝热过程（Reversible adiabatic process），它是指过程在进行时必须同时满足可逆过程（Reversible process）与绝热过程（Adiabatic process）的成立条件。

1．可逆过程的定义

可逆过程是指一个过程如果发生后，系统与外界环境两者都能够以任何的方式，依照能量守恒的原则，回到过程进行前的状态，则该过程称为可逆过程。倘若一个过程不是可逆的，就称为不可逆过程（Irreversible process），不可逆过程在过程发生时一定会造成能量的损耗。研究指出，一个过程如果要满足可逆，必须同时满足（1）无摩擦；（2）温度差无限小和传热无限慢；（3）压力差无限小和作用力无限小；（4）无自发性反应；（5）无化学反应；（6）所有的变形完全都是弹性变形；（7）无磁滞作用。但事实上，气体的流动过程一定会有摩擦或黏滞效应，而能量转换的过程，也不可能没有温度差以及压力差，所以实际工程应用中，气体的流动过程不可能是可逆的，一定会产生能量的损耗。在工程设计的观点中，虽然可逆过程不可能实现，但是就从理论上来看，可逆过程不会产生能量损耗，所以理论上的效率是最高的。在热力工程、流力工程与空气动力学问题的工程计算中，总是引用可逆过程的概念来找出理想效率，将其当成改进实际过程的一个标准和努力的方向，并识别出可能造成不可逆的各种实际因素，判别不利影响，从而提出最合理的工程方案。

2．绝热过程的定义

绝热过程是指一个过程如果进行时，系统与外界环境没有热量的交换，则该过程称为绝热过程（Adiabatic process），倘若一个过程不是绝热的，则该过程称为非绝热过程（Non-adiabatic process）。事实上，过程进行的时候只要与外界的环境之间有温度的差异就会有热量的传递，所以绝热和可逆一样只是理想的假想过程。不过在工程计算中往往会使用此假设来简化问题研究的难度，例如管道内高速流动的气体，气流与管壁接触的时间很短，在流经管道时造成的热量损失占整个系统内能量损失的比例非常小，则在工程计算时可以将热量的散失量忽略不计，也就是将该过程视为绝热过程来简化工程计算的难度。

3．等熵过程的定义

等熵过程又称为可逆绝热过程，是指过程进行时必须同时满足可逆过程与绝热过程的成立条件，其被定义为“如果一个过程在进行时，系统与外界没有热量交换，而且在进行后，系统与外界两者之间能够以任何的方式，依照能量守恒的原则，回到过程进行前的状态，则该过程就称为等熵过程”。在等熵过程中，没有能量损耗与热功交换，因此气体的总压 tP与总温tT一定会分别保持在一个固定常数值。高速气流在流动的过程中，其压力P、密度ρ与温度T等流动性质变化相当复杂，必须使用许多假设条件对问题进行简化。对于气体的弱扰动过程或者中高亚声速气流，通常使用等熵过程假设找出气体流动的规律或做粗略的估算。对于工程精度要求较高的计算问题，等熵过程假设可能不再适用，必须视实际情况对计算公式加以修正。

4.3.2 计算公式

研究发现，气体在等熵过程，也就是可逆绝热的过程中，其压力（P）与密度（ρ）之间的关系可以使用计算公式P=Cγρ来描述，此计算公式为等熵方程。式中，P与ρ分别表示气体的压力与密度，γ为等熵指数，其值等于1.33～1.4，而C为某一个特定的常数。

4.3.3 压力、温度与密度变化的关系

根据等熵方程式P=Cγρ与理想气体的状态方程式P=ρRT，可以得到等熵过程中压力、温度与密度的计算关系式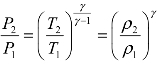 pagenumber_ebook=88,pagenumber_book=81 。式中，P1与 P2、T1与T2以及 ρ1与 ρ2分别表示等熵过程中状态1与状态2的压力、温度与密度。

4.3.4 停滞参数的定义及其与马赫数之间的关系

所谓气体的停滞参数（Stagnation parameter）是探讨稳态一维流场时，气体处于停滞状态的气流参数，也就是研究稳态一维的流场中气体流速为零的状态参数，一般也将停滞参数称为总参数（Total parameter）。流体力学与空气动力学问题研究过程中，关于停滞参数或总参数方面的研究重点通常放在气流为等熵流动时，气体的停滞温度、停滞压力与停滞密度三个主要的状态参数，而在工程实践中使用最多的主要是探讨等熵流动时，气体停滞参数与气流马赫数的关系。

1．停滞温度

pagenumber_ebook=88,pagenumber_book=81

2．停滞压力

pagenumber_ebook=89,pagenumber_book=82

3．停滞密度

pagenumber_ebook=89,pagenumber_book=82

4．停滞参数的变化规律

pagenumber_ebook=89,pagenumber_book=82

【例4-5】

如图4-1所示，如果气体的流动视为可逆绝热过程，而驻点A的温度为40 °C，气体的温度为 15 °C，试求气流Ma、速度V以及停滞压力 Pt和气流压力P的比值，这里等熵指数γ的值定为1.4。

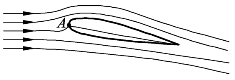
pagenumber_ebook=89,pagenumber_book=82

图4-1 翼型浇流

【解答】

（1）所谓驻点A的温度就是指气流的停滞温度（总温）Tt，必须注意的是气体在等熵流动过程中，气流的停滞温度tT和气流的温度与气流Ma之间的关系式必须使用绝对温度。

pagenumber_ebook=90,pagenumber_book=83

5．压力、温度以及密度和马赫数的关系

pagenumber_ebook=90,pagenumber_book=83

6．适用条件

使用等熵假设求出气体的流动性质变化的规律，对于工程精度要求不高的问题，计算结果通常可以直接使用，但是对于工程精度要求较高的问题，等熵过程的假设可能就不再适用，必须视实际情况对计算公式加以修正。此外，气体弱扰动问题的研究过程中，由于气体性质变化量非常小，通常可以将气体流动的过程当成可逆绝热，也就是以等熵形式来处理。但是如果是研究气体的强压缩过程，例如正激波与强斜激波，气体性质变化剧烈，此时只能够将其假设为绝热过程。

【例4-6】

假设空气在管道等熵可压缩流动，等熵指数γ=1.4，在管道进口 M1=0.3，截面积A1=0.001 m2，温度T1=62 °C 与绝对压力P1=650 kPa 。而在管道出口 M2=0.8，试求管道出口处的温度T2与绝对压力 P2的值。

【解答】

pagenumber_ebook=91,pagenumber_book=84