伯努利方程是能量守恒定律在流动液体中的表现形式。因而液体AB 段在Δt 时间流动时动能变化为:根据动能定理,外力所做功的总和等于液体能量的增量,即故有:将上式两边分别除以Δmg,整理得:或式和式称为理想液体的能量方程,一般称为理想液体的伯努利方程。式称为实际液体的伯努利方程。......
2023-06-18
伯努利方程用于研究、设计与计算低速流体流动的问题时,通常计算结果和实际测量压力与速度值彼此之间的误差不大,但是对于某些时刻或精确度要求较高的工程问题研究方程必须做修正。最常讨论的有动能修正系数、流体黏性损失等。
3.4.1 动能修正系数

3.4.2 流体黏性损失


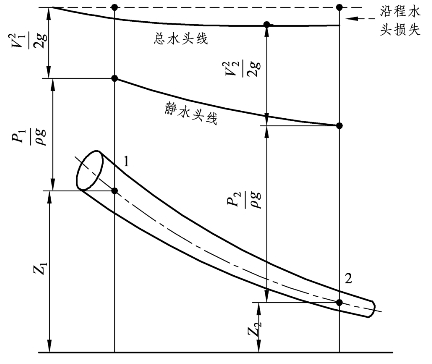
图3-14 沿程水头损失
低速流体流经工业管道时,由流体的黏性效应与管壁粗糙度引起的表面阻力导致的能量损失为所有能量损失的主要部分,因此流体黏性损失又称为摩擦损失(Friction loss)、表面阻力损失(Surface drag loss)或者主要损失(Major loss)。
【例3-6】
某新铸铁管管壁的粗糙度为 0.3 mm,长 L= 100 m ,管径 D= 0.25 m ,水温为20 °C,水流量 Q= 0.05 m3/s ,沿程阻力系数 f= 0.021,求流体的流速V与沿程水头损失hf。
【解答】
根据体流率守恒公式![]() ,可得流体的流速 V= 1.019 m/s 。沿程水头损失为hf=0.455 m (水柱)。
,可得流体的流速 V= 1.019 m/s 。沿程水头损失为hf=0.455 m (水柱)。
3.4.3 局部阻力损失
所谓流体的局部阻力损失(Local drag loss)是指流体在工业管道中流经各种局部障碍装置,例如变径管、弯管与阀门时,由于管路上不同形状配件或管路本身的弯曲或变形引起的局部能量损失。流体的局部阻力损失又称为形状阻力损失(Shape drag loss),而单位质量流体的局部阻力损失则称为局部水头损失(Local head loss)。工程实践发现,低速流体流经工业管道时,流体流过局部障碍装置造成的能量损失与流体黏性损失相比较小,所以流体的局部阻力损失又称为微量损失(Micro loss)或者次要损失(Minor loss),其能量损耗示意图如图3-15 所示。计算公式为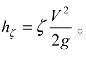 式中,hζ为局部水头损失或形状损耗落差(Shape loss drop);ζ为局部阻力系数(Local drag coefficient)或形状损耗落差系数(Shape loss drop factor),它的大小与流体的雷诺数Re和局部障碍的结构形式有关;V 为流体流经管道截面的平均流速,通常是指流体流经局部障碍之后的流速;而g为重力加速度,其值为9.81 m/s2。
式中,hζ为局部水头损失或形状损耗落差(Shape loss drop);ζ为局部阻力系数(Local drag coefficient)或形状损耗落差系数(Shape loss drop factor),它的大小与流体的雷诺数Re和局部障碍的结构形式有关;V 为流体流经管道截面的平均流速,通常是指流体流经局部障碍之后的流速;而g为重力加速度,其值为9.81 m/s2。
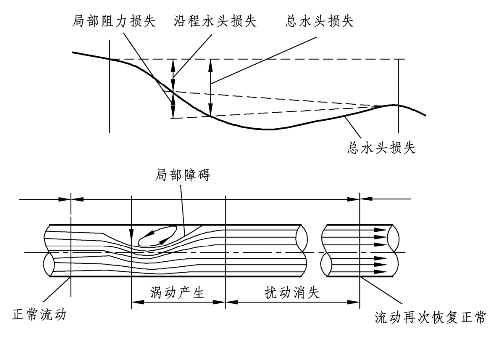
图3-15 流体流经管道的能量损耗
流体流经工业管道时造成局部阻力损失或形状阻力损失的原因大抵能够分成五类描述如下。
(1)由于管道截面面积发生变化引起的损失。
流体流经工业管道时会因为管道截面面积发生变化而引起局部的能量损失,例如突缩、突扩、渐缩、渐扩管流。
(2)由于管道的方向发生变化引起的损失。流体流经工业管道时会因为管道的方向发生变化而引起局部能量损失,例如流体流经弯管或折管时会造成流体的局部能量产生损耗。
(3)由于在管路中设置控制流量装置引起的损失。例如在管路中设置控制各种阀门或开关,当流体流过这些装置时,流体流速的大小与方向会受到影响,因此造成流体的局部能量损耗。
(4)由于在管路中设置分流及合流装置引起的损失。例如在管路中装设 Y 形管、T形管、十字形管与三通管等装置,当流体流过这些装置时,流体流速的大小与方向均会受到影响,流体的局部能量产生损耗。
(5)由于在管路中装设测量仪器引起的损失。例如在管路中装设流速仪、流量计、压力计与温度计等测量仪器,当流体流过这些仪器时,流体流速的大小与方向均会受到影响,流体的局部能量产生损耗。
当考虑流体的局部阻力损失时,理想流体的伯努利方程应该修正为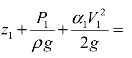
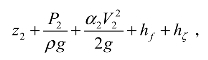 式中hf与hζ分别为沿程水头损失与局部水头损失。实际上,低速流体管道流动会受到流体黏性损失与局部阻力损失的影响,流体的机械能会逐渐减小,造成总水头线逐渐降低,如图3-15 所示。局部阻力系数ζ的大小与流体的雷诺数Re和局部障碍的结构形式有关,除个别简单情况可以理论求得外,其他大多数只能由实验加以确定。虽然局部障碍装置有多种形式,引起局部阻力的特性和大小各异,但这些局部阻力的共同特点是集中在一段较短的流程内,因此为方便起见,工程问题研究通常将局部阻力损失看作集中在管路中一点加以计算。
式中hf与hζ分别为沿程水头损失与局部水头损失。实际上,低速流体管道流动会受到流体黏性损失与局部阻力损失的影响,流体的机械能会逐渐减小,造成总水头线逐渐降低,如图3-15 所示。局部阻力系数ζ的大小与流体的雷诺数Re和局部障碍的结构形式有关,除个别简单情况可以理论求得外,其他大多数只能由实验加以确定。虽然局部障碍装置有多种形式,引起局部阻力的特性和大小各异,但这些局部阻力的共同特点是集中在一段较短的流程内,因此为方便起见,工程问题研究通常将局部阻力损失看作集中在管路中一点加以计算。
3.4.4 总能量损失
流体流经工业管道时总是同时产生流体黏性损失与局部阻力损失,于是某段管道流体产生总能量的损失应该是这段管路上各种能量损失的迭加,因此总水头损失应该是在这段管路的沿程水头损失hf与局部水头损失hζ的迭加,即 htotal=∑ hf+∑ hζ。
3.4.5 综合归纳
1.使用时机
一般而言,对于低速流体在工业管道流动时,通常用理想流体的伯努利方程式来计算流体流速与压力的关系。但对于精确度要求较高的工程计算或问题研究需要,可能必须考虑动能计算误差或流体黏性损失和局部阻力损失造成的能量损耗计算误差。
2.计算公式

3.物理现象

4.注意事项
低速流体流经工业管道时,流体的局部阻力损失与流体的黏性损失相比较小,所以在要考虑流体的局部阻力损失时,必须考虑流体的黏性损失。此外在研究低速管流问题时,可依实际需求将伯努利修正方程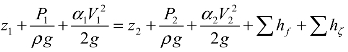 适时简化,也就是将动能计算误差或能量损耗计算误差适时予以忽略,简化工程计算的难度,以期在满足精度要求的情况下,用最少的工作时间与计算成本完成研究任务。
适时简化,也就是将动能计算误差或能量损耗计算误差适时予以忽略,简化工程计算的难度,以期在满足精度要求的情况下,用最少的工作时间与计算成本完成研究任务。
课后练习
(1)处理低速流体流动时常用的假设有哪些?
(2)不可压缩流体的假设与使用时机是什么?
(3)不可压缩流体与可压缩流体的判定准则是什么?
(4)非黏滞性流体的假设与使用时机是什么?
(5)什么是理想流体?什么是不可压流体? 什么是非黏滞性流体?运用条件各有什么特点?
(6)理想流体的假设与使用时机是什么?
(7)质量流率的物理意义与计算公式是什么?
(8)体积流率的物理意义与计算公式是什么?
(9)质量流率与体积流率两者的区别与联系是什么?
(10)质量流率守恒公式的物理意义、使用假设与计算公式是什么?
(11)体积流率守恒公式的物理意义、使用假设与计算公式是什么?
(12)低速稳定流体流经单一进出口的流管,流体截面的质量流率与体积流率的关系是什么?
(13)平均流速的物理意义与计算公式是什么?
(14)伯努利方程式的物理意义、使用假设与计算公式是什么?
(15)空速计的设计原理是什么?
(16)空速计的计算公式是什么?
(17)如果棒球是顺时针方向向右投出旋转,那么棒球将会是上飘还是下坠?
(18)如图3-16 所示,假设空气流动时的密度变化量忽略不计,试求速度1V与V2之间的关系。
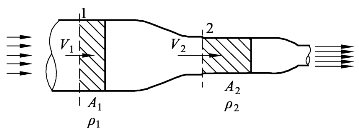
图3-16 变截面管道流动
(19)如图3-17所示,低速流体在流管内压力与速度随着面积变化的关系是什么?

图3-17 管道流动
(20)如图3-18所示,问空气流速与液柱的关系式是什么?
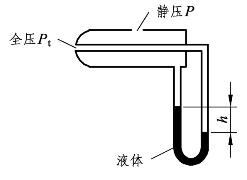
图3-18 压差计
(21)如图3-19 所示,三段管路串联,已知直径 d1=1 mm,d2=0.5 m,d3=0.25 m ,截面平均速度 V3=10 m/s ,请问V1和V2的速度大小是多少?
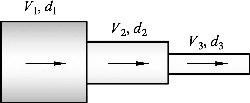
图3-19 三段管路流动
(22)两船靠近并行,可能会产生什么危险?为什么?
(23)如果喷嘴的管件如图3-20所示,流体比重 S为0.85的油经喷嘴射出,截面1的直径 d1=10 cm ,截面2的直径 d2=4 cm ,U形压差计测量出的压力差为7×105 Pa,求单位时间流经喷嘴管件截面的流量。
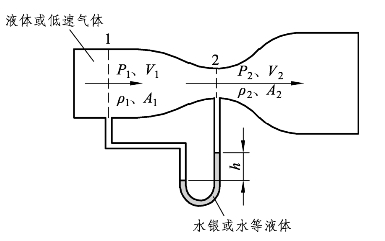
图3-20 流量计
(24)造成沿程水头损失hf的原因是什么?其计算公式又是什么?
(25)影响沿程水头损失hf的因素是什么?
(26)影响沿程阻力系数或者摩擦损耗落差系数的因素是什么?
(27)造成局部水头损失hζ的原因是什么?其计算公式又是什么?
(28)影响局部水头损失hζ的因素是什么?
(29)对于低速流体在同一管道的流动问题,可能导致流动能量损失的因素是什么?
(30)对于低速流体在同一管道的流动问题,如果考虑流体的局部阻力损失,为何还必须同时考虑流体的黏性损失?
有关工程流体力学基础的文章

伯努利方程是能量守恒定律在流动液体中的表现形式。因而液体AB 段在Δt 时间流动时动能变化为:根据动能定理,外力所做功的总和等于液体能量的增量,即故有:将上式两边分别除以Δmg,整理得:或式和式称为理想液体的能量方程,一般称为理想液体的伯努利方程。式称为实际液体的伯努利方程。......
2023-06-18

研究低速流体力学问题的计算公式主要为流率守恒公式与伯努利方程式这两个,研究的重点放在流动流体流速和压力的变化上。对于低速流动,使用伯努利方程式研究流体流动时压力与速度的变化,其计算结果与实际测量结果之间的误差其实不大,以致于可以将误差忽略不计。......
2023-06-29

通过统计分析表2—10,我们仍然将所有作出了教育服务贸易开放承诺的“一带一路”国家分为三类进行统计分析。具体分析如下所述。在发达国家方面,教育服务贸易市场准入承诺的部门覆盖率平均为73.33%。其中有只有1个国家对所有5个教育服务贸易分部门中都作出了承诺,占20%;有3个国家对其中的4个分部门的市场准入作出了承诺,占60%;有1个国家对其中的2个分部门市场准入作出了承诺,占20%。......
2023-11-18

平行混合是混合特征中最简单的方法,平行混合中所有的截面都相互平行,所有的截面都在同一窗口中绘制,截面绘制完毕后指定截面的距离即可。平行混合又分为规则截面和投影截面两种。图4-91 截面3图4-92 切换截面图4-93 对话框图4-94 输入截面2的深度图4-95 输入截面3的深度图4-96 直线连接的平行混合曲面从图4-96中可以看出,所有的棱边均为直线,且为开放口,即在中的栏中的→选项。1)单击选项卡组中的→选项,系统将自动弹出对话框。......
2023-06-19

由于Engelund-Hansen公式是针对粒径相对均匀的沙质河床而建立的,所以Kd修正的适用性应采用沙质河流中具有较大σg值的非均匀沙资料进行检验。表2-5用于检验Kd修正的水槽试验和天然河流资料情况由此得到式中的b值为1.2。由此可以认为,对σg小于1.5的数据,修正因子Kd对输沙率的修正可以忽略,而对σg大于2的数据,计算精度则显著提高。......
2023-06-22

对症止头痛,其实很简单头痛是一种常见的病症,常发生在多种急慢性疾病中,有时更是某些相关疾病加重或恶化的先兆。中医学认为头痛是由于外感或内伤,致使脉络绌急或失养;清窍不利所引起的头部疼痛。其症状表现为患者自觉头部包括前额、额颞、顶枕部位疼痛。近年来头痛在我国的发病率呈上升趋势,尤其是偏头痛。其症状为头痛较剧烈、经常发作、治疗比较困难。......
2023-12-05

弹弓的使用方法简单,拉开牛皮筋,产生一定的拉力后,采取“三点一线”瞄准法,以嘴角、“Y”中心点至远方的目标,发射即可。忽然,妈妈发现从一个草地里射出一个弹珠,知道是虎子的弹弓射出来的,立刻跑过去,救出了虎子。现在市场上有很多弹弓,根据自己的力气、身高,买一个即可。如果不购买弹弓,可以找材料自己做。生存技能大考验小涛自己制作了一个弹弓,但是无法射出子弹。......
2023-11-17
相关推荐