泵的排量为:图2.5外啮合齿轮泵工作原理式中D——齿轮分度圆直径,D=mZ;h——有效齿高,h=2m;b——齿轮宽;z——齿轮齿数;m——齿轮模数。因此,齿轮泵的流量公式为:低压齿轮泵可选择2πk=6.66高压齿轮泵可选择2πk=7从式2.10 可看出齿轮泵流量和主要参数的关系如下:①泵的排量与齿轮模数的平方成正比。在转速不变的条件下,齿轮泵的流量不能改变,所以齿轮泵属定量泵。......
2025-09-29
文氏流量计的测速原理及应用
【摘要】：3.3.1 测速原理文氏流量计是一种用来测量封闭管道中单相稳定流体流速的测速装置，常用于测量空气、天然气、煤气、水等流体的体积流率或流速，通常所测的流体流动是液体与低速气体流动。
3.3.1 测速原理
文氏流量计（Venturi flowmeter）是一种用来测量封闭管道中单相稳定流体流速的测速装置，常用于测量空气、天然气、煤气、水等流体的体积流率或流速，通常所测的流体流动是液体与低速气体流动。它在测量低速流体流动时的设计原理和空速计一样，都是利用伯努利原理设计的测速装置，也就是其测速公式在稳态一维、不可压缩与非黏性流体的假设下获得。
3.3.2 测速公式
如图3-13 所示，文氏流量计是指测量管道中流动流体的体积流率或流速，它由收缩段、扩散段及两端之间的喉道组成并与U形压差计接通。文氏流量计水平放置，流体管道截面1的面积为 A1，压力为P1，速度为V1，液体或低速气体的密度为 ρ1，截面2的面积为 A2、压力为 P2，速度为V2，液体或低速气体的密度为 ρ2以及 U 形管内的液柱高度差为h。
图3-13 文氏流量计测速原理示意图
温馨小提醒
在如图3-13所示文氏流量计装置中，由于管道内流动的为低速气体，可以假设 ρ1=ρ2，但是管道内流体与U形管的流体并非同一种流体，切不可以混为一谈。(https://www.chuimin.cn)
【例3-4】
如果喷嘴的管件如图3-13 所示，流体比重S为 0.85 的油经喷嘴射出，截面 1 的直径d1=10 cm ，截面2的直径 d2=4 cm ，U形压差计测量出的压力差为7×105 Pa，求截面1与截面2的流速V1与V2。
【解答】
【例3-5】
试证明文氏流量计测量的是低速气体流速，流量计U形管内使用的液体是水，则其测量点2的流速计算公式为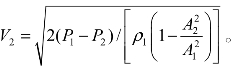
【解答】
（1）因为管内的空气流速缓慢，可以将空气的密度变化忽略不计，也就是 ρ1=ρ2。
相关文章
- 详细阅读
-
的原理及应用光伏系统中变换器的原理及应用详细阅读
光伏发电系统通常分为独立发电系统和并网发电系统。独立光伏发电系统是孤立的发电系统，主要应用于偏远地区。因而光伏并网发电系统可作为分布式能源发电系统的一种有益补充。图5-14给出了典型光伏并网发电系统的结构示意图。图示光伏发电系统中的变换器包括光伏直流电压升压变换器、蓄电池充电控制器、、DC/AC逆变器等。在光伏发电系统用变换器中，光伏并网逆变器是整个光伏并网发电的核心。......
2025-09-29
-
应用奈氏判据的例子详细阅读
例5-9 系统开环传递函数为应用奈氏稳定判据分析闭环系统稳定性。完整的开环幅相频率特性如图5-40所示。例5-12 设系统的开环传递函数为图5-42开环幅相频率特性试用对数频率稳定判据判断闭环系统的稳定性。图5-43系统伯德图由图5-43可见，在L（ω）＞0区段，相频特性曲线φ（ω）负穿越-180°线一次，根据奈氏稳定判据，N+≠N-，即闭环系统不稳定。......
2025-09-29
-
逆向创新的原理及应用详细阅读
逆向创新原理是从反面、从构成要素中对立的另一面分析，将通常思考问题的思路反转过来，有意识地按相反的视角去观察事物，寻找解决问题完全颠倒的新途径、新方法。逆向创新法也称反向探求法。当今世界上大量的新技术、新成果都是人们利用逆向创新原理不断探索创造出来的，是用传统思想方法所无法想象的。我国宋代司马光砸缸救小孩的故事，就是逆向思维方法，他不是将小孩拉出来而是用砸破水缸让水流走的办法，将小孩救出。......
2025-09-29
-
活塞式蓄能器的工作原理及应用详细阅读
图8-16所示为活塞式蓄能器工作原理图。当手动滑阀5在图示位置时，柱塞泵6的柱塞在重力作用下缩回，液压泵1通过单向阀2向蓄能器3供油。当油压升高到一定值时，卸荷阀4动作，液压泵1卸荷，单向阀2阻止蓄能器3的高压油返回液压泵。突然停电或液压泵发生故障、液压泵中断供油时，蓄能器能提供一定的油量作为应急动力源，使执行元件能继续完成必要的动作。......
2025-09-29
-
化学能的计算原理及应用详细阅读
因为比例常数取决于标准化学势基点的选择，所以要赋予一个常数mol-1。由质量守恒原则，给出如下等式：dU=dnB （6-5）因此，对于给定摩尔数的化学反应，它的化学能的量的变化值等于参与反应的两物质的化学能的差。ΔrGAB=μB-μA （6-6）根据Lewis关系，假设两种物质都是理想状态，可以将此值表示为因此，每个化学反应都可以用反应标准摩尔自由焓ΔrGABΘ来表示；至少，在反应物质的量相同时，使评价反应释放或消耗能量的多少成为可能。......
2025-09-29
-
理解SVPWM调制原理及应用详细阅读
SVPWM的调制频率是三角波频率，三角波频率越高，电压谐波减小，这与SPWM调制是一样的，SVPWM是三角波与电压矢量时间系数K的比较，计算量较小，可以使系统响应更快。......
2025-09-29
-
综述：继电器的结构、工作原理及应用选用详细阅读
继电器是根据某种特定形式的输入信号接通或断开小电流控制电路，实现远距离自动控制和保护的自动电器。按用途可分为控制和保护继电器。图1-23 继电器特性1.熟悉继电器的结构和工作原理及其用途。......
2025-09-29
相关推荐