低速流体力学的流率守恒和伯努利方程式

研究低速流体力学问题的计算公式主要为流率守恒公式与伯努利方程式这两个，研究的重点放在流动流体流速和压力的变化上。

3.2.1 流率守恒公式

流率守恒公式根据流体在稳态一维流动状态下的质量守恒定律推导而得。其在热力工程、流力工程以及低速空气动力学的问题中常用来计算管道出入口的质量流率和体积流率或者系统或装置在研究区域内的流体流速变化。

1．质量流率与体积流率的定义与关系

要了解流率守恒公式首先必须知道质量流与体积流率的定义，虽然本书在第1章的内容中已经有说明，但是为了方便学习，仍然根据两者的定义与彼此之间的关系加以简要描述。

（1）两者的定义。

所谓质量流率（Mass flow rate）是指在单位时间内流过管道某一截面的流体质量，用符号表示，单位为 kg/s。所谓体积流率（Volume flow rate）是指在单位时间内流过管道某一截面的流体的体积，用符号Q表示，单位为 m3/s。在质量流率与体积流率的定义公式=ρAV与Q=AV中，分别为流体的质量流率、体积流率、流体密度、流体流经管道的截面积，而V为流体的平均流速。

（2）两者的关系。

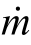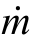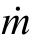对于稳态一维低速流体流动问题，由于流体的密度ρ可视为一个固定常数。又根据质量流率与体积流率Q的计算公式，可以获得流体在稳态一维低速流动时，质量流率与体积流率两者之间的关系为=ρQ =ρAV或者也就是流经管道截面积的质量流率是流体密度ρ与体积流率Q的乘积。

2．流率守恒公式的物理定义与计算公式

流率守恒公式是根据流体在稳态流动状态下的质量守恒定律推导而得。其物理定义为“流体在稳态流场中流进管道的质量流率总和等于流出管道的质量流率总和”。根据这一个定义，可以得到流率公式的计算方程为式中，左边是流进管道的总质量流率，右边是流出管道的总质量流率。如图3-3所示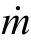，1为流入管道的质量流率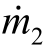，与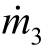为流出管道的质量流率，根据流率守恒公式，得 = +。

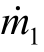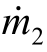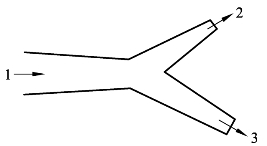
图3-3 分歧管路

对于工程流体力学与低速空气动力学问题，也就是液体与低速气体流动的问题，由于液体与气体的密度变化忽略不计，因此可以将的关系式化简为 Q1=Q2+Q3，其中 Q1为流入管道的体积流率，Q2、 Q3为流出管道的体积流率。可以进一步推导得出，对于同一流管，如果只有单一的进口与出口，则液体与低速气体流过流管任意截面的体积流率都是相同的，也就是 Q=AV= constant ，因此液体与低速气体流速的大小与截面积的大小成反比，如图3-4所示。

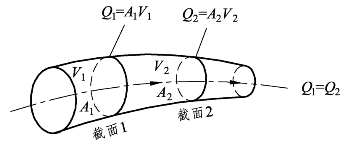
图3-4 在低速流管中面积与流速变化关系

【例3-1】

如图3-5所示，有一个低速风洞的进口截面积为 A1、空气的压力为P1、速度为V1、密度为 ρ1。而风洞测试段内的截面积为 A2，且 A2=0.8A1。假设空气的密度保持不变，而且摩擦损失亦可不计，问截面2的速度是多少？

图3-5 低速风洞流动

【解答】

假设空气的密度保持不变，可以用体流率守恒公式求出V1与 V2之间的关系。

因为 Q1=Q2⇒ A1V1=A2V2，所以可以得出。

【例3-2】

如图3-6 所示，有一输水管，水自截面 1 流向截面 2，测得截面 1 处的水流平均流速V1=2 m/s ，已知输水管道在截面1的管道直径 d1=0.5 m ，在截面2的管道直径d2=1 m，问截面2处的平均流速V2是多少？

图3-6 输水管道流动

【解答】

（1）因为在截面1的管道直径 d1=0.5 m ，在截面2的管道直径d2=1 m，所以截面1的管道面积截面2的管道面积3.141 6 m2。

（2）根据体流率守恒公式 Q1=A1V1=Q2=A2V2，所以。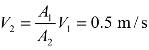

3.2.2 伯努利方程式

日常生活中可以观察到流体流速发生变化时，流体压力也相应发生变化。例如，向两张纸片中间吹气，两纸不是彼此分开，而是相互靠近。两条并行的游船，船体与船体之间也会越行越近。通常研究液体与低速气体流动的问题时，使用伯努利方程式来计算流体压力与速度变化的关系。

1．使用条件

伯努利方程式（Bernoulli equation）是能量守恒定律在流体力学中的具体表达，形式简单，意义明确，是工程实践中应用非常多的一个方程式。其使用的条件是假设流体为稳态流动、无热与功的传递、不可压缩与非黏性的流场，也就是假设流体的密度变化与黏性效应可以忽略不计。对于低速流动，使用伯努利方程式研究流体流动时压力与速度的变化，其计算结果与实际测量结果之间的误差其实不大，以致于可以将误差忽略不计。但是对于高速气流，使用伯努利方程式计算气体流动时压力与速度的变化与实际测量结果之间的误差，却不能忽略，且误差会随着气体的流速增加而逐渐变大。因此对高速气流、黏性流体或者计算精确度有特殊要求的工程问题，必须视实际需要做进一步的修正。

2．公式介绍

伯努利方程式（Bernoulli equation）是伯努利于1738年首先提出的，该方程式表明，对于理想流体在重力场中作稳态流动时，沿着同一流线流动的流体，其静压、动压与位势压的总和会等于某一个固定的常数，也就是流动流体的压力、速度与位置的变化必须满足= constant的关系式。式中，P1与P2分别指流动流体在该测试点的静压，ρ为流体密度，V1与V2分别指流动流体在该测试点的流速，g为重力加速度，而z1与z2分别是流动流体在直角坐标上测试点的垂直方向的位置高度，并以向上的方向为正。必须注意的是，在不同流线上静压、动压与位势压的总和构成的常数值通常是不相同的，所以一个伯努利方程式只能应用于一条流线上的不同点。对于流体在单一流管内低速流动的问题，由于引入了平均流速的概念，所以伯努利方程式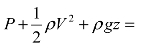constant仍然适用，不过在式中，V指的是流动流体在该测试点的平均流速。另外，虽然伯努利方程是假设低速流动流体的密度不会随着流体的流速而改变，但实际上密度会随着区域的位置与高度有所不同，所以使用伯努利方程研究低速气体流体时，必须先行确定研究区域所在位置的气体密度。

3．物理意义

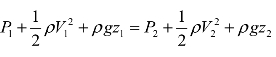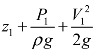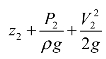由伯努利方程的关系式= constant ，推导出= constant ，式中，z1与z2分别是流体质点在直角坐标上的垂直方向的位置，称为位置水头（Position head），其物理意义是流体质点在该测试点的位能（Potential energy）具有的位势高度（Potential height）。与分别是流体质点在测试点压力作用下能上升的高度，称为压力水头（Piezometric head），其物理意义是流体质点的压力能（Pressure energy）具有的压力势高度（Pressure potential height）。与分别是指流体质点在真空中以初速V1与V2垂直向上喷射能达到的高度，称为速度水头（Velocity head），其物理意义是流体质点的速度能（Velocity energy）具有的速度势高度（Velocity potential height）。而与分别是流体质点于测试点位置水头、压力水头与速度水头的总和，称为总水头（Total head），其物理意义是流体质点的位能具有的位势高度与压力能具有的压力势高度以及速度能具有的速度势高度这三种高度之总和。因此伯努利方程式的物理意义又可以表示为“理想流体在重力场中作稳态流动时，沿着同一流线流动的流体，其位置水头、压力水头与速度水头的总和，也就是总水头必定会保持在某一个固定的常数，因此总水头线会是一条水平线”，如图3-7所示。

图3-7 伯努利方程式物理意义

4．静压、动压与总压的物理定义

在许多工程应用中，流体的流动是在同一水平面或者与其他流动参数相比，坐标z变化可以忽略不计，例如皮托管与空速管的测速计算，通常伯努利方程中把流体在测试点之间的位置高度差，也就是位势压差造成的影响忽略不计。因此伯努利方程式能够简化为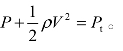式中，P与和 Pt分别表示流体质点在测试点的静压、动压与总压。

（1）静压的物理定义。

在伯努利方程式中，P称为静压（Static pressure），它是指流动流体在测试点上承受到静止流体的压力。

（2）动压的物理定义。

在伯努利方程中，称为动压（Dynamic pressure），它是指流体流动产生的压力，也就是流速造成的压力。

（3）总压的物理定义。

在伯努利方程式中，Pt称为总压（Total pressure），它是指静压与动压的总和。

对于一个稳态一维的理想流体，如果在流体流动过程中能够将位势压差造成的影响忽略不计，则流动流体的静压与动压的总和，也就是总压保持不变，因此流体在流速快的地方静压小，而在流速慢的地方静压大，这就是伯努利定理要表达的基本内容。必须注意的是，从伯努利方程式中能够看出对于单一进出口的管流，流体的流速增加会造成流体的静压降低。对于液体而言，当压力降低到饱和蒸气压力以下，液体气化会造成空蚀现象（Cavitation），此时伯努利方程式将不再适用。综合连续方程和伯努利方程，可得到以下结论：在低速气流中，空气稳定地流过一根粗细不同的流管时，流管细的地方流速快，静压小；流管粗的地方流速慢，静压大。这就是低速气流的主要特性，是分析飞机低速飞行空气动力产生和变化的基本依据。

5．伯努利方程式在工程上的实际应用

伯努利方程式通常广泛地应用于热力工程、流体机械以及水力工程等工程测量低速流体流动的速度，可以说是工程实践中应用得非常多的一个方程。一般而言，使用最多的是皮托管测量装置、空速计测速以及文丘里管测速等测速装置，文丘里管测速装置还必须配合体积流率守恒公式以求出管内流体流动的速度或流率，这里仅对皮托管测速与空速计测速加以描述及说明。

1）皮托管测速装置

皮托管测量装置（Pitot tube measurement device）主要用来测量管内流体的流速，由皮托在 1773年首次使用于测量塞纳河的流速因而得名，其工作原理如图3-8 所示。装置在流场中的某点放置一根两端开口的直管，其测量到的是点1的压力，也就是静压，因此该管也称为静压管（Static pressure pipe），在另一点处放置一根两端开口的直角弯管，其一端迎着来流的方向，当流体流进直角弯管并上升一定高度后，管内流体就静止了，因此点2处的流速为零，形成驻点，驻点处的压力称为总压，所以此直角弯管称为总压管（Total pressure pipe）。

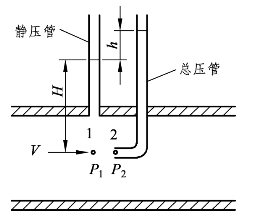
图3-8 皮托管测量装置的工作原理

根据伯努利方程，总压 Pt与静压P之间的压力差为动压等于总压管与静压管之间两液柱液面高度差形成的液压差ρgh，因而流动流体在管内流速计算公式为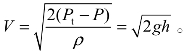从公式中可以发现，只要能够知道总压管与静压管之间两液柱液面高度差h，即可推知管内流动流体的流速V。由于皮托管的安装会造成流体微弱的扰动而产生微小的压差阻力，所以精确计算还要对测速公式乘以一个流速修正系数Cv，也就是必须将测速公式修正为式中，流速修正系数Cv由实验测得，一般在 0.97～0.99。工程计算为简化起见，非常近似地取 Cv=1，也就是假设皮托管的安装对管流的流动并不会造成影响。

【例3-3】

如图3-9 所示，假设流经皮托管装置的为理想流体，密度为ρ，求解点 2 的速度值V2，并用总压管与静压管的液面高度差h表示压力差 P2-P1与点1的速度值V1。

图3-9 皮托管装置

【解答】

（1）点2为停滞点，所以V2=0。

（2）在点 1 承受的压力为 P1=Pa+ρgH ；在点2所承受的压力为 P2=Pa+ρg(H+h)。式中，Pa为当时的大气压力。所以P2与P1之间的压力差为 P2- P1=ρg(H+h) - ρg H=ρgh 。

（3）根据伯努利方程，可以得到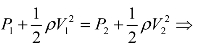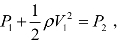所以。

（4）由上述（2）与（3），可以得到因此。

2）空速计的设计原理

空速计（Airspeed indicator）是用来测量飞机飞行速度的装置，它利用皮托管测量装置改良而得，工作原理仍为伯努利原理。工程实践中，静压管包围在总压管的外面，并在总压孔之后适当距离的外壁上沿圆周开设静压孔，使用时将总压孔的通路和静压孔的通路分别连接于空速计的两端，就计算出飞机的飞行速度，其外观示意图如 3-10 所示。设计原理是利用空速管的总压孔来收集空气气流的总压，并利用空速管周围的一圈小孔，也就是静压孔来收集大气的静压，总压与静压之间的差值就是飞机飞行速度产生的动压。

值得必须注意的是空速计的速度计算公式是根据伯努利方程推导得出的，计算结果会因为流体的流动速度和黏性而与实际飞行速度有差异，而且误差值会随着飞行速度的增加而逐渐变大。因此飞机在高速飞行时，计算的飞行速度必须加以进一步的修正。有关修正方式，本书会在后续的内容描述。除此之外，如果空速计为U形压差计，也就是其外观示意图改为如图3-11 所示，则测量流体的流速V计算公式必须改为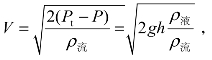式中，Pt与P分别是测量流体的总压与静压，ρ流与ρ液分别是测量流体的密度与U形压差计内液体的密度，而g为重力加速度。

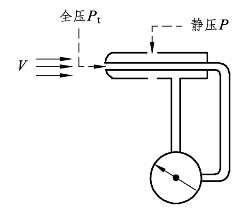
图3-10 空速计的外观示意图

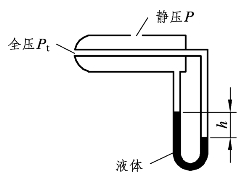
图3-11 U形压差计的外观

6．马格努斯效应

马格努斯效应（Magnus effect）是伯努利方程的一种变形应用，它是空气动力学的现象，由马格努斯发现，所以以他的名字来命名。它可以说明在球类运动中棒球的曲球、足球的香蕉球以及乒乓球的抽球等原因。

（1）定义。所谓马格努斯效应是指一个旋转物体的旋转角速度向量与物体飞行速度向量不重合时，在与旋转角速度向量和移动速度向量组成平面相垂直的方向上会产生一个横向力，使物体的运动轨迹发生偏转的现象，这里以棒球的上、下飘球为例，说明马格努斯效应的发生原理。

（2）原理说明。根据伯努利定律，流体速度增加将导致压力的强度减小，流体速度减小将导致压力的强度增加，这样就导致旋转物体在横向的压力差，因而形成横向力，物体的飞行轨迹发生偏转，如图3-12 所示。根据相对原理，物体在运动时，相对气流流动的方向与物体运动的方向相反，所以如果棒球向右运动，相对气流流动的方向是向左的。对于一个向右投出的棒球，如果棒球逆时针旋转，由于流经球体上方气流的流速被迭加，气流的流速增加，而流经球体下方气流的流速被抵消，气流的流速减少。球体下方气流的流速小于上方气流的流速，根据伯努利定律，球体下方的压力大于上方，因此棒球会向上飘移。反之，如果棒球向右以顺时针的方向旋转投出，则将会是下坠球。

图3-12 上飘球原理