低速流体力学问题中的流体假设与实验验证

2023-06-29 理论教育版权反馈

【摘要】：研究低速流体力学问题经常使用的假设主要有稳态一维流动、不可压缩流体、非黏性流体、理想流体、平均流速与流管等。因此采用非黏性流体假设的结果都必须利用实验来检验其精确度与可用性。

研究低速流体力学问题经常使用的假设主要有稳态一维流动、不可压缩流体、非黏性流体、理想流体、平均流速与流管等。

3.1.1 稳态一维流动

由于流体连续性（Fluid continuity）的假设，通常在研究低速流体力学问题时会将液体与气体的压力P、温度T和密度ρ等流体流动性质与流体流速V表示为位置和时间的函数，所谓稳态流动（Steady flow）的假设是指流体的压力P、密度ρ和温度T等流体流动性质以及流体的流速V随着时间产生的变化量都非常小，以致于可以将流体的流动性质与流速因为时间产生的变化量忽略不计。而一维流动（One-dimensional flow）的假设则是假设流体的流动性质与流速仅随着单一空间坐标而改变，也就是流体的流动性质与流速可以仅用单一空间坐标的函数来表示。综合前面的内容所述，所谓稳态一维的流体流动（Steady one-dimensional flow）就是假设流体的流动性质与流速不会随着时间产生变化并且可以使用单一空间坐标的函数来表示。稳态一维的流体流动是一种最简单的理想化流动模型。由于流体在空间内的实际流动一般都不是真正的一维流动，但是在研究过程中可以将整个流场划分成许多流管，在每一个十分细小的流管中，流体的流动就可以近似看成一维流动。除此之外，由于在同一坐标对应的截面上的各状态参数通常也并非完全均匀，截面上的各状态参数，可以通过采用取平均值的方法，将实际流动当作一维流动来近似处理。在流体流动处于稳定以及对于研究问题精确度要求不高的工程问题研究中，稳态一维流动的假设可以大幅地降低问题研究的难度，此处理模式通常广泛地应用于热力工程、流体机械以及水力工程等研发与设计之中，可说是工程实践中应用非常多的一个假设。

3.1.2 不可压缩流体

所谓不可压缩流体（Incompressible fluid）是假设流体流动时密度变化量非常小，以致于流体流动时的密度变化可以忽略不计，也就是将流体流动时的密度ρ视为常数，即ρ= constant 。实验和研究都已证实，液体流动与气体流速低于 0.3马赫（Ma）流动时，密度变化通常可以忽略不计。不可压缩流体的假设可以将流体流动时产生的压缩性忽略不计，从而使问题研究简单化，大幅地降低研究流体流动问题的难度。

3.1.3 非黏性流体

流体在实际上是具有黏性（Viscidity），在流体流动时会产生一个阻滞流体流动或者对于在流体中运动的物体造成一个阻碍物体运动的作用力，此作用力称为黏滞阻力（Viscous resistance）或简称为阻力（Drag）。在流体力学理论发展的初期，因为流体黏性对流体流动在数学建模以及公式的计算上带来极大困难，因此学者在处理某些低速流体流动问题时将流体的黏度μ假设为 0，这就叫作非黏性流体（Inviscous fluid）假设。虽然非黏性流体假设会大幅地简化研究过程遭遇的难度，但是在实际中，根据假设计算与分析得到的结果往往会影响问题的精确度，甚至结果会发生与实际现象不同的情况。因此采用非黏性流体假设的结果都必须利用实验来检验其精确度与可用性。

3.1.4 理想流体

所谓理想流体（Ideal fluid）假设是将流体流动时的密度变化与黏性通通忽略不计，也就是假设流体在流动时，流体密度ρ的变化与流体的黏度μ均为 0。简单地说，理想流体的假设必须同时满足“不可压缩流体”与“非黏性流体”的假设。它是一种假想的流体，因为任何流体的流动实际上都是具有黏性的运动。虽然使用“理想流体”的假设可以大幅地简化流体流动问题计算或求解的难度，但仅能解决某些低速流体流动的问题，而且通常利用“理想流体”的假设研究得到的结果必须配合某些已知实验成果与实践经验来检验其计算结果的精确度、可用性及正确性。

3.1.5 平均流速与流管的概念

一般而言，研究低速流体流动问题时通常会使用流管与平均流速的概念以简化研究的难度，虽然它们是一个假想的概念，但是在工程流体力学或空气动力学的问题研究中，却是一个非常有用而且不可或缺处理模式。

1．流管的概念

流体的流线不仅可以清楚地表述流体流动的方向，而且在流场内，流线的疏密还反映了流速的大小，因此使用流线能够明确地表示流体的运动情况。在流场中取任意一条不是流线的曲线C，并在曲线C上的每一点做一流线，如果曲线C为一条非封闭曲线，这些流线所构成的曲面称为流面（Stream surface），如图3-1（a）所示。如果曲线C是一条封闭曲线，则这些流线所构成的管状曲面称为流管（Flow tube），如图3-1（b）所示。

pagenumber_ebook=65,pagenumber_book=58

图3-1 流面与流管

流管的侧表面由流线组成，根据流线的定义：在流线上每一点的速度向量都在该点与流线相切，且在稳定流场中，流场流线的流速并不会随着时间改变，所以在稳定流动时，流管的形状不会随着时间的改变而改变，在流管以内或以外的流体质点只能始终在流管以内或以外流动，不能穿越管壁。从这个意义上来说，流管虽然只是一个假想的管子，但是其却可以像真实的固体管壁，把流管内外的流体完全隔开。在研究稳定流场中的流体流动问题时，可以利用流管的概念将流场局限在某特定区域中，这样就大幅地简化研究问题的难度，如图3-2所示。

pagenumber_ebook=65,pagenumber_book=58

图3-2 流管概念

在流管内部的全部流体称为流束，流束可大可小，其大小视流管所取的封闭曲线大小而定，如果流管所取的封闭曲线是管道周围内部壁面时，则其流束就是充满管道内部的全部流体。如果流管所取的封闭曲线是流经飞机壁面到边界层厚度之间的范围时，则其流束就是充满流经飞机外部边界层区域的所有流动气体。流管的选取通常必须视研究问题的需要而定。

2．平均流速的概念

在工程计算中，为了方便，引入了平均流速的概念，它是一种假想的流速。其假设流体在低速流动，也就是流体流速小于0.3马赫（Ma）时，流体流经某一个流管截面上的体积流率（Volume flow rate）都是相等的。平均流速（Mean velocity）定义为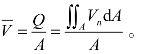 pagenumber_ebook=66,pagenumber_book=59 式中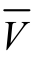，为平均流速，Q为体积流率，A为截面面积，Vn为流体流经流管截面的法向速度。人们所常说：在某一管道中某种流体的流速是多少，其中的流速就是指平均流速，平均流速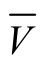上的横杠往往不予标出，而以V表示。当然，除了速度外，严格地说，截面上的各压力与温度的值也不会是完全均匀的，此时可以将流管截面上流体的压力和温度值通过取平均值的方法做近似处理。一般而言，对于大多数的流体流动分析，通常并不需要知道流管截面上流速的精确分布，而只需得到流管截面的平均流速，也就是从体（积）流率守恒公式或平均流速的定义计算中获得流速。根据研究指出，在湍流情况下的流管截面速度分布比较平坦，所以流体的平均流速基本就是流管内中轴线处的流速。在层流情况下，流体的平均流速则为流管内中轴线处流速的一半。

低速流体力学问题中的流体假设与实验验证

相关推荐