图3-12圆锥体表面上点的求作已知投影图;M 点投影图的求作;K点投影图的求作;素线法求作N 点的投影;辅助圆法求作N 点的投影1.求作M 点的H 面和W 面投影M 点的V 面投影在点划线上,且V 面投影可见,则M 点在最前素线上。圆锥底面的V 面和W 面投影积聚成直线,所以K点的V 面和W 面投影图可利用底面的积聚性和投影规律求作,如图3-12 所示。......
2023-06-22
前面已经讨论了静止液体中压力的分布规律,但是在实际工程设计中,例如水箱、水闸、挡水墙以及其他水工设施的设计时,不仅要知道静止流体的压力大小和分布,还要确定流体作用在物体壁面上总力的大小、方向和作用点。
2.6.1 静止液体对容器壁面造成的影响
如图2-18 所示形状不同而底面面积均为 A 的四个容器,如果装入同一种液体且高度也完全相同,自由液面上均作用着大气压力Pa,根据静压理论,沉浸在静止液体的物体,其承受的压力与物体的沉浸深度成正比,且浸液深相同,物体承受的总压也就相同。所以作用于四个容器底面上的总压力必然相等,而与容器的形状无关,又因为自由液面承受的压力与容器外环境的大气压力相等,所以彼此之间可以相互抵消,可以推得容器底部壁面所受的作用力为 FP=ρghA。式中,ρ是液体的密度,g是重力加速度,h是液体的沉浸深度,而A为容器底部壁面的面积。必须特别注意的是如果自由液面上的压力与容器外环境的大气压力并不相等,则必须考虑容器内外之间压力差对容器壁造成的影响。
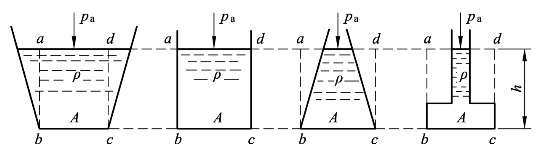
图2-18 底面相同而形状不同的几种容器的壁面承受力
2.6.2 静止液体对平面壁面所产生的作用力
由于静止流体的压力系随高度呈线性变化,因此流体静力学的问题可简化为仅关于平板截面的形心(Centroid)以及转动惯量(Moments of inertia)的问题。如图2-19所示为任意形状之平面板完全沉浸在液体中的情形。以平面板倾斜方向为y轴,与y轴垂直的方向为x轴。

图2-19 平板上所受流体作用力
1.总压力作用力的计算
在平板上任取微元面积dA,其中心点距自由表面的距离为h,距Ox轴的距离为y,由液体的静压理论可以得知,其上的流体压力垂直指向平板。作用在微元面积dA上的压力为dF=PdA=ρg hdA=ρgy sinα d A ,式中F、 P、 ρ、g、 h 与A分别为静止液体压力对壁面所产生的作用力、静止液体的压力、液体的密度、重力加速度、液体的沉浸深度和平面壁面的面积。将dF =ρg y sinα d A 的关系式两边积分得![]() 等于平板面积 A与其形心Ox轴的距离yc的乘积,可得 F =ρg ycsinα A=PcA ,由此静止液体压力对平面壁面产生的作用力等于受压面形心c处的压力与平面壁面面积的乘积。
等于平板面积 A与其形心Ox轴的距离yc的乘积,可得 F =ρg ycsinα A=PcA ,由此静止液体压力对平面壁面产生的作用力等于受压面形心c处的压力与平面壁面面积的乘积。
2.作用力的位置
静止液体压力对平面壁面作用点称为压力中心(Center of pressure),假设其坐标位置为(xp、 yp),根据理论力学中合力矩定理,也就是合力对任一轴的力矩等于各分力对同一轴的力矩之和,可以求得对Ox轴的惯性矩(Moment of inertia)Ix的关系计算公式为![]() ,式中F、P、 ρ、 g、 α、y 与Ix分别为静止液体压力对壁面产生的作用力、静止液体的压力、液体的密度、重力加速度、平面板与液面水平面的夹角、平面板与y轴(平面板倾斜方向为y轴)的垂直距离以及Ox轴的惯性矩,其中
,式中F、P、 ρ、 g、 α、y 与Ix分别为静止液体压力对壁面产生的作用力、静止液体的压力、液体的密度、重力加速度、平面板与液面水平面的夹角、平面板与y轴(平面板倾斜方向为y轴)的垂直距离以及Ox轴的惯性矩,其中![]() 整理上式得
整理上式得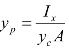 ,根据惯性矩的平行移轴定理
,根据惯性矩的平行移轴定理![]() 可得受压面对通过形心 c 且平行于Ox轴的形心轴的惯性矩Ic,进而推得形心在y轴的位置
可得受压面对通过形心 c 且平行于Ox轴的形心轴的惯性矩Ic,进而推得形心在y轴的位置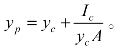 同理可得到压力中心 p 的另一个坐标位置为
同理可得到压力中心 p 的另一个坐标位置为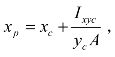 式中,Ixyc为受压面对通过形心c且平行于Ox、Oy轴的形心轴惯性积。
式中,Ixyc为受压面对通过形心c且平行于Ox、Oy轴的形心轴惯性积。
在实际工程中,受压面多以Oy轴对称,此时压力中心必定在对称轴上,因此通常可以不去计算xp。许多虽非完全对称的平面,也常常可以分成几个规则的面积来计算。
3.综合归纳
(1)研究重点。在工程领域中,静止液体对平面壁面产生影响的研究重点多放在总压力作用力的计算与作用点位置的判定上。
(2)作用力的计算。从前文可知,静止液体对平面壁面产生总压力作用力的大小仅与沉浸液体密度、受压面形心c处的沉浸深度与平面壁面面积有关,而与其他因素无关。
(3)作用点位置的计算。静止液体压力对平面壁面作用点称为压力中心,假设其坐标位置为(xp,yp),其作用点位置的计算公式为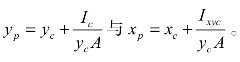 在实际工程中,受压面多以Oy轴对称,此时压力中心必定在对称轴上,通常可以不去计算xp。几种常见平面形状的面积 A、 yc与Ic列出如图2-20所示。
在实际工程中,受压面多以Oy轴对称,此时压力中心必定在对称轴上,通常可以不去计算xp。几种常见平面形状的面积 A、 yc与Ic列出如图2-20所示。

图2-20 几种常见平面形状的面积 A、yc与Ic的参考数值
【例2-10】
水平底床之渠道宽 1.2 m,设有闸门控制流量如图2-21 所示,若关上闸门时上游水深0.8 m,求(1)闸门所受之力;(2)压力中心的位置为何?

图2-21 例2-10闸门承受水压力
【解答】
(1)根据作用力的计算公式 F=PcA=ρg ycsin αA=ρghcA ,其中 面积A=b×h= 1.2 × 0.8=0.96 m2。所以作用力 F=ρghcA= 9.81×1000× 0.4× 0.96=3 767 (N)。
面积A=b×h= 1.2 × 0.8=0.96 m2。所以作用力 F=ρghcA= 9.81×1000× 0.4× 0.96=3 767 (N)。
(2)根据计算公式,压力中心的位置为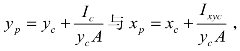 又因为Oy轴对称,此时压力中心必定在对称轴上,因此xp可以不去计算。而从图2-20 几种常见平面形状的yc与Ic中可得
又因为Oy轴对称,此时压力中心必定在对称轴上,因此xp可以不去计算。而从图2-20 几种常见平面形状的yc与Ic中可得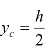 与
与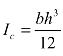 。因为面积A=bh,所以
。因为面积A=bh,所以
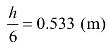 。
。
【例2-11】
如图2-22 所示,一矩形闸门两面受到水的压力,左边水深 H1=4.5 m ,右边水深H2=2.5 m,闸门与水平面成α=45°的倾斜角,假设闸门宽度b=1 m。试求作用在闸门上的力。
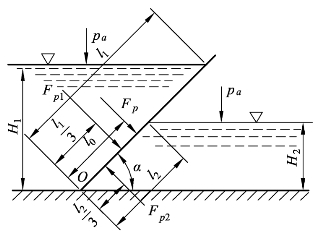
图2-22 例2-11闸门承受水压力
【解答】

2.6.3 静止液体对曲面壁面产生的作用力
在工程技术中,例如各类圆柱形容器、储油罐、球形压力罐、水塔、弧形闸门等的设计,都会遇到静止液体作用在曲面上总压力的计算问题。由于作用在曲面上各点的流体静压产生的作用力都垂直于容器壁,这就形成了复杂的空间力系问题。工程中用得最多的是二维曲面且三维曲面与二维曲面的计算方法类似,所以本书以静止液体作用于二维曲面壁面产生的影响为例来说明。静止液体对二维曲面壁面产生影响的问题研究与前面讨论的对平面壁面产生影响的问题研究几乎一样,研究的重点只不过因为作用壁面是曲面,各微元面上的压力dF的方向不同,作用力不能直接积分来获得,必须先求水平分力和铅垂分力,然后再求合力。
1.作用力的计算
如图2-23所示为液体在曲面壁面上作用力情况,假设液面通大气,也就是液面表压力为零,静止液体压力对二维曲面壁面产生的水平分力为 Fx,铅垂分力为 Fz,而水平分力 Fx与铅垂分力 Fz两个分力的合力为静止液体压力对二维曲面壁面产生的作用力,与二维曲面壁面两者的交点处即为作用点。
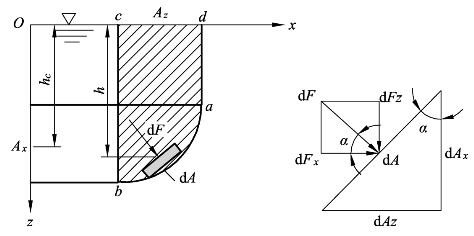
图2-23 液体作用在二维曲面壁面上作用力情况
(1)水平分力的计算。
静止液体压力对二维曲面壁面产生的水平分力 Fx可以用计算公式![]() ρg hcAx计算。式中,ρ、g、 hc、 Ax分别为液体的密度、重力加速度、受压面形心 c 在液面下的沉浸深度与该曲面壁面在铅垂方向的投影面积。可以看出,液体作用在曲面壁面上水平分力的大小等于该曲面铅垂投影面上所受作用力。
ρg hcAx计算。式中,ρ、g、 hc、 Ax分别为液体的密度、重力加速度、受压面形心 c 在液面下的沉浸深度与该曲面壁面在铅垂方向的投影面积。可以看出,液体作用在曲面壁面上水平分力的大小等于该曲面铅垂投影面上所受作用力。
(2)铅垂分力的计算。
静止液体压力对二维曲面壁面产生的铅垂分力 Fz可以用计算公式![]() ρg V 。式中,V为曲面ab上的液柱体积abcd,这样的体积通常称为压力体。可以看出,液体作用在曲面壁面上铅垂分力的大小等于压力体的液体重力。
ρg V 。式中,V为曲面ab上的液柱体积abcd,这样的体积通常称为压力体。可以看出,液体作用在曲面壁面上铅垂分力的大小等于压力体的液体重力。
(3)合力的计算。
由于液体作用在曲面壁面上的作用力F等于液体作用在曲面壁面上水平分力 Fx和铅垂分力 Fz的合力,所以![]() 。
。
2.作用点位置的获得
液体作用在曲面壁面上的铅直分力 Fz的作用线通过压力体的重心指向受压面,且因为液体作用在曲面壁面上的水平分力 Fx的作用线通过 Ax的压力中心而指向受压面。所以液体作用在曲面壁面上的作用力必通过铅直分力 Fz的作用线与水平分力 Fx的作用线的交点,并与铅垂分力 Fz的作用线成θ夹角,而其作用线与曲面的交点就是液体作用在曲面壁面上的作用点,如图2-24所示。
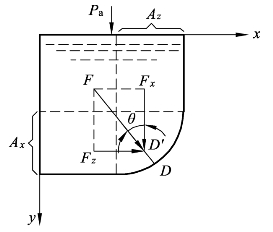
图2-24 静止液体对二维曲面壁面作用力与作用点
【例2-12】
如图2-25 所示,有一圆柱扇形闸门,已知H1=5 m,α=60°,闸门宽度B=10 m,试求在闸门上的作用力。
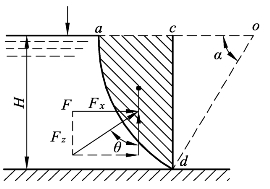
图2-25 例2-12闸门受力
【解答】
(1)液体对曲面壁面产生的水平分力 Fx的计算公式为 Fx=ρghcAx,式中 Ax为该曲面壁面在铅垂方向的投影面积。由题干可知 Ax=BH。可得水平分力![]()
![]() 因此
因此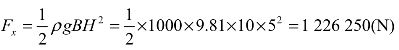 。
。
(2)液体对曲面壁面产生的铅垂分力 Fz计算公式为 Fz=ρgV,式中,V为曲面上的压力体,由题干可知 V=B×Aabc,而面积Aabc为扇形面积aob与三角形面积cob的差值,故铅垂分力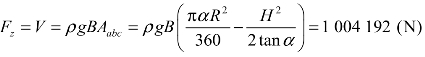 。
。
(3)根据合力的计算公式得![]() 。
。
有关工程流体力学基础的文章

图3-12圆锥体表面上点的求作已知投影图;M 点投影图的求作;K点投影图的求作;素线法求作N 点的投影;辅助圆法求作N 点的投影1.求作M 点的H 面和W 面投影M 点的V 面投影在点划线上,且V 面投影可见,则M 点在最前素线上。圆锥底面的V 面和W 面投影积聚成直线,所以K点的V 面和W 面投影图可利用底面的积聚性和投影规律求作,如图3-12 所示。......
2023-06-22

泡沫质量是指在一定的温度和压力下,泡沫流体中的气体体积与泡沫体积之比,也称为泡沫干度或泡沫特征值。泡沫是一种不稳定流体,当泡沫静止不动时,小泡沫会有向大气泡中扩散的倾向,小气泡变成大气泡后,大气泡就会因为浮力的作用逐渐上升。因此泡沫是一种复杂的流体,它的性能会受到很多可变因素的影响。......
2023-11-18

10.4.1 动能修正系数10.4.2 管流能量损失实际流体在管道内的流动过程中因为流体的黏滞效应或流经障碍造成机械能的损失称为管流能量损失,其形成的机理和计算方法各有不同,为了便于分析,常将能量损失分为沿程阻力损失和局部阻力损失两类。......
2023-06-29

图12-53 设置入口边界图12-54 设置入口速度Step3:选择分析树中的Boundary命令,在Boundary Condition面板的Zone中选择coolinlet选项,在图12-55所示的Type栏中选择velocity-inlet选项。在弹出的图12-56所示的velocity-inlet对话框中作如下设置:在velocity Magnitude(m/s)栏中输入入口流速为10m/s;在Specification Method栏中选择Intensit yand Viscosity Radio选项;在Turbulent Intensity(%)栏中输入5,在Turbulent Viscosity Radio栏中输入10;在Thermal选项卡中输入温度为300K,并单击OK按钮。图12-55 设置出口边界图12-56 设置入口速度Step5:设置outlet为Pressure Outlet属性,如图12-57所示,在属性框中保持所有参数默认即可。......
2023-10-20

2.不适用情况将流体作为连续介质来处理流体静止或流动时的性质变化,对于大部分工程技术问题都是准确的。在研究黏性流体力学时,流体的黏性通常用动力黏度,又简称为黏度来表示,并将黏性流体视为牛顿流体。......
2023-06-29

图2-1 流体静压定义与其作用方向的示意图2.2.2 静压的计算实验表明在静止流场中,液体和气体承受的相对压力,仅与液体或气体的密度和高度有关,而与其他因素无关,这个结论即称为静压理论。根据静压理论计算公式与前面推得 PB=PC的结果,可进一步推得关系式 PB=PA+ρ1ghAB=PC=P0+ρ2ghCD。......
2023-06-29

流体力学主要是研究流体在静止或流动时性质变化以及流体流动时对流场内的物体造成的影响,因此在式学习流体力学前必须对流体的性质与速度有一定的认识,才能对后续的学习内容有清楚而完整的认识。显然,流体的比容ν为流体的密度ρ的倒数,并可表示为。......
2023-06-29

第 10 章已经探讨了黏性流体的内部流动,也就是管流问题。本章将讨论黏性流体流经物体外部表面的问题,也就是黏性流体的外部流动。对于有些问题的研究,使用非黏性流体假设可以简化研究过程,又不会影响问题的基本结论,但是在许多实际应用中,流体与接触物体表面不可能不产生黏性作用,使用非黏性流体的假设不仅影响工程计算的精度,甚至获得的结果还会和物体实际运动产生的物理现象相互矛盾,例如达朗贝尔悖论就是一个例子。......
2023-06-29
相关推荐