边界层内的流体发生分离时,本章前面内容导出的边界层计算公式不再适用。此外,实验又发现,物体运动时受到的阻力不仅和物体表面的粗糙度有关,也与分离点的位置有关,飞机在亚声速飞行时,气流产生流体分离的现象会引起飞行升力急速下降,因而产生失速,造成飞机安全事故,甚至导致机毁人亡的事情发生。因此流体分离的现象一直是飞机、船舶与车辆在外形设计时必须考虑的非常重要的课题。......
2023-06-29
流体处于静止状态时的压力,称为流体的静压,用符号 P 表示,单位为Pa(或N/m2)。静压理论主要是探讨静止状态时压力变化的基本规则,其在航空工程与流体机械工程中应用甚广。
2.2.1 流体静压作用的方向
流体具有不能抵抗剪应力的特性,所以在受到剪应力就会产生连续的变形,就会产生流动。流体在静止时受到的剪应力τ必定为 0,而其静压作用的方向必定与作用面垂直,并指向作用面的内法线方向,如图2-1所示。
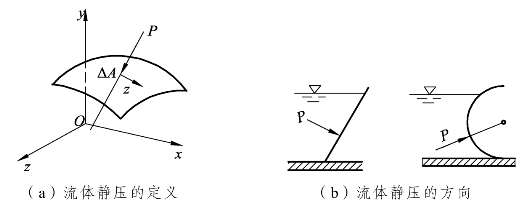
图2-1 流体静压定义与其作用方向的示意图
2.2.2 静压的计算
实验表明在静止流场中,液体和气体承受的相对压力,仅与液体或气体的密度和高度有关,而与其他因素无关,这个结论即称为静压理论(Static pressure theory)。根据静压理论与连续介质的假设,可以将液体和气体在静止状态时压力变化的规律用计算式![]() 来表示,式中,P 是指液体或气体在静止时承受的压力,z 是指在直角坐标系的垂直方向的空间变量,并以向上的方向为正,ρ是指液体或气体的密度,而 g 是重力加速度,其值约为9.81 m/s2,静止压力随着高度变化如图2-2所示。
来表示,式中,P 是指液体或气体在静止时承受的压力,z 是指在直角坐标系的垂直方向的空间变量,并以向上的方向为正,ρ是指液体或气体的密度,而 g 是重力加速度,其值约为9.81 m/s2,静止压力随着高度变化如图2-2所示。

图2-2 静止压力随着高度变化
2.2.3 静压理论表示的物理意义
根据静压理论的计算公式![]() 将静压理论计算公式的两边积分可以得到P2- P1=-ρ g(z2- z1),因为h是液体或气体在静止时流场内质点1与质点2的差,因此可得P2- P1=ρgh ,从而推得 P2=P1+ρgh 。式中,P2、 P1、ρ、g 与h分别表示流体在静止状态下流场内部流体质点2与质点1受到的压力、流体的密度、重力加速度和两个质点之间的高度差。
将静压理论计算公式的两边积分可以得到P2- P1=-ρ g(z2- z1),因为h是液体或气体在静止时流场内质点1与质点2的差,因此可得P2- P1=ρgh ,从而推得 P2=P1+ρgh 。式中,P2、 P1、ρ、g 与h分别表示流体在静止状态下流场内部流体质点2与质点1受到的压力、流体的密度、重力加速度和两个质点之间的高度差。
1.影响静压的因素
从推导 P2=P1+ρgh 的结果可知,在静止流场中,液体和气体内各个质点承受的压力差,仅与液体或气体的密度和高度有关,与其他因素无关。
2.静压变化的规律
在静止液体或静止气体内的物体,其承受的压力与物体所处位置有关。物体沉浸得越深,承受的压力越大。而在静止流场中,同一平面的每个质点,彼此间的压力差为0。
由此可知,人在爬山的时候,越往高处,承受的压力越小,而且飞机在高空飞行时承受的压力比在地面时的压力低。这也是为什么爬山者会产生高山症,而飞机的空调必须增压的原因。
【例2-1】
如图2-3所示,一个玻璃杯,直径为7.2 cm,倒入8 cm高的水,试计算水的表面与杯底间的压力差。
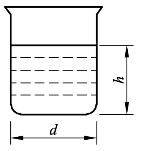
图2-3 水杯
【解答】
因为水的密度 ρ= 1 000 kg/m3;水深为 8 cm=0.08 m,所以水的表面与杯底间的压力差为ΔP =ρgh=(1 000 kg/m3)× (9.81 m/s2)× (0.08 m)=785 N/m2。
【例2-2】
试论述静态流体在太空中各个质点的压力差为0的原因?
【解答】
根据静压理论![]() 可以知道,在静止流场中,液体和气体内各个质点承受的压力差,仅与液体或气体的密度、重力加速度和高度差有关,而与其他因素无关。由于在太空中的重力加速度g=0,因此
可以知道,在静止流场中,液体和气体内各个质点承受的压力差,仅与液体或气体的密度、重力加速度和高度差有关,而与其他因素无关。由于在太空中的重力加速度g=0,因此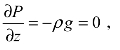 静态流体在太空中内各个质点的压力差为0。
静态流体在太空中内各个质点的压力差为0。
【例2-3】
如图2-4所示,容器中有两层彼此之间互不掺混的液体,密度分别为 1ρ和 2ρ,试计算图中A,B两点处的压力。
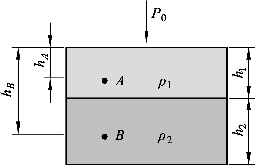
图2-4 液体内部的压力
【解答】
根据静压理论与静压计算公式,可以得到 A 点压力为PA=P0+ρ1ghA,而B点压力为PB=P0+ρ1g h1+ρ2g(hB-h1)。
【例2-4】
如图2-5所示,已知 ρ1=999.2 kg/m 2 ,ρ2=899.7 kg/m 2,P0=101 325 Pa,g=9.81 m/s2,试求容器顶部空气的压力 PA。
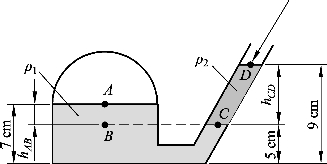
图2-5 容器内流体压力
【解答】
(1)根据静压理论可知,同一种液体或气体与同一平面的每个质点,其彼此之间的压力差为 0。在题干中 B 点与 C 点处于同一种液体的同一平面,所以两点的压力相等,也就是PB=PC。
(2)根据静压理论计算公式与前面推得 PB=PC的结果,可进一步推得关系式 PB=PA+ρ1ghAB=PC=P0+ρ2ghCD。
(3)所以 PA=P0+ρ2ghCD- ρ1ghAB=101 325+899.7 × 9.81×4 - 999.2 × 9.81×2=117 025 (Pa)。
有关工程流体力学基础的文章

边界层内的流体发生分离时,本章前面内容导出的边界层计算公式不再适用。此外,实验又发现,物体运动时受到的阻力不仅和物体表面的粗糙度有关,也与分离点的位置有关,飞机在亚声速飞行时,气流产生流体分离的现象会引起飞行升力急速下降,因而产生失速,造成飞机安全事故,甚至导致机毁人亡的事情发生。因此流体分离的现象一直是飞机、船舶与车辆在外形设计时必须考虑的非常重要的课题。......
2023-06-29

因为比例常数取决于标准化学势基点的选择,所以要赋予一个常数mol-1。由质量守恒原则,给出如下等式:dU=dnB (6-5)因此,对于给定摩尔数的化学反应,它的化学能的量的变化值等于参与反应的两物质的化学能的差。ΔrGAB=μB-μA (6-6)根据Lewis关系,假设两种物质都是理想状态,可以将此值表示为因此,每个化学反应都可以用反应标准摩尔自由焓ΔrGABΘ来表示;至少,在反应物质的量相同时,使评价反应释放或消耗能量的多少成为可能。......
2023-06-22

具有分散控制、信息集中管理特点的分布式计算机控制系统称为集散控制系统。集散型控制系统的结构通常分三级:第一级为直接过程控制级,第二级为集中操作监视级,第三级为综合信息管理级。典型DCS系统结构图如图5-1-18所示。......
2023-06-26

图13-10 音波的传播压力波经过压力为p和密度为ρ的气体时,会发生无限小的变化,即dp、dρ、dV。因此,音波经过后的流体状态变化为速度dV、压力p+dp、密度ρ+dρ,如图13-10b所示,引用以固定在波面的坐标,流体以波面为中心右侧以速度a接近,左侧以速度a-dV远离。dh-adV=0 式中,流体速度变化量dV很小,可以忽略其平方项。通常,音波的能量很小,不能改变流体的温度或压力。......
2023-06-28

流体发电已经被报道用于能量转换以及流体流速和溶液浓度的检测。通常,有两种类型的流体通道能够用于流体发电。图4.57MFG中微流控芯片的制造和表征[7]采用软光刻技术制造微流控芯片;具有设计结构的Si模具照片;图案化PDMS复制品的图像;PDMS复制品上的微柱阵列的SEM图像,插图为高放大倍数下,视角为30°时PDMS结构的图像;透明微流控芯片的图像Peng等制备出一种纤维状流体纳米发电机。图4.59纳米管中的流动发电过程......
2023-06-30

FEKO默认采用SEP方法计算介质体,该方法采用三角形网格剖分。2)当对于涂层的相对介电常数与金属线所在的媒质相同时,应用等效理论计算体极化电流。......
2023-10-31

定义长度单位单击“Home”菜单中的“Model unit”按钮,在“Model unit”对话框中,选中“Millimetres”单选按钮。磁芯几何尺寸:lx=64;ly=3;lz=8。漆包线与磁芯的间隔:gap=0.1。每个导线向x轴偏移的距离:gapx=0.255。在CADFEKO左侧的树形浏览器中,选中“Media”结点,单击鼠标右键,选择“Metallic medium”选项,创建有限电导率金属。设置磁芯的求解方法为VEP。图5-55 设置磁芯材料的求解方法在“Construct”菜单中,单击“Line”按钮,弹出“Create line”对话框,如图5-56所示,进行如下设置。......
2023-10-31

对云服务提供商而言,由于云计算服务不需要将软件安装在用户的计算机中,降低了商业软件被破解的风险。就目前的情况来看,云计算正在颠覆世界各地企业的IT消费方式,采用云计算模式可带来许多好处和优势。云计算服务供应商承担对云计算平台和服务进行全天候的监控和维护。用户可以在权限许可下共享云计算平台中的数据。这一特性使得云计算服务能够允许云端的节点出现错误甚至是崩溃。......
2023-11-18
相关推荐