探讨迹线、烟线和流线的关系

2023-06-29 理论教育版权反馈

【摘要】：为了更加明确地描述流体运动，这里引入迹线、烟线和流线的概念，如图1-17 所示。一般来说，对于非稳态的流场，流线、烟线与迹线三者并不重合。

为了更加明确地描述流体运动，这里引入迹线、烟线和流线的概念，如图1-17 所示。

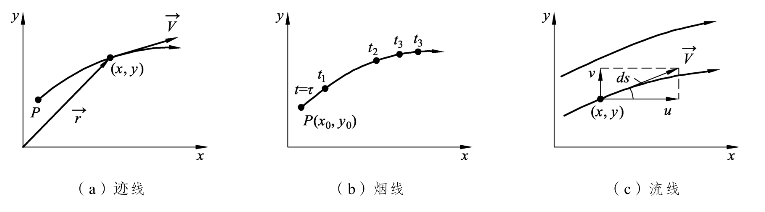
pagenumber_ebook=30,pagenumber_book=23

图1-17 迹线、烟线与流线的概念示意图

1.9.1 迹线

所谓迹线（Path line）是某一特定流体质点的运动轨迹，如图1-17（a）所示。因为流场中有无穷多个流体质点而且每一个流体质点在运动的时候都有一条运动轨迹，所以流场中的迹线会有无穷多条。考虑流体质点是以局部速度随着流体运动，所以迹线必须满足方程式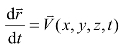 pagenumber_ebook=30,pagenumber_book=23 。

1.9.2 烟线

所谓烟线（Streakline）是指由先后连续地经过同一个固定点的流体质点所形成的曲线，如图1-17（b）所示。例如喷气飞机在天空留下的飞行云，就是在同一时刻，流经喷嘴的空气流动分子形成的，归属于烟线。因为烟线是在某一瞬间将所有曾经通过空间中某一特定位置的流体质点于目前所处的位置连接成的轨迹，所以可以利用通过（x0，y0）点的迹线方程式并配合当t=τ时，x=x0，y=y0的初始条件求出烟线方程式。

1.9.3 流线

所谓流线（Stream line）是指在给定时刻与流体质点运动速度向（矢）量相切的各点所形成的曲线，如图1-17（c）所示。由于在流线上每一点的速度向（矢）量都在该点与流线相切，因此使用流线可以清楚地表达流体流动速度的方向，如图1-18 所示。对于三维流场流线而言，流线必须满足方程式 pagenumber_ebook=30,pagenumber_book=23 至于二维流场的流线必须满足的关系式。

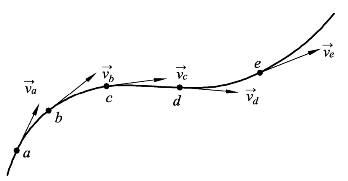
pagenumber_ebook=31,pagenumber_book=24

图1-18 流线与流速关系示意图

流体流场的流线不会彼此相交，如果有两条流线彼此相交，那么位于交点上的流体质点势必有两个不同方向的速度。所以在一般情况下，流场的流线彼此相交的情况不可能存在，除了三种情况：一种是速度为 0 的点，称为前驻点（Front stagnation point），如图1-19（a）所示A点；另一种是后驻点（Rear stagnation point），它是指物体表面上下速度相交的各点，如图1-19（a）所示 B 点；还有一种是速度为无限大的奇异点（Singular point），如图1-19（b）所示O点。

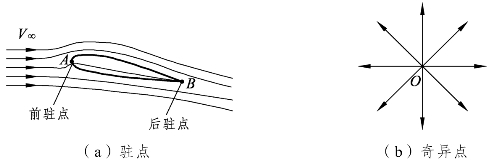
pagenumber_ebook=31,pagenumber_book=24

图1-19 驻点与奇异点

流体的流线不仅可以清楚地表述流体流动的方向，而且在流体流场内，流线的疏密还反映了流速的大小。流线疏的地方流速小，流线密的地方流速大。因此使用流线可以明确地表示流体的运动情况。需要特别注意，流线是与时间相互对应的，不同的时刻可以有不同流线。

1.9.4 三者重合的时机

对于一个非稳态的流场，流体速度会随着时间的变化而改变，不同时刻的流线是不同的，因此流线和个别流体质点的运动轨迹（迹线）会有所差异。而在非稳态的流场中，个别流体质点的运动轨迹（迹线）也不会和流场的烟线相同。一般来说，对于非稳态的流场，流线、烟线与迹线三者并不重合。但是如果流场是稳态的话，由于速度不会随着时间变化，流线、烟线与迹线三者合而为一。

1.9.5 学习建议

本章节描述有关流线、迹线与烟线的概念中，学习重点主要在于三者的定义。附后有关稳态流场与非稳态流场的判定以及流线、迹线与烟线方程式的计算等四个例题的练习虽然有助于对流体力学与空气动力学理论的认知，但根据实际教学经验，如果学生对流体运动参数的向（矢）量描述方式没有一定程度的认识，不仅不能获得预期效果，反而会因为耗费过多的时间去研究例题，从而丧失学习的兴趣。所以在此建议应先行掌握流线、迹线与烟线三者的定义与概念，然后学习第6章“流体流动参数的描述”的内容后，再来练习附后的四个例题，如此将能够事半功倍。

【例1-17】

如果一个已知的二维流场在x轴与y轴方向上的速度分量分别为 u=x(1+2t)、v=y，其中x，y并非是t的函数，请问此流场是否为稳态，为什么？

【解答】

因为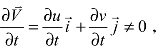 pagenumber_ebook=32,pagenumber_book=25 所以此流场不是稳态，为非稳态流场。

【例1-18】

如果一个已知的二维流场在x轴与y轴方向上的速度分量分别为u=x、v=y，其中 x，y并非是t的函数，请问此流场是否为稳态，为什么？

【解答】

虽然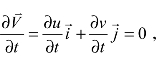 pagenumber_ebook=32,pagenumber_book=25 但是如果一个流场是稳态，则必须满足流体的流动性质（压力、密度、温度）和流速对时间t的偏微分都等于0，所以该流场不一定是稳态。

【例1-19】

如图1-20 所示，如果一个已知的二维流场在 x 轴与 y 轴方向上的速度分量分别为u=x(1+2t)、v=y，请求出

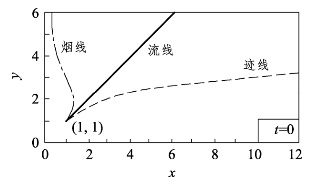
pagenumber_ebook=32,pagenumber_book=25

图1-20 例1-19流场

（1）在t=0时通过位置（1,1）的流线（Stream line）方程式。

（2）在t=0自位置（1,1）释出流体质点的迹线（Path line）方程式。

（3）在t=0时通过位置（1,1）的烟线（Streakline）方程式。

【解答】

（1）流线方程式的求解过程。

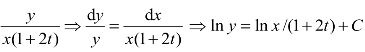① 因为二维流场的流线必须满足的关系式，所以可以推得 pagenumber_ebook=33,pagenumber_book=26 。

② 因为当t=0时 x=1，y=1，代入步骤①导出的关系式中，因此可以推得C=0，且y=x1 /(1+2t)。

③ 将t=0代入步骤②导出的关系式中消去时间 t，因此可以获得当t=0时的流线方程式为x=y。

（2）迹线方程式的求解过程。

① 因为二维流场的迹线必须满足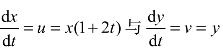 pagenumber_ebook=33,pagenumber_book=26 两个条件，将两方程式积分推得 x=C1exp[t (1+t)]与 y=C2exp(t)。

② 将t=0时通过位置（1, 1）的条件代入 x=C1exp[t (1+t)]与 y=C2exp(t)中可以得到C1=1且C2=1。

③ 由步骤②导出的关系式消去时间t，由此可以得到在t=0自位置（1, 1）释出流体质点的迹线方程式为 x=y1+ln(y)。

（3）烟线方程式的求解过程。

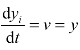① 因为用来求解烟线的方程式是与 pagenumber_ebook=33,pagenumber_book=26 两个方程式，将两个方程式积分，得到 xi=C1exp[t (1+t)]与 yi=C2exp(t)两个关系式。

② 将初始条件（Initial condition）代入步骤①导出的关系式中，当t=τ时，xi=yi=1，因此可以得到 C1=exp- [τ(1 +τ)]与C2= exp(-τ)。

③ 将时间t=0代入步骤①与②导出的关系式中消去时间t，由此可以得到t=0时通过位置（1, 1）点的烟线方程式是 xi=yi1-ln(y)。

（4）综合讨论。

从上面的推导可以证实：如果流体流场是非稳态，流线、烟线与迹线三者不会彼此重合。

【例1-20】

如图1-21 所示，二维空间的稳态流速度场为 V= axi-ayj ，a为常数，试求通过（1, 1）点的流线、迹线与烟线方程式。

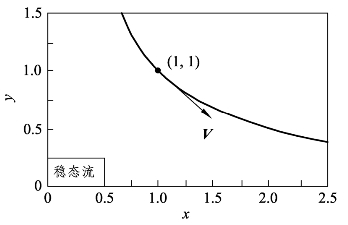
pagenumber_ebook=33,pagenumber_book=26

图1-21 例1-20流场

【解答】

（1）流线方程式的求解过程。

① 从题目可知，该穏态流场在x轴与y轴方向上的速度分量分别为u =ax，v =-ay 。

② 因为二维流场流线必须满足的关系式，可以推得C1或 xy=C2。

③ 因为流体质点通过点（1, 1），代入步骤②导出的关系式中可以推得C2=1，因此可以获得通过（1, 1）点的流线方程式为xy=1。

（2）迹线方程式的求解过程。

① 从题目可知，该穏态流场在x轴与y轴方向上的速度分量分别为u =ax，v =-ay 。

② 因为二维流场的迹线必须满足 u=dx/dt =ax 与 v=dy/dt =-ay 两个条件，将这两个方程式消去dt及常数a可以推得。

③ 将步骤②导出关系式的两边加以积分，可以得到 lny =- lnx+C3或者是xy=C4。

④ 因为流体质点通过点（1, 1），代入步骤③导出的关系式中，可得C4=1且迹线方程式为xy=1。

（3）烟线方程式的求解过程。

① 从题目可知，该穏态流场在x轴与y轴方向上的速度分量分别为u =ax，v =-ay 。

② 因为用来求解烟线的方程式是dxi/dt=u=ax与dyi/dt=v =-ay ，将这两个方程式消去dt及常数a可以推得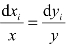 pagenumber_ebook=34,pagenumber_book=27 。

③ 将步骤②导出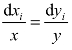 pagenumber_ebook=34,pagenumber_book=27 关系式的两边加以积分，可以得到 ln yi=- ln xi+C5或者xiyi=C6。

④ 因为流体质点都通过点（1, 1），可得C6=1，由此可以得到烟线方程式是 xiyi=1。

（4）综合讨论。

从前面的推导上可以证实：如果流体流场是稳态，流线、烟线与迹线三者会彼此重合。

探讨迹线、烟线和流线的关系

相关推荐