根据上述几何条件，解决平行问题作图的关键是直线的投影必须平行于平面内某条直线在同一投影面上的投影。在图形软件系统中，只要用好投影联系功能和画平行线功能，就能快速解决平行问题的作图问题。例3-29已知△ABC和点D的投影，过点D作一正平线DF平行于△ABC。作图先在△ABC中过点B取一条正平线BE。例3-31已知在△ABC和△FFG中，AB∥EF，试判断这两个三角形是否平行。......
2023-06-28
流体流动问题的分类方法及应用场景
【摘要】：1.8.1 稳态流场与非稳态流场由于流体连续性假设的缘故，通常在研究流体力学问题时都会把流体的压力、温度与密度等流体性质以及流体的流速表示位置和时间的函数。
对于工程问题的研究都是从简到繁、从易到难，流体力学问题的研究也是如此。所以在研究流体力学问题的过程中，通常会从实际出发，在允许的精确度范围内，尽量抓住主要的影响因素并忽略次要的影响因素，以求将问题简化以节省研究问题的时间与成本，这就需要将流体流动的问题加以分类。因为不同的流动类型有着不同的研究方法，其问题的分类如图1-12所示。
图1-12 流体流动问题分类的示意图
在研究流体力学问题时，大抵可以将流体流动问题分成稳态流场与非稳态流场（定常流场与非定常流场）、一维与多维流场、内部流场与外部流场、层流流场与湍流流场、不可压缩流场与可压缩流场以及黏性流场与非黏性流场等类型。
1.8.1 稳态流场与非稳态流场
由于流体连续性假设的缘故，通常在研究流体力学问题时都会把流体的压力、温度与密度等流体性质以及流体的流速表示位置和时间的函数。例如对于一个直角坐标系而言，流体流场的压力、密度、温度与速度可以表示成 P =P(x, y, z, t)；ρ =ρ(x, y, z, t)；T =T(x, y, z, t)；V =V(x, y, z, t)的函数形式。式中，P、ρ、T与V分别是流体流场的压力、密度、温度与速度；x，y，z 是流体质点在直角坐标的空间变量，而 t 则是时间变量。所谓稳态流场（Steady flow field）的假设是指流体流动性质与流速随着时间产生的变化量非常小，以致于可以将其因为时间而产生的变化量忽略不计，这种流体流场又称为定常流场。当流体的流动为稳态流动或定常流动时，可以将流体流场的压力、密度、温度与速度分别表示为 P=P(x, y, z)；ρ=ρ(x, y, z)； T =T(x, y, z)； V =V(x, y, z)。值得特别注意的必须是流体流场中所有的性质及速度的值都不会随着时间变化而改变，那么这种流体流场才能叫作稳态流场或定常流场。只要在流体流场中，有任何一个流体的性质以及流体速度的值随着时间变化而改变，那么这种流体流场就不是稳态流场，而是非稳态流场（Unsteady flow field）或称为非定常流场。在工程技术的问题研究中，对于稳定的流体流动问题通常会将流体的流动形态假设为稳态流场，以降低研究流体流动问题时的难度。
1.8.2 维数化简的观念
流体的流动性质与气体的流速会因为空间坐标与时间的不同而有所变化。如果流体在流动时，其在某方向的性质与流速变化非常小，可以将该方向的变化量忽略不计，这就是维数化简的观念。如果流体在流动的过程中，流体的流动性质与流速必须要使用三个空间坐标的函数来表示，则这样的流动就称为三维流动（Three-dimensional flow）；如果流体的流动性质与流速可以使用两个空间坐标的函数来表示，这样的流动就称为二维流动（Two-dimensional flow）；如果流体的流动性质和流速仅随着单一空间坐标而改变，也就是流体的流动性质和流速可以仅使用一个空间坐标的函数来表示，则这样的流动就称为一维流动（One-dimensional flow）；如果流体的流动性质和流速并不会随着位置与时间的变化而改变，这种流动称为均匀流动（Uniform flow）。在研究流体力学问题的过程中，流体的流动性质与速度会因为流体连续性的假设而表示为位置和时间的函数，所以流体流场是否为稳态流场与维数化简的观念，通常是合并考虑的，流体的流场区分成三维稳态流场、二维稳态流场、一维稳态流场、三维非稳态流场、二维非稳态流场、一维非稳态流场以及均匀流场等形态。流体的流场是稳态流场还是非稳态流场以及维数的选择往往与研究问题的精确度以及研究的物理现象有关，例如研究气体在发动机喷管内的流动时，如果不需要精确地设计发动机尾喷管的情况，往往可以近似地认为在发动机尾喷管内气体的流动参数只沿着喷管轴线方向，也就是如图1-13（a）所示 x 轴方向变化，而将其他方向的变化忽略，这样，原本实际问题的三维流动就简化成了一维流动。如果发动机处于稳定的工作状态，气流在这样简化的流动模块中就是稳态一维流场，而在发动机启动或停车时，由于发动机的工作状态并不稳定，此时喷管内就是一维非稳态流场。又比如均匀气体流过机翼的情况，如果机翼的翼展比翼弦大得多（可看作是无限翼展），且机翼的翼型剖面形状不变，机翼两端的影响可以忽略，也就是将流动参数沿着翼展方向（z方向上）的变化忽略不计，只有在x轴与y轴的方向才有变化，此时气体的流场是二维流场，如图1-13（b）所示。如果机翼的翼展为有限翼展则必须考虑两翼翼端气流的影响，此时流场的流动参数随着x轴、y轴与z轴的位置而变化，因此气体的流场是三维流场，如图1-13（c）所示。
图1-13 维数化简观念的示意图
【例1-12】
对于一个直角坐标系而言，如果流体的压力P、密度ρ、温度T、速度V均可以分别表示为 P=P(x, y)、 ρ=ρ(x, y)、 T=T(x, y)以及 V=V(x, y)的函数形式，请问此种流场的形态为哪种？
【解答】
因为流体流场中所有的性质或速度的值都不会随着时间变化而改变，且流体性质与速度仅表示为两个空间坐标的函数形式，所以此种流场的形态为二维稳态流场。
【例1-13】
如果流体的压力P、密度ρ、温度T、速度V均可以满足
的条件，请问此种流场的形态为哪种？
【解答】
因为流体流场中所有的性质或速度的值都不会随着时间变化而改变，所以此种流场的形式为稳态流场。
1.8.3 内部流场与外部流场
在研究流体力学问题时，可以依据流体流场的位置，分成内部流场与外部流场两种类型。如图1-14 所示，将飞机模型放在风洞中测试，观察的重点如果是空气流动在风洞内部的性质变化，则这种流场就叫作内部流场（Internal flow field）。
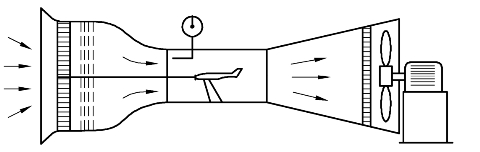
图1-14 飞机模型在风洞测试示意图
又比如飞机在空气中飞行，观察的重点是飞机表面外部气流的性质变化时，则将这种流体流场称为外部流场（External flow field），如图1-15所示。
图1-15 飞机飞行空气流动示意图
通常将流体在管内流动与发动机内部的空气性质变化归属于内部流场问题研究范畴，而将飞机飞行时空气的性质变化、飞行力学与飞行控制等问题归属于外部流场研究。
1.8.4 层流与湍流
如前所述，可以依据流体的雷诺数（Re）将流体流动形态分成层流流场与湍流流场。流体层流流动时，流体作平滑、直线与分层运动，流体质点与质点之间不会混杂和干扰，也就是说流体质点会做规则性运动。而流体湍流流动时，流体流动具有无序性、耗能性与扩散性，所以流体质点的运动呈现不规则扰动，流场中会出现许多小旋涡，两种流场的流动形态如图1-16所示。
图1-16 层流与湍流的流动特性
1.8.5 可压缩流与不可压缩流
根据流体流动的速度，将流体流动的形态分成可压缩流与不可压缩流两种。对于液体或低速流动的气体，密度变化通常可以忽略不计，也就是将流体流速造成的压缩性影响予以忽略，这就是“不可压缩流（Incompressible flow）”的假设，此时即为不可压缩流场。例如飞机在低速飞行，也就是速度低于0.3马赫（Ma）时，飞机表面的空气流速非常小，以致于可以将空气的压缩性对飞行造成的影响忽略不计，从而使问题的研究简单化。实验与研究的结果发现，对于高速流动的气体，也就是流速高于 Ma＝0.3的气体而言，气体的密度变化必须考虑，这种流体的流动称为可压缩流（Compressible flow），此时流体的流场即为可压缩流场。由于气体的压缩性是依据气体的流速加以判定的，所以又将不可压缩流体问题归属于低速流体力学（Low velocity fluid mechanics）研究范畴，而将可压缩流体问题归于高速流体力学（High-speed fluid mechanics）的研究范畴。
【例1-14】
何谓不可压缩流的假设？
【解答】
如果流体是液体或低速流动的气体，也就是流速低于Ma＝0.3的气体，通常将流体的密度变化忽略不计，即流体密度 ρ= constant ，这就是不可压缩流的假设。
【例1-15】
可压缩流与不可压缩流的判定准则为何？
【解答】
可压缩流与不可压缩流的判定准则：如果气体的流速Ma＜0.3，则可判定该气体的流动形态为不可压缩流。反之，可判定该气体的流动形态为可压缩流。
1.8.6 黏性流与非黏性流
流体的黏性是流体的固有特性，任何流体流动或物体在流体流场运动时都不可能没有黏滞效应的产生，所以实际上流体是黏性流体（Viscous fluid）。但是在流体力学问题研究时，流体的黏性对理论分析和数值计算两种方法的数学建模或者计算时间与成本上都会带来极大困难。对于有些低速问题，特别是低速气流的问题，流体的黏性对分析或计算的结果影响甚微以致可以将流体的黏性忽略不计，也就是假设流体的黏度μ=0，这就是非黏性流（Inviscid flow）的假设。虽然对于有些问题的研究，使用非黏性流的假设会大大地简化流体问题研究的复杂度，但是实践中发现，根据非黏性流的假设计算或分析得到的结果往往会影响问题的精确度，甚至会产生得到的结果与实际现象完全不同的情况，引发了许多讨论与修正。所以非黏性流的假设通常只能够使用在工程精确度要求不高，又不会影响问题基本结论的理论计算和研究分析的情况，将在后续的内容中加以详细说明，这里不多加描述。
【例1-16】
何谓非黏性流的假设？
【解答】
在研究低速流体流动的问题时，常将流体流场的黏性造成的影响忽略不计，也就是假设流体的黏度μ=0，这就是非黏性流的假设。
有关工程流体力学基础的文章
- 详细阅读
-
简单一维流体流动的基础特征及应用详细阅读
然而使用理论解析法必须设定某些假设以简化问题来降低研究过程的难度，而简单一维流体流动的数学模型就是流体力学理论发展初期最常用的数学建模方式。虽然使用简单一维流动的假设可以大幅地降低低速流动问题研究的难度，让早期的理论研究得以进一步的发展，但不可否认的是过度的简化问题往往会影响研究结果的可用性与精确度。......
2023-06-29
-
隔离开关的分类及应用场景解析详细阅读
装设隔离开关的最大目的是确实可靠地隔离电源。在相关标准中规定，隔离开关在分断状态下应有明显可见的断口。必要时应在隔离开关上附设接地刀开关，供检修时接地用。图6-22为单柱式隔离开关，隔离开关的静触头被独立地安装在架空母线上。图6-23所示为三柱式隔离开关，与双柱式隔离开关相比，相间距高要求小。三柱式与双柱式隔离开关的基本部件相同，动作原理相似，只是刀开关转动方向不同。......
2023-06-30
-
测量系统的分类与应用场景详细阅读
具有放大器的数据采集卡可配置成差分测量系统。然而，实际应用的板卡却限制了差分测量系统抵抗共模电压的能力，数据采集卡的共模电压的范围限制了相对于测量系统地的输入电压的波动范围。图3-6描绘了一个16通道的RSE测量系统。测量接地信号最好采用DEF或NRSE测量系统。在差分测量系统中，应该保证相对于测量地信号的共模电压在测量系统设备允许的范围之内。......
2023-07-02
-
整经工艺分类及应用场景解析详细阅读
织造生产中的整经工序，根据不同的纱线种类和工艺要求，主要分为分批整经、分条整经等方式，有时根据织物的特殊要求，也有采用分段整经和球经整经方式。(一)分批(轴经)整经1.分批整经 分批整经就是将全幅织物所需要的经纱总根数先分成n 批，每批经纱根数尽可能相等，分别卷绕成n 只经轴，然后将这n 只经轴通过浆纱机 进行并合，按规定长度卷绕到织轴上，为织造工序作准备。......
2023-06-16
-
理解变压器的分类及应用场景详细阅读
变压器的分类方式有很多种，根据其电源相数的不同，可以分为单相变压器和三相变压器。单相变压器可将高压供电变成单相低压，供给各种设备使用。图4-45 单相变压器的功能示意图单相变压器多用于农村输配电系统中，以及一些照明或小型电动机的供电中，其应用实例如图4-46所示。三相变压器主要用于三相供电系统中的升压或降压。......
2023-06-22
-
混凝土输送机械的分类及应用场景详细阅读
混凝土输送机械用来把拌制好的新鲜混凝土及时、保质地输送到浇灌现场。对于集中搅拌的或商品混凝土，由于输送距离较长且输送量较大，为了保证被输送的混凝土不产生初凝和离析等情况，常应用混凝土搅拌输送车、混凝土泵或混凝土泵车等专用输送机械，而对于采用分散搅拌或自设混凝土搅拌点的工地，一般可采用手推车、机动翻斗车、皮带运输机或起重机等机械输送。混凝土的搅拌运输车是一种用于长距离输送混凝土的高效能机械。......
2023-06-29
-
信号发生器的分类及应用场景详细阅读
专用信号发生器是为某种特殊或专用目的而设计制造的，如调频立体声信号发生器、电视信号发生器、编码脉冲信号发生器等。通用信号发生器应用广泛、使用灵活，是一般测试场合不可缺少的重要信号源。正弦波信号发生器应用较为广泛，脉冲波信号发生器主要用来测试数字电路的工作特性，扫频信号发生器用来测试放大电路的幅频特性。......
2023-06-22
相关推荐