流体的性质和速度描述

流体力学主要是研究流体在静止或流动时性质变化以及流体流动时对流场内的物体造成的影响，因此在式学习流体力学前必须对流体的性质与速度有一定的认识，才能对后续的学习内容有清楚而完整的认识。一般而言在研究流体力学问题时，主要是探讨气体的压力、温度、密度、速度与黏性。

1.6.1 压 力

所谓压力（Pressure）是指物体在单位面积上承受正向力的大小，用字母P表示。

1．定 义

如图1-3 所示，物体承受的压力是单位面积上受到的正向力（垂直力），也就是。式中，P 是压力，FN是垂直（正向）力，A是面积。

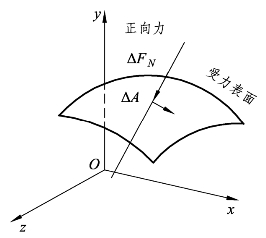
图1-3 压力的定义

压力的单位可以分为标准单位和非标准单位，标准单位是 N/m2 或 Pa，又称为帕斯卡（Pascal），非标准单位则是psi（pound/inch2）或 lb/ft2（pound/foot2）。一般而言，在地表的平均大气压力相当于 76 cm 水银柱的压力，其值约为1.013 25×105 Pa或1.013 25×105 N/m2，也就是俗称的1个标准大气压力。

2．压力的种类

常用的压力可分为绝对压力与相对压力两种，所谓绝对压力（Absolute pressure）是以压力的绝对零值（绝对真空）为基准测量出的压力，用Pabs表示；而相对压力（Relative pressure）是以当地的大气压力为基准测量出的压力，又称为表压（Gage pressure），用Pgage或 Pg表示。绝对压力、大气压力与相对压力之间的关系如图1-4所示。

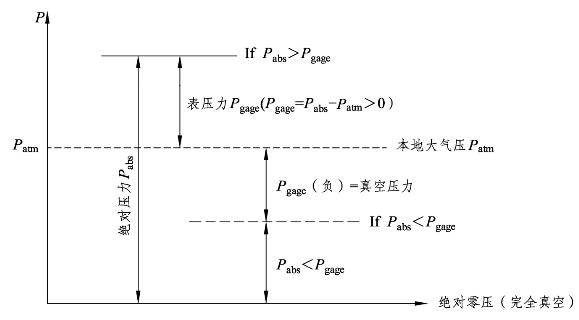
图1-4 绝对压力与相对压力（表压）之间关系

绝对压力与相对压力（表压）之间的转换关系为

虽然在航空界对于压力的表示有两种表示方式，但是在流体力学或空气动力学公式中使用的压力值，都是绝对压力。所以学生在利用理论解析法与数值计算法研究流体力学或空气动力学的相关问题时，必须先将相对压力（表压）换算成绝对压力。

【例1-1】

如果大气压力Patm为98 kPa，而压力表读数为2.25 kPa，试求绝对压力Pabs。

【解答】

因为 Pabs=Patm+Pg，所以绝对压力 Pabs=98+2.25=100.25 (kPa)。

1.6.2 温 度

所谓温度（Temperature）是用来表示物体冷热程度的性质参数，用T表示。

1．定义与类型

在流体力学或空气动力学的问题研究中经常使用的温度包括摄氏温度（°C）、华氏温度（°F）、开氏温度（K）以及朗氏温度（°R）这四种。其中前两种为相对温度（Relative temperature），后两种为绝对温度（Absolute temperature）。在流体力学或空气动力学的公式计算中，采用的温度值，必须是绝对温度。所以摄氏温度或华氏温度在代入流体力学或空气动力学的计算公式中，首先必须先转换成开氏温度或朗氏温度，然后再将开氏温度与朗氏温度分别代入标准单位或非标准单位的计算公式中。

2．转换公式

摄氏温度（°C）、华氏温度（°F）、开氏温度（K）以及朗氏温度（°R）四种类型的温度可以彼此之间进行转换。

（1）摄氏温度（°C）与华氏温度（°F）的换算。

（2）摄氏温度（°C）与开氏温度（K）的换算。

（3）华氏温度（°F）与朗氏温度（°R）的换算。

【例1-2】

若大气温度为25 °C，试转换为华氏温度（°F）、开氏温度（K）以及朗氏温度（°R）。

【解答】

（1）按照公式（1-1），所以+ 32=77 (°F)

（2）按照公式（1-2），所以25+273.15 =298.15 (K)

（3）按照公式（1-3），所以77+459.67=606.67 (°R)

1.6.3 密 度

所谓流体的密度是指每单位体积内包含流体的质量，用ρ表示。其公式定义为

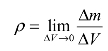
式中，ρ是流体的密度，m是流体的质量，而V是流体占据的体积。对于空间各点密度相同的流体而言，流体密度的计算公式可简化为。水的密度可视为1 000 kg/m3，在地表上的平均大气密度约为 1.225 kg/m3。通常在研究流体力学问题时，可将流体的密度视为常数，但是大气密度的值会随着高度的上升而变小，这是因为随着高度的上升，空气会越来越稀薄的缘故。除此之外，根据实验与研究发现，气体的密度会随着气体所处环境的压力、温度与速度的不同而有所改变。

1.6.4 比容、比重力与比重

在研究流体力学问题时，有很多时候是用其他形式来表示流体的密度，学生必须掌握其与流体密度的转换关系，才能进一步研究流体力学。

1．比 容

所谓比容（Specific volume）是指单位质量中流体占据的体积，用符号ν表示。其公式定义为

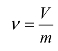
式中，ν是流体的比容，V 是流体占据的体积，而m是流体的质量。显然，流体的比容ν为流体的密度ρ的倒数，并可表示为。

2．比重力

比重力（Specific weight）是指单位体积中流体所受的重力，用符号γ表示。其公式定义为

γ =ρg

式中，γ是流体的比重量，ρ是流体的密度，而g为重力加速度，通常水在一个大气压、4 °C的情况下，比重力为 9 810 N/m3。

3．比 重

比重（Specific gravity）是指流体的密度与水在4 °C时密度的比值，用符号 S表示。其公式定义为

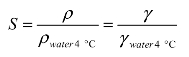
式中，S 是流体的比重，ρ与 ρwater4°C分别是流体的密度以及在一个大气压与 4 °C 的情况下水的密度，γ与 γwater4°C分别是流体的比重力以及在一个大气压与 4 °C 的情况下水的比重力。根据实验与研究的结果，如果液体的比重S小于1.0，也就是S＜1.0，则液体会漂浮在水上，这也是油为什么会漂浮在水上的原理。

4．彼此的关系与转换

（1）流体质量与流体密度之间的关系。根据流体密度ρ的计算公式可以得出流体质量与流体密度之间的转换公式为

m=ρ×V

式中，m是流体的质量，ρ是流体的密度，V是流体占据的体积，也就是流体的质量等于流体密度与流体体积的乘积。

（2）流体比容与流体密度之间的关系。根据流体比容ν与流体密度ρ的定义公式与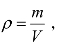可以推出流体比容ν与流体密度ρ转换公式为

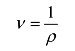
也就是流体比容ν为流体密度ρ的倒数。

（3）流体比重力与流体密度之间的关系。根据流体比重力γ的定义公式γ=ρg，可以推得

也就是流体的密度ρ等于流体比重力γ除以重力加速度g。

（4）流体比重与流体密度之间的关系。根据流体比重 S的定义，可以推得

也就是流体的密度ρ等于流体比重S与水的密度 ρwater4°C乘积。

【例1-3】

如果液体的体积为3 m3，质量为2 850 kg，试求（1）密度ρ；（2）比重力γ；（3）比重S，并判定该液体置于水中是否会浮在水面。

【解答】

（1）根据流体密度ρ的定义，所以。

根据流体比重力γ的定义，所以 γ=ρg=950 kg/m 3 × 9.81 m/s2= 9 319.5 N/m3。

根据流体比重S的定义，所以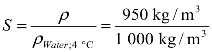= 0.95。

（2）因为液体的比重＜1.0，所以该液体如果置于水中时将会浮在水面上。

1.6.5 速 度

速度（Velocity）是用来衡量物体运动或流体流动快慢程度的参数，在航空航天领域多用马赫数来表示物体运动或气体流动的速度，例如在研究飞机飞行问题时就经常以马赫数的形式来表示飞机的飞行速度。马赫数（Mach number）是物体的运动速度或气体流动的速度对声（音）速的比值，用符号 Ma 表示。其公式定义为

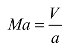
式中，Ma是马赫数，V 是物体的运动速度或是气体流动的速度，a为声速。实验证明液体的密度受温度或压力的影响并不显著，因此通常会把液体的密度视为常数。而对于低速流动的气体而言，也就是气体的流动速度低于 0.3 马赫（Ma）时，通常可以将气体的密度变化忽略不计，但是对于高速流动的气体，也就是气体的流动速度高于0.3马赫（Ma）时，则必须考虑气体的密度变化。除此之外，如果气体流场的局部流速高于声速时，也就是气体流场的局部马赫数大于或等于 1.0时，还必须探讨激波对气体性质造成的影响。通常在地表上大气的平均声速值约为 340 m/s，在离地 10 km 高度也就是大型民航客机的平均巡航高度时，大气的平均声速值约为300 m/s，由此可知对流层内大气的声速值会随着离地表高度的增加而逐渐减少。

【例1-4】

如果一架飞机的飞行速度为150 m/s，声速为300 m/s，请问飞机的飞行马赫数是多少？

【解答】

根据马赫数的定义，飞机的飞行马赫数为=0.5。

1.6.6 质量流率与体积流率

在研究流体力学问题时，通常会使用质量流率来计算流经管道截面面积密度与速度的变化情形，并进而求出流体流场的压力变化。对于液体或低速流动的气体，通常会使用体积流率来计算流经管道截面面积速度的变化情形，从而求出流体流场的压力变化。

1．质量流率的概念

质量流率（Mass flow rate）是指流体在单位时间内流经管道截面面积的质量，用符号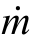表示。其计算公式为=ρAV，式中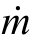，指流体的质量流率，ρ指流体的密度，A指流体流经管道的截面面积，V指流体的平均流速。常有人将质量流率简称为质流率。

2．体积流率的概念

体积流率（Volume flow rate）是指流体在单位时间内流经管道截面面积的体积，用符号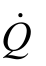表示。其计算公式为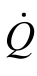=AV，式中，指流体的体积流率，A 指流体流经管道的截面面积以及V指流体的平均流速。常有人将体积流率简称为体流率。

3．两者之间的关系

对于液体与流动速度低于0.3马赫（Ma）的低速气体，由于流体的密度变化可以忽略不计，也就是将流体的密度视为常数，因此流经同一管道截面面积的质量流率与体积流率之间的关系可以用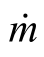= ρA V=ρ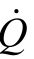的关系式来表示，也就是在流体的密度变化可以忽略不计的情况下，质量流率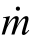等于流体密度ρ与体积流率两者的乘积。

1.6.7 黏 性

由于流体分子与分子之间彼此具有吸引力，流体在流动或物体在流场运动时，流体会产生一个阻滞流体流动或物体在流体中运动的力，这一特有属性，称为流体的黏性，它是流体的固有特性。

1．流体的黏滞系数

在研究流体力学问题时，如果要讨论流体黏性，就必须讨论流体的黏滞系数，而流体的黏滞系数可以分成流体的动力黏滞系数与流体的运动黏滞系数。

（1）动力黏滞系数。根据牛顿黏性定律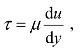式中，τ为流体承受的剪应力，为流体的速度梯度，而μ即为流体的动力黏滞系数（Dynamic viscosity coefficient），又称为流体的动力黏度（Dynamic viscosity），简称为黏度。流体动力黏滞系数的单位为Pa·s，由于黏度单位也常用泊（poise）为单位，用缩写符号 P 表示，且习惯用百分之一的量度，又由于1 poise＝10－1 Pa·s，所以1 cP（centi Poise）＝10－3 Pa·s。

（2）运动黏滞系数。因为流体的黏性对流体流动或物体在流场内运动的影响通常与流体的密度ρ有关，所以在研究流体力学问题时常需引入运动黏滞系数的概念。流体的运动黏滞系数可用公式表示。式中，μ为流体的动力黏滞系数，ρ为流体密度，ν即为流体的运动黏滞系数（Kinematic viscosity coefficient），简称为流体的运动黏度（kinematic viscosity），其单位用1 m2/s或cSt（centi Stoke）表示，而1 cSt＝1 mm2/s。

2．牛顿流体的概念

如果必须讨论流体的黏性问题时，通常会将黏性流体视为牛顿流体。所谓牛顿流体（Newtonian fluid）是指在定温以及定压的情况下，剪应力与流体的速度梯度成正比的流体，也即满足前面说明的牛顿黏性定律（Newton law of viscosity）的流体。除非特别说明或有特殊需求，大家通常都会将流体视为牛顿流体来处理黏性流动问题。

3．无滑流现象

流体具有黏性，因此其流经物体表面时，流体分子与物体接触表面会因为彼此的相互作用，在接触的物体表面达到动量平衡，物体表面接触的流体速度会和接触物体表面的速度相同，这一现象即称为无滑流条件（No-slipping condition）。同理，接触物体表面能达到能量的平衡，因而和物体表面接触的流体温度会和接触物体表面的温度相同，这一现象即称为无温度跳动条件（No temperature jump condition）。在流体力学的问题研究中，无滑流条件与无温度跳动条件主要作为决定黏性流体在接触物体表面时速度与温度的判定原则。

【例1-5】

请问飞机在静止时会有黏性作用的产生吗？

【解答】

所谓流体的黏性是指流体在流动或是物体在流场运动时，流体会产生一个阻滞流体流动或物体在流体中运动的力，静止的飞机因为没有运动，所以黏性作用不会产生。

【例1-6】

假设流体流场的速度分布如图1-5所示，试求与固定平板接触的流体速度u(0)。

图1-5 沿平板流动（1）

【解答】

根据无滑流现象，因为和物体表面接触的流体速度会和接触物体表面的速度相同，所以与固定平板接触的流体速度u(0)=0。

【例1-7】

假设流体流场的速度分布如图1-6 所示且两平行平板相距非常近，试求流体流场的速度分布u(y)。

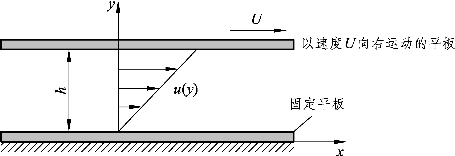
图1-6 沿平板流动（2）

【解答】

（1）根据无滑流现象，因为和物体表面接触的流体速度会和接触物体表面的速度相同，所以流体速度u(0)与u(h)分别为u(0)=0与u(h)=U。

（2）当两平行平板相距非常近时，可以假设黏性流体在两平行平板之间的速度呈线性分布，也就是假设流体流场的速度梯度为一常数。因此可设流体流场的速度分布公式为u(y)=ay+b，式中a与b为常数值。

（3）因为u(0)=0，所以可以推得b值为0。

（4）因为b值为0，且u(h)=U，所以u(h)=ah+b=ah=U ，可以推得。

（5）将与b=0代入流体流场的速度分布公式u(y)=ay+b中可得在两平行平板之间的速度分布为。

【例1-8】

如图1-7所示，气缸的内径D＝152.6 mm，活塞的直径d＝152.4 mm、长L＝304.8 mm，已知润滑油的运动黏度ν=9.144×10 - 5 m2/s ，密度 ρ= 920 kg/m3，活塞的运动速度 U＝6 m/s，试求克服摩擦阻力所需消耗的功率。

图1-7 气缸活塞运动

【解答】

（1）从题目可知，

① 气缸壁与活塞之间的间隙δ为。

② 活塞的表面面积A=πdL。

③ 由于附着在气缸上的润滑油速度为零，附着在活塞上的润滑油速度为 U＝6 m/s，而气缸壁的间隙δ很小，所以可假设油层内的速度呈线性分布，可推得。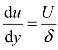

（2）因为作用在活塞上的摩擦阻力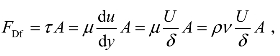因此可求得其值为。

（3）因为克服摩擦阻力所需消耗的功率 P=FDf×U因此可求得其值为 P=FDf×U=736.6 × 6=4 420 (W)=4.42 (kW)。

【例1-9】

如图1-8所示，有一滑动轴承，轴的直径d＝120 mm，轴承长度L＝200 mm，间隙 δ= 1 mm ，其中充满黏度 μ= 0.54 Pa·s 的润滑油，轴承以转速n＝200 r/min运转，试求轴承转动时摩擦力与转动时所需功率P。

图1-8 滑动轴承示意图

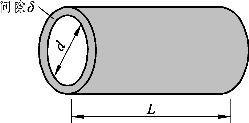
【解答】

（1）由题可知，轴承转动，滑动轴承内油层的速度分布。

（2）轴承转动时摩擦力= 5.118 (N)，而所需的功率 P=FDf×U= 6.43 (W)。

1.6.8 雷诺数

研究黏性流体力学问题时，可以依据雷诺数 Re 将流体流动分成层流流场与湍流流场，因此流体的雷诺数 Re 是判定黏性流体流动形态的一个指标。

1．雷诺数的意义

从物理观点来看，流体的雷诺数（Reynolds number）可以视为流体惯性力（Inertial force）与黏滞力（Viscous force）的比值，用符号Re表示。而从数学上的定义来看，流体的雷诺数Re 可以用计算公式来表示。式中，Re 是雷诺数，ρ为流体的密度，V为流体流动的速度，L 为特征（参考）长度，μ为流体的动力黏度。当流场的雷诺数较小时，黏滞力对流场的影响大于惯性力，流场中流速的扰动会因黏滞力而衰减，流体质点作有规则的运动，流体流场为层流；反之，如果流场的雷诺数较大时，惯性力对流场的影响大于黏滞力，流体质点的运动呈现不规则扰动，流体流场为湍流。由此可知雷诺数的大小决定了黏性流体的流动形态。

2．层流与湍流的特性与区分

实验与研究的结果都已经证实，如果流体流场的雷诺数大于某一数值，流体流场会由层流开始过渡转换成湍流，该雷诺数值称为临界雷诺数（Critical Reynolds number），在层流流场与湍流流场中，流体流动的形态与特性截然不同，描述如下。

（1）层流的特性。

在流体的流动速度很慢的情况下，流体的雷诺数很小，流体质点沿着与管轴平行的方向作平滑、直线与分层运动，因此流体的流动称为层流（Laminar flow）。流体在层流流场中运动时，流体质点与质点彼此之间不会混杂以及干扰，也就是说流体的质点会做有规则的运动。流体的流速在管中心处最大，而在接触壁面处最小。在层流流场中管内流体的平均流速与最大流速之比等于 0.5。层流流体在圆形直管内流速分布如图1-9（a）所示。

（2）湍流的特性。

当流体的流速很慢时，流体的雷诺数小，流体的流动为层流，而随着流体逐渐增加流速，流体的雷诺数逐渐地变大，流体流场会逐渐地由层流转换成湍流（Turbulent flow）。当流体的流动变成湍流时，流体质点的运动呈现不规则扰动，流场中会出现许多小旋涡，因此湍流又被称为乱流、扰流或紊流，其流体形态如图1-9（b）所示。研究指出：湍流的特性大抵包括无序性、耗能性与扩散性三种特性，本书在此依次描述与说明。

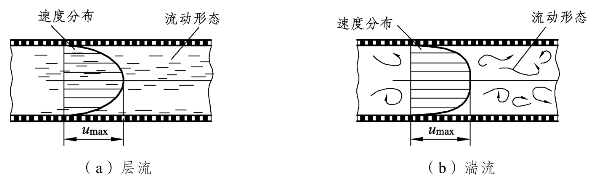
图1-9 层流与湍流的流动特性示意图

① 无序性。当流体流动转换为湍流时，流体的质点做不规则的运动，除了沿主要方向的流动外，还有附加的横向运动，导致流体在流动过程中流体质点间的混杂。

② 耗能性。当流体流动转换为湍流时，除了湍流扰动造成的横向运动会产生附加的剪应力外，还有因为流场中的旋涡引起能量损耗。湍流的摩擦阻力与压差阻力一般会比层流的大，所以在飞行器或船舶设计中，应该尽量使流体边界层的流动保持层流状态。

③ 扩散性。湍流流场因为流场扰动与旋涡的缘故，分子的扩散、传质、传热与动量传递等扩散性能一般会比层流来得大。

由于湍流流体的不规则性，使得其理论研究极为困难，虽然近年来随着科技的进步，高速摄影等测量技术的使用与计算机测量数据处理的简易化，使得研究者对湍流机理、起源及其内部结构有了更深层的认识，但是对湍流流动的研究实际来说，至今还没有一个较为成熟的理论，许多基本问题还不能完满地用湍流理论来解决，目前的研究主要还是利用半经验公式结合实验进行探讨。

【例1-10】

实验证明：湍流的摩擦阻力与压差阻力一般会比层流来得大，请问其原因何在？

【解答】

因为流体流动从层流转换为湍流时，除了湍流扰动造成的横向运动会产生附加的剪应力外，还有流场中的旋涡会引起能量损耗，所以一般而言，湍流的摩擦阻力与压差阻力一般会比层流来得大。在飞行器或船舶设计中，应该尽量使流体边界层的流动保持层流状态。

（3）流动状态判别的准则。

雷诺在 1883年时根据实验提出了层流与湍流这两种流动状态判定准则，其实验装置如图1-10所示。

图1-10 雷诺实验装置

雷诺发现在流体流动速度很慢的情况下，流体的雷诺数很小，有色液体呈一条直线平稳地流过整根玻璃管而与管内的水不混合，这说明管内流体质点是作有规则地平行流动，质点之间互不干扰，这种流动形态称为层流，其流动状态如图1-11（a）所示。在有色液体流动不变的情况下，调整控制阀以增大水流速度，从而增加雷诺数，当流体的雷诺数增大到一定数值时，有色液体流经玻璃管的流线会出现不规则的波浪形，此时流体流动称为转捩流或过渡流（Transition flow），其流动状态如图1-11（b）所示。如果继续增大流速使流体的雷诺数增加，当流体的雷诺数达到一个临界值时，整个玻璃管内的水呈现均匀的颜色，这说明流体质点除了沿管道向前运动外，还存在不规则的径向运动，质点间相互碰撞相互混杂，此时流体的流动称为湍流，其流动状态如图1-11（c）所示。

图1-11 层流、过渡流与湍流的流动形态示意图

由此可知雷诺数的大小决定了黏性流体的流动特性，对于一般的管流，如果流体的雷诺数约低于 2 300，流体的流动为层流。这个临界的雷诺数 Re 称为下临界雷诺数（Lower critical Reynolds number），用符号Rec下表示。如果流体的雷诺数约高于13 800，流体的流动将完全转换成湍流，这个临界的雷诺数Re称为上临界雷诺数（Upper critical Reynolds number），用符号Rec上表示，而流体的雷诺数如果在下临界雷诺数与上临界雷诺数之间，流体的流动为转捩流或过渡流。黏性流体的流动形态判定的准则列举如下。

① 层流流场的判定：若 0 ＜ Re ＜ Rec下，则流体的流动为层流。

② 过渡流场的判定：若 Rec下＜ Re ＜Rec上，则流体的流动为过渡流。

③ 湍流流场的判定：若 Re＞Rec上，则流体的流动为湍流。

通常说的临界雷诺数指的是下临界雷诺数，而对于圆形管流，如果流体的雷诺数低于2 300，可以直接将管内流体的流动形态判定为层流，此时雷诺数Re计算公式中使用的特征速度是圆管横截面上的平均速度。

【例1-11】

假设水在内径 d＝8 mm的管中流过，其平均流速为 V＝0.3 m/s，已知水的动力黏度为μ水=0.001 5 kg/m·s 与水的密度为 ρ水=1 000 kg/m3，又知其临界雷诺数 Rec水=2 300，试判断水在圆管内的流动形态。

【解答】

（1）由题干可知，圆管的特征长度 L 为圆管的内径 d＝80 mm，水在圆管内的临界雷诺数 Rec水=2 300。

（2）雷诺数的计算公式为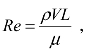所以水在圆管内流动的雷诺数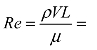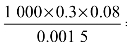= 1 600。

（3）流体流动形态依据雷诺数Re的判定准则，如果 Re＜Rec，流动形态为层流，因为水在圆管内流动的雷诺数小于临界雷诺数，所以水在圆管内流动形态为层流。