通过ADAMS软件提供的图形接口模块，将三维实体造型软件UG中建立的机构三维模型导入到ADAMS软件中的。考虑到所关心的问题和仿真的方便，对操作机构作适当简化后，用ADAMS软件包建模。约束关系的添加要充分考虑实际操作机构中可能存在的约束，遗漏任何一个约束关系都会严重影响到输出结果。3）仿真过程的控制 在ADAMS软件中，为了实现对仿真过程的控制，需要添加传感器来控制仿真过程的自动终止。......
2023-06-15
频率动态仿真误差模型的建立与优化
【摘要】：基于上述定义的频率动态轨迹的特征指标，建立误差模型函数。依据所研究的频率动态问题，分别在每组确定的系统参数下，首先选取若干个有实际参考意义的频率实测轨迹；其次利用电力系统仿真软件仿真得到频率仿真轨迹；然后通过上述已建立的单功率脱落事件下的误差模型计算误差值，并对这些样本进行两两比较，形成判断矩阵；最后通过对判断矩阵进行求解，得到各个样本的权重系数。
电力系统动态仿真精度评价即在电力系统仿真结果中，通过把仿真轨迹与实际轨迹相比较以及判断两轨迹之间的差异是否在规定的范围内来校验证模型的有效性，从而来判定此仿真模型是否真实地反映实际系统的运行情况[12]。本节为使实测轨迹与仿真轨迹的比较有一个量化的标准，建立一个精度评价体系，即仿真误差模型，以便对仿真精度以及轨迹误差进行评价。
1.单一功率脱落事件下的误差模型
为了评价实测轨迹与仿真轨迹之间的差异，在分析电力系统频率动态过程特点的基础上，定义了如下几个体现频率动态轨迹特征的指标（图7.3）：
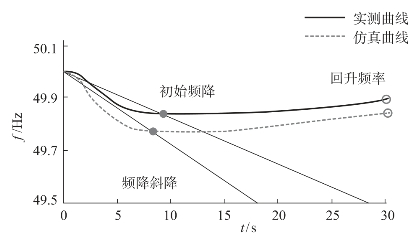
图7.3 仿真轨迹和实测轨迹特征指标示意图
（1）初始频降：指当故障发生后，频率下降到最低值与原稳态频率的差值。该特征量表征了电网事故后频率下降的严重程度；其变化直接影响到频率实测轨迹与仿真轨迹之间的接近程度，即图7.3中黑色圆圈点处频率值与起始点的频率值之差值。
（2）频降时间：指频率从初始时刻到达最低频率值的时间，即到达初始频降的时间。该特征量反映了系统一次调频应对事故后系统频率下降的能力。
（3）频降斜率：指频率从初始时刻下降到初始频降的曲线斜率。如图7.3中直线所代表的斜率。
（4）回升频率：指频率从初始频降上升到的最大值。该特征量表征了电网事故后，频率的恢复特性。如图7.3中白色圆圈点处频率值。
基于上述定义的频率动态轨迹的特征指标，建立误差模型函数。首先建立如下差值函数：
（1）频率轨迹最大差值：频率仿真曲线和实测曲线在时间轴上的最大差值。
（2）频率轨迹平均差值：频率曲线所有时间点上频率仿真轨迹和实测轨迹频率差值的均方差。
（3）频降斜率差值：为仿真轨迹频降斜率和实测轨迹频率斜率差值的绝对值。
（4）回升频率差值：为频率仿真轨迹和实测轨迹回升频率差值的绝对值。
（5）初始频降差值包括两个内容，一个是实测频率轨迹初始下降到最低点对应时刻的频率差值；另一个是仿真频率轨迹初始下降到最低点对应时刻的频率差值。为保证频率实测轨迹频降最低点略高于仿真轨迹，定义差值函数Δf为
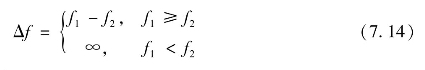
式中，f1为实测频率值；f2为仿真频率值。
通过以上分析得出某一故障条件下的频率实测轨迹和仿真轨迹的误差评价函数，如式（7.15）所示：
式中，fe为误差评价函数；T1为初始频降差值；T2为频降斜率差值；T3为回升频率差值；T4为频率轨迹最大差值；T5为频率轨迹平均差值；λ为相应差值函数在误差评价函数中的权重系数。
各差值函数的权重系数取值可以根据调整的要求而定。初始频降差值、频降斜率差值表征了频率动态轨迹从事故后到频率下降到最低点时一段时间内的动态特性差异；回升频率差值表征了频率经过回升、恢复之后的差异；而频率轨迹平均差值表征了频率轨迹的整体差异程度；频率轨迹最大差值表征了研究时间段内某一时刻频率的最大差异。一般而言，初始频降差值、频降斜率差值和回升频率差值决定了轨迹的主要形状，应赋予较大的权重；其他所占权重略小。
2.多个功率脱落事件下的误差模型
在研究实际电网频率仿真参数修正的过程中，常常可以获取多个实际电力系统功率脱落事件的实测频率轨迹。用多个实测样本来对频率仿真曲线进行校正，可以进一步提高频率仿真的准确度。然而这些功率脱落事件发生的时间不同，故障位置不同，故障的严重程度也互不相同，因而作为频率仿真轨迹的校正样本，它们的参考价值也不同。下面基于层次分析法，来衡量各个实测频率样本的参考价值，进而建立具有多个系统实测频率曲线条件下的误差评估体系，用于综合评价系统频率仿真的准确度。
（1）层次分析法的原理：层次分析法首先把决策问题按照评价准则直至具体的备投方案的顺序分解为总目标和各层次子目标，然后建立判断矩阵，并求得特征向量，进而转化为权向量，也就是各要素对其相应上层要素的影响权重，最后通过求得权和来判定各候选方案对总目标的影响。
（2）基于层次分析法的多个功率脱落事件下的误差模型。
上述层次分析法为我们提供了一种根据比较而确定多个比较对象权重系数的数学方法。依据所研究的频率动态问题，分别在每组确定的系统参数下，首先选取若干个有实际参考意义的频率实测轨迹；其次利用电力系统仿真软件仿真得到频率仿真轨迹；然后通过上述已建立的单功率脱落事件下的误差模型计算误差值，并对这些样本进行两两比较，形成判断矩阵；最后通过对判断矩阵进行求解，得到各个样本的权重系数。所以当具有多个实际电力系统功率脱落事件下的实测频率轨迹时，需要分别在每组确定的系统参数下，计算相对每个样本曲线的误差值，而每个样本曲线的下属因数（误差值）对上层因数（总误差值）的影响力（权重）可以由判断矩阵直接确定。通过权重系数，可以得到具有多个系统实测频率曲线条件下的误差评估体系，即在每组参数下，对多个功率脱落事件的实测轨迹和仿真轨迹进行上述误差计算，加权相加后作为多个功率脱落事件仿真轨迹和实测轨迹的误差值；计算公式如式（7.16）所示：
式中，Fe为在一组确定的系统频率仿真参数条件下，多个仿真轨迹和实测轨迹的误差之和；fem为第m个样本的误差值；m为样本的个数；E为各个样本的权重系数。
有关交直流混合电网计算分析方法的文章
- 详细阅读
-
建立仿真模型的子模块：优化方案详细阅读
图5.2所示为本次仿真使用的偏心轴转角子模型。具体的方法已在5.1.2节中详述，此处MATLAB/Simulink模型将式和式整合，并表达成图5.4所示模型进行计算：图5.2偏心轴转角子模型2.工作室容积子模型转子发动机在工作时，工作室容积变化规律如式（5.9）所示，在发动机基本参数确定之后，它仅是偏心轴转角的函数。......
2023-06-23
-
COMSOLMultiphysics仿真模型详细阅读
COMSOL Multiphysics对于不同案例的具有类似的建模流程，以流体流动模块中的CFD建模为例，可以总结为以下几个步骤。第2步：构建几何模型对于结构比较简单的几何模型，可以采用COMSOL Multiphysics中的“几何”功能模块建立模型；对于结构相对复杂的对象，可以先采用AutoCAD等专业几何设计软件进行设计，再导入COMSOL Multiphysics。对于不太复杂的几何模型，COMSOL Multiphysics近年来的版本都有较好的自适应划分策略。......
2023-11-03
-
仿真模型的建立及分析结果详细阅读
图3-25 三角形隶属度函数模糊控制规则是模糊控制的核心，因此，如何建立模糊控制规则成为一个十分关键的问题。根据表3-3所示参数，由式可得D0=0.24；由式可得x0=[0.11573600]T；由式可得图3-28 模糊控制器输出曲线图3-28 模糊控制器输出曲线图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数取正定矩阵取正定矩阵根据实验取定根据实验取定具体仿真结果如下：1）图3-30所示为无滤波器的情况下电网电流波形。......
2023-06-23
-
建立操作机构仿真模型的方法与步骤详细阅读
建立操作机构仿真模型的最简便的方法是从常用的三维实体造型软件中导入，如从SolidWorks、UG和Pro/E等建立的实体模型完整地导入到ADAMS软件，中间文件格式最好的是Parasolid，以*.x_t和*.xmt_txt文件名导入，断路器操作机构的结构比较复杂。考虑到所关心的问题和仿真的方便，对其作适当简化，将从UG等三维软件导入的低压塑壳断路器操作机构和触头系统的模型进行了删减，在ADAMS/View中重新建立了关键构件的模型，其主要由连杆机构组成。......
2023-06-15
-
建立综合优化调度评估模型详细阅读
本节将运用赋权重的方法考虑各方面约束，以防洪、发电、航运、泥沙为主要优化目标，建立综合优化调度方案评估模型，为三峡水库选定优化调度方案提供决策支持。......
2023-06-21
-
全沙数学模型的建立与优化详细阅读
10.4.2.4沉降系数确定图10-16航道疏浚深度与悬沙沉降系数的关系在悬沙不平衡输沙方程和河床变形方程式中，沉降系数α 对河床冲淤强度有较大影响。......
2023-06-22
- 详细阅读
相关推荐