电压静态稳定性计算与负荷增长方式、电网运行方式和发电机功率增长方式、发电方式和潮流断面增长方式等因素密切相关。本节结合电网运行特点和高压直流输电系统运行特点，在不同的视角下进行交直流电网的电压稳定裕度计算。......
2023-06-29
连续型潮流计算的方法及应用
【摘要】：首先介绍纯交流系统连续型潮流计算方法的原理和步骤[1～3]。图5.1所示为连续型潮流计算法的示意图，该算法主要有4个步骤：参数化、预测、校正及步长控制。
首先介绍纯交流系统连续型潮流计算方法的原理和步骤[1～3]。图5.1所示为连续型潮流计算法的示意图，该算法主要有4个步骤：参数化、预测、校正及步长控制。算法的参数方程和校正过程不尽相同，步长控制也可变化。本书采用改进局部参数法，自适应控制步长求取P-V曲线。
图5.1 连续潮流法计算过程示意图
连续潮流法的基本方程简单描述如下：
式中，λ为发电机和负荷增长参数，即负荷因子，表示系统的负荷水平；x为n维状态变量，x=[U θ]T；f和g为n维函数变量，b为n维常数变量，表示负荷增长方向，其形式为：b=[P1 d，…，Pid，…，P（n-1）d，…，Q1d，…，Qmd]T。
1.参数化
参数化始终贯穿于连续潮流计算中，该方法与预测校正环节需要对方程进行参数化处理。参数化的过程主要是构建一个补充方程确定曲线上单个解，使得下一个解或上一个解可以定量化。该方程形式上存在差别，或描述超平面或描述超曲面，因此构成各类参数化方法。所构造的超平面或超曲平面的焦点即为所求的确定解。预测过程中的切线预测方法应用参数化，校正过程的计算亦同样需应用参数化方法。预测和校正虽然具有不同的表现形式，且相互独立但是两者又具有一定的联系。选择参数化方法必须合理才能使预测准确，校正快速，从而连续潮流顺利进行。
局部参数化选用控制参数λ或状态向量x的其中任意一个分量使曲线参数化，步长表示为Δλ或Δxk。局部参数化方法自动调整变换参数，即以解向量中变化最快的分量作为局部参数的参数选择策略。在预测-校正的过程中，上一步求得的解向量将作为下一步参数的依据，上一过程的计算结果可以指导下一步的预测校正计算。
2.预测
预测的目的是找出下一个解的近似值，为校正环节的牛顿迭代计算提供初值，预估的结果直接关系到连续潮流的鲁棒性以及计算效率。本书预测方法是切线预估法，该法方法较简单，只需要计算状态变量和负荷参数的微分，如式（5.2）：
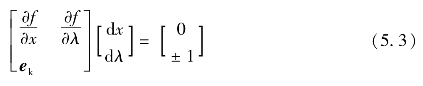
上文的局部参数法中提到，选定切向量（dx、dλ）中的某一个分量为±1，而这个选定的分量即连续参数。潮流方程转变成另一种形式，如式（5.3）：式中，ek表示除第k个元素为1外其余元素都为0，与方程组维数匹配的行向量。首先在初始计算时，连续参数选定为负荷参数λ，且该相应分量设置为+l。往后的预测计算，选将切向量中分量绝对值最大的状态变量（即变化速度最快的分量）为连续参数[3]，其斜率符号对应于切向量中该分量的符号。
利用求得的切向量按下式解得预估计算求解：
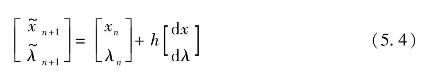
式中，xn、λn为当前点；
为下一点的预测值；dx、dλ为当前点的梯度；h为预测步长因子（选择步长需满足预测得到的解在校正环节可以收敛）。
3.校正
校正环节需要用到预估得到的近似解
作为初值。参数化方法在校正环节和预测环节中略有差别。在原始潮流方程（5.1）基础上联立一个方程，得到新的增广方程：
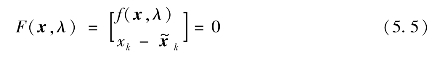
式中，xk为当前点的连续参数，联立一个方程后不能改变临界点增广雅可比矩阵非奇异性。此时第i次迭代系统的修正方程如式（5.6）所示，求解就可得到变量x的值。
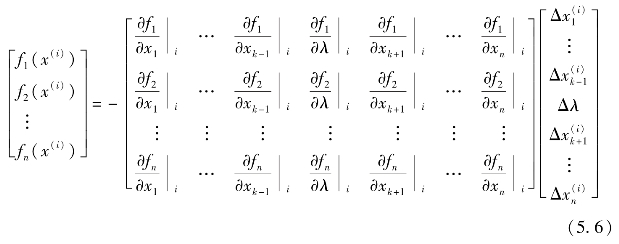
4.步长控制
步长控制对潮流计算精度和结果至关重要。如果选取较大的步长，虽然可以提高计算效率，但是连续潮流参数的误差在传递过程会增大，容易使校正环节在临界点附近潮流解不存在（校正曲线与解曲线的交点不存在）或是首先得出的预估潮流初始值偏差很大，造成校正过程无法正常进行，且系统极限点不能准确求得。如果采用较小的步长，虽然计算精度高且收敛性好，但是计算时间过长[2]。结合步长控制的上述特点，本书采用的步长策略是：先取步长h为较大值，比较每次校正过程中所需的迭代次数，当某次校正过程中潮流计算迭代次数超过上次迭代次数的2倍时，返回到上次潮流计算求得的解，将步长减半重新校正。重复此过程直到校正过程收敛速度较快为止。该步长策略优点是在曲线的“平滑”区迭代计算较少，在“陡峭”区，自动步长减小，提高精确度。
5.到达临界点的判据
连续潮流计算的临界状态以负荷参数的切向量为判据。由于λ的分量dλ在临界点时刚好无变化，可以将dλ=0作为临界点判据。当然dλ的绝对值只要小于一个很小的正数（一般可选为10-3）则认为系统达到了稳定极限。
有关交直流混合电网计算分析方法的文章
- 详细阅读
-
改进连续潮流法的原理优化详细阅读
对上式进行线性变换可以得到式中，为线性变换后所得系数矩阵的子矩阵。将上式拆解为预测计算的直流系统约束方程和交流系统约束方程分别如下：同理，在进行校正计算时，泰勒级数展开直流子系统潮流方程式并忽略二次以上高阶项后，得到校正计算的修正方程：同理，对上式进行线性变换，消去系数矩阵可以得到式中，Ax和At为线性变换后所得系数矩阵的子矩阵；Cx和Ct为线性变换后得到的列向量的子向量。......
2023-06-29
- 详细阅读
-
连续激光切割的特性及应用详细阅读
高的切割速度1200W的CO2激光切割2mm厚低碳钢板的切割速度达到0.1m/s，切割5mm厚有机玻璃的切割速度0.2mm/s；激光切割钢板生产率达到冲模下料的30%左右。试验设备和材料 其试验设备采用波长为10.6μm、功率为4kW的快速轴流CO2激光器，光束聚焦使用125mm的透镜。......
2023-06-26
-
闭式网潮流分布计算方法详细阅读
在求出闭式网络中的初步功率分布后，还必须计算网络中各段的电压和功率损耗，方能获得潮流分布计算的最终结果。从闭式网络的初步功率分布可以看出，某些节点的功率是由两侧向其流入的，这种节点称为功率分点，并用符号“▼”标出，如有功、无功功率分点不一致，则以“▼”、“▽”分别表示有功功率、无功功率分点。......
2023-06-15
-
牛顿-拉夫逊法在潮流计算中的应用详细阅读
用牛顿—拉夫逊法进行潮流计算时，节点导纳矩阵的形成、平衡节点和支路功率计算都和运用高斯—塞德尔法时相同，区别仅在于迭代过程。根据式可得式即是用牛顿—拉夫逊法潮流计算时的功率方程。图4-4是牛顿—拉夫逊法潮流计算的流程图。给定值为容许误差ε＝10－5试用牛顿—拉夫逊法计算潮流分布。......
2023-06-15
-
图形面积计算方法及应用详细阅读
我们如果只凭直观感受进行判断,那么很可能产生错觉或错误的判断,我们把看上去的情况和实际有偏差的图形,称之为错视图形．知能概述面积是平面几何中一个重要概念,计算图形面积是平面几何中最基本的问题之一,常用的计算方法有:和差法、运动法、等积变形法．面积的计算主要是求一些非常规图形的面积,非常规图形面积的计算往往可转化为常规图形面积的计算．在转化的过程中,常用到恰当连线、图形割补、等积变形、线段比与面积比......
2023-08-13
-
差分光流计算的方法及应用技巧详细阅读
本章方法基于第6章描述的差分图像，前述的光流计算方法用于差分图像会有一些限制，例如：差分图像是二值图像，所有的前景灰度和所有的背景灰度均相同，在灰度匹配时产生误差的可能性增加了。差分图像中前景成分很少，利用全局计算方法运算浪费严重。在前景范围内平滑光流向量。图7.2差分图像序列（第1行）、利用Horn-Schunck方法计算的光流场序列（第2行）和用新方法计算的光流场序列（第3行）......
2023-06-16
相关推荐