粒子群优化算法,是Eberhart和Kennedy[118]提出的一种基于群体智能的优化算法,它是受鸟群和鱼群群体运动的行为方式启发而得到的。这些算法从不同方面对粒子群优化算法进行了改进,不同程度地提高了优化算法的收敛速度和精度,但是效果不是很理想。高鹰等人把混沌思想引入粒子群优化算法中,提出了混沌粒子群优化算法[127-129],取得了良好的效果。因此,本书拟采用混沌粒子群优化算法对风—光—抽蓄复合发电系统进行优化配置。......
2025-09-29
粒子群优化算法的原理和应用
【摘要】：粒子群优化算法的基本思想：PSO中每个优化问题的潜在解是搜索所在空间中的一个粒子，所有的粒子都会有一个对应的函数值来衡量每个粒子解的优越程度，每个粒子还会有一个对应的速度来决定自身飞翔的距离和方法，最终可以实现从全局域内搜索到最优解的目的。
粒子群优化算法（Particle Swarm Optimization，PSO）的基本思想：PSO中每个优化问题的潜在解是搜索所在空间中的一个粒子，所有的粒子都会有一个对应的函数值来衡量每个粒子解的优越程度，每个粒子还会有一个对应的速度来决定自身飞翔的距离和方法，最终可以实现从全局域内搜索到最优解的目的。
PSO算法的初始可行解可以选择一群随机解（粒子），每次迭代过程中，粒子的更新是通过跟踪两个极值来实现：第一是粒子自身寻找个体极值点pbest；第二是整个种群全局极值点gbest，如图4.4所示。假设在一个d维的目标搜索空间中，有m个粒子组成一个群落，其中第i个粒子表示为一个d维的向量
第i个粒子的“飞行”速度也是一个d维的向量，记为
第i个粒子迄今为止搜索到的粒子本身最小适应值对应的个体最优解，记为
整个粒子群在迄今为止搜索过程中的最小适应值对应的全局最优解，记为
在寻找到以上两个最优值时，可以按照如下公式更新粒子本身的速度和距离：
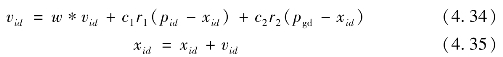
式中，ω为惯性权重，一般情况下ω的初始值一般取为0.9，使其随着算法过程中迭代次数的增加而线性递减至0.4，这样可以使得搜索先全局寻优；c1和c2为加速常数，一般取值为2；r1和r2为在（0，1）范围内均匀分布的随机数。式（4.34）中右边第一部分为粒子的惯性部分，反映了粒子有维持自己先前运动速度的习惯；第二部分为粒子的认知行为，反映了其对自身历史最佳位置逼近的记忆；第三部分为社会部分，反映了粒子间有向群体或邻域历史最佳位置逼近而相互协同合作与信息共享的历史经验[14]。
采用灵敏度分析与粒子群算法相结合的特高压交直流混合电网无功优化计算步骤如下：(https://www.chuimin.cn)
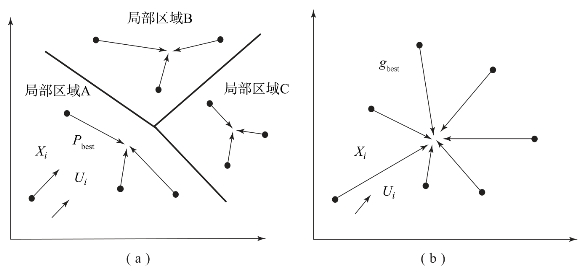
图4.4 粒子群的空间寻优过程
（a）寻优区域；（b）寻优目标
（1）计算高压交直流系统初始潮流和目标函数初值；
（2）计算电压对补偿节点的灵敏度系数，并比较大小；
（3）根据灵敏度系数选择无功调节节点集合；
（4）初始化粒子群体（群体规模为无功调节节点集合变量个数），得到一组初始粒子，即初始解；
（5）计算每个粒子的适应度，即针对每种补偿情况，进行潮流计算，并根据潮流计算结果计算目标函数值；
（6）根据适应度更新pbest、gbest，更新粒子位置速度，得到新的粒子群体，即得到一组新的无功控制集合；
（7）若达到最大迭代次数或目标函数值满足优化要求，停止计算，转入步骤（9）；
（8）重复步骤（5）；
（9）得出优化结果。
相关文章
- 详细阅读
-
DBSCAN算法的原理及优化探究详细阅读
DBSCAN通过检查数据集中每点的Eps邻域来搜索簇，如果点p的Eps邻域包含的点多于minPts个，则创建一个以p为核心对象的簇。DBSCAN迭代地聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并。当没有新的点添加到任何簇时，该过程结束。算法9.3DBSCAN算法输入:数据集D；给定点在邻域内成为核心对象的最小邻域点数:minPts；邻域半径:Eps；输出:簇集合。标记所有对象为unvisited。重复步骤～，直至没有标记为unvisited的对象。......
2025-09-29
-
粒子群算法优化半导体生产调度的关键步骤详细阅读
表6-2每个工序对应工件的优先水平表6-3某一粒子编码在粒子算法求解调度问题中， 一个粒子代表一个调度方案。粒子的维数等于每个工件经过加工环节数量之和。在计算初始时刻， 粒子的初始种群和初始速度都是随机产生的。位置的先后也是调度方案中执行生产的先后。粒子算法可以适合大规模的调度研究， 并......
2025-09-29
-
粒子群算法特点及优势分析详细阅读
粒子群算法的优势在于它的算法简单、 易于实现， 可调参数少， 收敛速度快、 求解快， 可以用于大规模的优化模型中； 基于记忆的特点， 可以对以往产生的最优位置进行保存。公式(6-2)表示了粒子的位置是由上个时刻位置与上个时刻粒子的运动所共同影响的。在粒子群算法的整个过程中， 惯性权重w、 r1、 r2 和最大速度Vmax 对算法的搜索能力和性能影响很大。......
2025-09-29
-
工艺的工作原理优化为工艺的原理和作用详细阅读
UASB反应器中废水为上向流，最大特点是在反应器上部设置了一个特殊的气、液、固三相分离系统，三相分离器的下部是反应区。气、液、固的混合液上升至三相分离器内，气体可被收集，污泥和水则进入上部相对静止的沉淀区，在重力作用下，水与污泥分离，上清液从沉淀区上部排出，污泥被截留在三相分离器下部并通过斜壁返回到反应区内。图9-8UASB反应器中沿高度的污泥浓度分布示意图较低水力负荷；较高水力负荷......
2025-09-29
-
反渗透装置的应用和原理详细阅读
目前反渗透装置有板框式、管式、卷式和中空纤维式四种类型。管式装置是把膜浇铸在直径为0.32～2.54cm的多孔支撑管上制成。含盐水由一端流入导流隔网，从另一端流出，透过膜的淡化水沿多孔支撑材料流动，由中间集水管引出。图6-12卷式膜装置示意图中空纤维式装置是把纤维定向平行放置于开孔的中心管上而成。该装置特点是，膜的装填密度最大而且不需外加支撑材料。表6-5各种形式反渗透器的性能比较①①原水5000mgNaCt/L。......
2025-09-29
- 详细阅读
-
自适应滤波算法及其应用详细阅读
衡量一种自适应算法的优劣一般有两个衡量标准，即参数收敛速度和收敛以后的稳态误差。这种情况下自适应滤波器大部分时间处在未收敛状态，收敛后的精度就显得不太重要。这种算法常采用最小二乘准则即把块内的误差平方求和后要求其和最小，自适应算法的速度和精度的矛盾可以在分块算法中得到体现。......
2025-09-29
相关推荐